考虑能耗指标的双层自动化立体仓储系统布局研究
马云峰 赵佳伟 胡依娜 熊依蓓 卢阳


摘 要:为解决仓储系统运行过程中能源消耗过大的问题,针对双层自动化立体仓库进行了能耗分析,建立了双层仓储系统存储、检索任务时间模型以及考虑物品自重的穿梭车(提升机、电梯)运动能耗模型,并利用仿真实验研究了仓库中自动小车及提升机的速度、加速度,货架布局对于仓库运行能耗、吞吐量的关系和影响。实验结果显示增加穿梭车速度、加速度都会提升系统吞吐量,速度对吞吐量的提升更大;增加电梯加速度、速度会适当降低能耗。达到吞吐量500条件下,新的系统布局可以降低20%左右的能耗并提升2.7%的吞吐量,帮助物流企业建立更加合理的仓库布局设计,从而减少存储和检索过程中的能源消耗。
关键词:双层自动化立体仓储系统;时间模型;能耗模型;仓储系统布局
中图分类号:F253.9文献标志码:ADOI:10.13714/j.cnki.1002-3100.2024.10.001
Abstract: In order to solve the problem of excessive energy consumption during the operation of the storage system, an energy consumption analysis was conducted for a double-layer automated three-dimensional warehouse. A time model for storage and retrieval tasks in the double-layer storage system was established, as well as a motion energy consumption model for shuttle cars (hoists, elevators) considering the weight of the items. Simulation experiments were conducted to study the relationship and influence of the speed and acceleration of automatic carts and hoists, and shelf layout on the energy consumption and throughput during warehouse operation in the warehouse. The experimental results show that increasing the speed and acceleration of the shuttle car will improve the system throughput, and speed has a greater impact on the throughput; increasing elevator acceleration and speed will appropriately reduce energy consumption. Under the condition of reaching a throughput of 500, the new system layout can reduce energy consumption by about 20% and increase throughput by 2.7%, helping logistics enterprises establish more reasonable warehouse layout design, thereby reducing energy consumption during storage and retrieval processes.
Key words: double-layer automated stereoscopic storage system; time model; energy consumption model; warehouse system layout
0 引 言
随着电商与现代物流业[1]的高速发展,企业对仓储系统的性能和能耗也提出了更高的要求[2]。传统的堆垛式仓库已无法满足高吞吐量、低能耗的要求。工业4.0[3]、智能化的高速发展趋势,促使各类自动化小车、提升机被运用到仓储系统中,不同种类的自动化仓储系统应运而生。
针对仓储系统的吞吐量性能,国内外学者进行了广泛的研究,且结合实际应用提出了不同的优化方式。Tappia等[4]构建了半开放排队网络模型估计系统性能,给出最佳深度/宽度比,以最大限度地减少单层系统中的预期吞吐时间。Ekren等[5]研究了基于分类存储策略下基于穿梭车的存储系统最佳货架设计。Zhao等[6]提出了一个高效的仿真模型,可以针对不同的机架配置进行自动重新设计,针对包含81种不同货架类型的多电梯层级进行了仿真案例研究,找到了最佳货架设计。
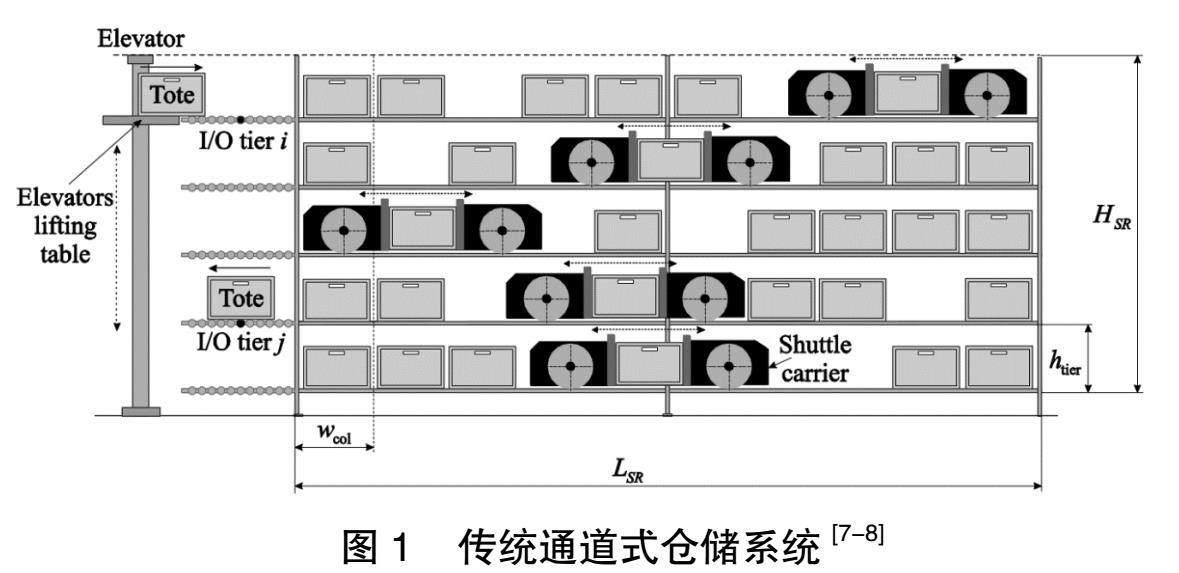
图1为传统通道式仓储系统,因其具有建设成本低、结构简单等优势,在物流企业中被广泛应用[7-8]。但由于其单电梯结构,穿梭车数量远大于电梯数量,导致货物上下运输过于依赖电梯,极易出现货物在缓冲区等待电梯,导致系统拥堵的情况。图2为双层自动化立体化存储系统,Lerher等[9]设计并验证了其吞吐量优于相同货位的传统通道仓储系统。该系统由上下两层、一台电梯,以及两台拥有提升机的穿梭车组成,其中电梯只在命令处于上层时运行,下层的命令不使用电梯,将系统上下运动分担到穿梭车提升机上,打破了电梯造成的吞吐量瓶颈,从而提升系统的吞吐量。
由于仓储设计不断优化和改善,系统的吞吐量性能不断增加,导致仓储系统的能耗也不断提高,国内外学者对仓储系统能耗问题也进行了研究。张新艳等[10]在前人的基础上,引入了高度因素进行能耗建模,并进行了对比分析。夏绪辉等[11]针对三维路径规划问题,建立了以绿色度最大为目标的优化模型。Liu等[12]探讨了在吞吐量要求下基于穿梭车的存储和检索的环保速度和加速度配置,为具有在双指令循环基础上运行的交叉穿梭机开发了一个能耗模型。Ekren等[13-14]对基于穿梭车的存储和检索系统设计进行了实验研究,以确定影响系统性能指标的重要因素。
上述研究以吞吐量和能耗为目标,为仓储系统布局优化的研究提供了良好的理论基础。本文以双层自动化立体存储系统为背景,研究仓储系统中穿梭车和电梯的速度、加速度对系统能耗和吞吐量的影响,在保证吞吐量的前提下,以降低仓储系统能耗为目标,通过数学分析,并以企业实际数据为基础进行仿真实验,对结果进行处理和分析,找寻最低能耗的仓储系统布局。
1 问题描述
在图2双层自动化立体仓储系统中,上下层各有1个带有独立提升机的穿梭车,在系统的左侧拥有只处理上层命令的电梯。系统接到下层的存储命令时,直接通过下层穿梭车和提升机进行作业,将货物从输入/输出()点运送至指定货位;系统接到上层的存储命令时,电梯先将货物从底层运输到n+1层(n为下层层数),然后穿梭车从输入/输出()点运送至指定货位。检索命令工作原理类似,并且在系统运行中,穿梭车、提升机、电梯可以同时作业。
在该系统中,穿梭车、提升机、电梯的速度和加速度数值会影响系统整体的吞吐量性能和能耗。在加速度和速度不变的情况下,不同的系统层数和列数也会对系统的吞吐量性能和能耗有较大影响。因此考虑通过数学分析,并以企业实际数据为基础进行仿真实验,对结果进行处理和分析。
2 仿真模型(见表1)
2.1 电梯、穿梭车、提升机运动时间计算
如图3所示,穿梭车水平和提升机的上下移动、电梯上下移动均存在两种方式的运动模式,即加速—减速、加速—匀速—减速。因此要计算出两种运动方式的临界距离。
临界距离 (1)
当穿梭车水平移动距离、电梯上下移动的距离、穿梭车提升机上下移动距离小于临界距离时(即加速—减速运动模式),以穿梭机水平移动为例。
总运动时间== (2)
加速运动时间=减速时间= (3)
加速运动移动距离=减速运动移动距离= (4)
当、、大于临界距离时(即加速—匀速—减速运动模式),以穿梭机水平移动为例。
总运动时间+ (5)
加速运动时间t1=减速时间 (6)
匀速运动时间=- (7)
加速运动距离=减速运动移动距离 (8)
匀速运动距离=- (9)
2.1.1 储存命令
物品的目标位置位于内,存储任务不使用电梯E,穿梭车由当前位置移动到点并拾取物品,随后穿梭车向着目标列移动的同时,穿梭车上的升降机带着物品向上移动到目标层,这两种操作同时进行以缩短任务时间提升效率。
+ (10)
为穿梭车移动至点,且提升机移动至最底层所需时间;为穿梭车由当前位置移动到点所需时间;为穿梭车提升机由当前位置移动到底层所需时间; 为穿梭车由点移动至目标列,且提升机移动到目标层所需时间;为穿梭车从点移动到目标列所用的时间;为穿梭车提升机移动到目标层所用的时间;为穿梭车提升机装载物品的时间;为穿梭车提升机卸载物品的时间。
物品目标位置位于level内,物品由电梯E提升至level并放置到缓冲区域,随后由当前层的穿梭车完成储存任务。
++ (11)
+ (12)
为目标物品由电梯运送至层的缓冲区域,并由提升机装载所需时间;为电梯E由当前位置下降至点所用时间(0,已知值);为电梯E从点移动至level(n+1层)所需时间(已知值);为电梯卸载物品所需时间;为电梯装载物品所需时间。
2.1.2 检索命令
目标物品Y位于内,检索任务不使用电梯E,穿梭车及其提升机由当前位置移动到目标物品Y的同一列和同一层,取出目标物品后,提升机向下移动至底层,穿梭机向移动并将物品放置在缓冲位置。
(13)
为穿梭车由当前移动至目标列,且提升机移动至目标层所需时间。
目标物品Y于,检索任务需要使用电梯E,由穿梭车将目标物品放置到缓冲区域后,由电梯E将目标物品移动至。
+ (14)
+ (15)
为目标物品由穿梭车运输至缓冲区,并被装载在电梯上所需时;为电梯E由n+1层下降至第一层的时间(已知);为电梯E由当前位置移动至n+1层的时间(0,或者已知)。
2.2 能耗分析
为穿梭车牵引力,穿梭车的加速度,质量为,货物质量为,摩擦系数,变速旋转质量阻力系数,加速运动距离D1,匀速运动距离,减速运动距离。
2.2.1 穿梭车能耗分析
穿梭车水平加速运动如下。
空载: 。 (16)
满载: 。 (17)
2.78 (18)
穿梭车水平匀速运动如下。
空载: 。 (19)
满载:。 (20)
2.78 (21)
穿梭车水平减速运动如下。
空载:。 (22)
满载:。 (23)
2.78 (24)
2.2.2 穿梭车提升机及电梯能耗分析
以电梯运动为例,穿梭车提升机质量,电梯质量。
向上加速运动(向上减速运动)如下。
空载:。 (25)
满载:。 (26)
2.78 (27)
向上或向下匀速运动如下。
空载:。 (28)
满载:。 (29)
2.78 (30)
向下加速运动(向下减速运动)如下。
空载:。 (31)
满载: (32)
2.78 (33)
3 仿真实验设计
为了找出影响吞吐量、能耗之间的关系,基于第3节中的模型和公式进行了仿真实验。实验设计以单通道、两侧各1 200个货位的双层自动化立体仓储系统为背景(容量Q=1 200*2=2 400),表2列出了系统中其他参数。
针对表3中6种仓储系统布局,穿梭车、电梯速度不同数值总计625个速度剖面进行组合实验(见表4)。在仿真实验中随机生成300个命令,根据仓储货位使用频率,设置第二层货位的存储/检索频率为30%,第一层为70%(其中210个命令在第一层,90个命令在第二层),每种系统布局完成10组实验。
仿真实验通过配置为AMDRyzen5 3500U@2.10 GHz、8.00 GB的windows10、64位的笔记本电脑上进行,其中仿真代码通过PYTHON-3.7.8软件进行编写并进行实验。仿真实验流程如图4所示。
4 实验结果分析
穿梭车、电梯和穿梭车升降机的速度和加速度可能对能耗和吞吐量产生不同的影响。不同仓储系统布局下的能耗和吞吐量对速度和加速度的敏感程度也不同。选用各情况下吞吐量效果最佳的布局进行分析;速度剖面选择穿梭车、电梯的速度、加速度数值均为2,更加符合仓储实际使用情况。
4.1 加速度对系统能耗的影响
在表5速度剖面-实验中,将穿梭车最大加速度amax由1m/s2逐渐提升到3m/s2时,系统吞吐量由480持续增加至542,吞吐量增长率变化在7.03%~12.82%之间;而系统能耗几乎不变,能耗增长率在-0.64%~0.94%之间。这表明增加穿梭车加速度,可以增加系统吞吐量,同时几乎不增加系统能耗。
在表6速度剖面-实验中,将电梯(提升机)最大加速度由1m/s2逐渐提升到2.5m/s2时,系统吞吐量由484持续增加至539,然后在速度剖面略有下降,吞吐量增长率在5.17%~11.24%之间;系统能耗增长率在在-0.95%~3.79%之间,小范围波动。在上述系统布局中,吞吐量先增加后降低,能耗在较小的范围波动变化,在速度刨面配置下,系统吞吐量最高且能耗最低。
4.2 速度对能耗的影响
在表7速度剖面-实验中,将穿梭车的最大速度由1m/s2逐渐提升到3m/s2时,系统吞吐量由354持续增加至579,吞吐量增长率在29.87%~62.12%之间,系统能耗小幅度增加,能耗增长率在0.38%~7.10%之间。这表明增加穿梭车最大速度,可以增加系统吞吐量,但也会导致系统能耗增加。参考图5,在速度剖面-实验中,能耗大幅度增加,能耗增速上升;而吞吐量小幅度增加,增速下降。因此,对于系统吐量要求中等的仓储系统,选择速度剖面更为合适。
在表8速度剖面-实验中,将电梯和提升机的最大速度由1m/s2逐渐提升到3m/s2时,系统吞吐量由378持续增加至552,吞吐量增长率在26.46%~45.90%之间,系统能耗均小幅度下降,能耗增长率在-0.31%~-2.64%之间。这表明增加电梯和提升机的最大速度,可以增加系统吞吐量,同时降低系统能耗。相较于速度剖面、,速度剖面系统的吞吐量大幅度增加,并且能耗也小幅度下降,对于系统吞吐量要求中等的仓储系统,选择速度剖面最佳;对于系统吞吐量要求较高的仓储系统,选择速度剖面最佳(见图6)。
4.3 系统布局与速度剖面的选择
具有不同速度剖面的双层自动化立体存储系统可能具有相同或相似的吞吐能力,但能耗不同。
当仓储系统的速度剖面固定,以速度剖面为例,不同系统布局能耗和吞吐量数值如表9所示。吞吐量要求至少为500订单/小时,24*50、30*40系统布局满足吞吐量的条件,30*40布局下比24*50布局的系统能耗降低20%左右,并提升2.7%的吞吐量,因此选择30*40的系统布局更优。
当仓储系统的布局一定时,以40*30系统布局为例,不同系统布局能耗和吞吐量数值如表10。有16个速度剖面实验达到600吞吐量,速度剖面能耗最低,因此选择剖面最佳(见表10)。
4.4 吞吐量与能耗的关系
图7反映了30*40系统布局下,625个速度剖面的能耗与吞吐量的变化趋势。能耗和吞吐量均呈现周期性变化,且周期性几乎重合;随着吞吐量的增加,能耗也相应增加。因此,认为能耗与吞吐量呈现正相关。
5 结论及展望
在本研究中,开发了一个基于双命令循环的双层自动化立体存储系统的吞吐量、运行时间和能耗计算模型。基于所提出的模型和实际应用的数值实验得出了以下结果。
增加穿梭车加速度,可以增加系统吞吐量,同时几乎不增加系统能耗。增加穿梭车的最大速度,可以增加系统吞吐量,但也会导致系统能耗增加。
增加提升机和提升机加速度,系统吞吐量先增加后降低,能耗在较小的范围波动变化。增加电梯和提升机的最大速度,可以增加系统吞吐量,同时降低系统能耗。
在速度剖面固定时,30*40、40*30的布局的吞吐量相对较高,且能耗相对较低,综合性能最好。
在实验中,随着货架高度不断下降,完成300个随机命令的时间先下降后增加,在30*40、40*30的货架布局时,实验输出的时间数值最小,系统的单位时间吞吐效率最高。上下层的命令比例(高频货物存放的比例),对系统的效率有巨大的影响。当上层与下层的命令完成时间越接近时,系统整体的效率越高。在上层∶下层命令比例为4∶6的实验中,在30*40、40*30的货架布局中,上层时间与下层时间的比值在1附近浮动,因此这两种货架布局的系统吞吐效率是相对最优。
随着货架高度不断下降,完成300随机命令的能耗不断下降,在40*30、50*24、60*20货架的局部时,实验输出的能耗数值相对其他布局要小,且下降幅度变缓。上下层的命令比例,对系统的能耗有巨大的影响。当上层与下层的能耗越接近时,系统整体的能耗也在下降。
参考文献:
[1] 罗亚楠,邵波,张生,等.“一带一路”倡议下对我国跨境电商物流业发展的研究和建议[J].中国航务周刊,2022(50):57-59.
[2] BOYSEN N,DE KOSTER R,WEIDINGER F.Warehousing in the e-commerce era: A survey[J].European Journal of
Operational Research,2019,277(2): 396-411.
[3] 王雪琳.工业4.0和智能物流[J].珠江水运,2016(10):88-89.
[4] TAPPIA E,ROY D,DE KOSTER R,et al.Modeling,analysis,and design insights for shuttle—based compact storage systems[J].
Social Science Electronic Publishing,2018,51(1):269-295.
[5] EKREN B Y,SARI Z,LERHER T.Warehouse design under class-based storage policy of shuttle-based storage and retrieval
system[J].IFAC-PapersOnLine,2015,48(3):1152-1154.
[6] ZHAO Ning,LUO Lei,ZHANG Saipeng,et al.An efficient simulation model for rack design in multi-elevator shuttle-based
storage and retrieval system[J].Simulation Modelling Practice and Theory,2016,67:100-116.
[7] LERHER T,EKREN Y B,SARI Z,et al.Simulation analysis of shuttle based storage and retrieval systems[J].International Journal of
Simulation Modelling,2015,14(1): 48-59.
[8] LERHER T.Travel time model for double-deep shuttle-based storage and retrieval systems[J].International Journal of Production
Research,2016,54(9): 2519-2540
[9] LERHER T,FICKO M,PAL?I? I.Throughput performance analysis of Automated Vehicle Storage and Retrieval Systems with
multiple-tier shuttle vehicles[J].Applied Mathematical Modelling,2021,91:1004-1022.
[10] 张新艳,邹亚圣.基于新布局模式的仓库能耗问题建模[J].机电一体化,2019,25(6):41-47.
[11] 夏绪辉,朱强,王蕾,等.考虑时间和能耗的立体仓库三维空间路径优化[J].武汉科技大学学报,2018,41(6):465-472.
[12] LIU Ziwei,WANG Yanyan,JIN Mingzhou,et al.Energy consumption model for shuttle-based Storage and
Retrieval Systems[J/OL].Journal of Cleaner Production,2021,282:124480.[2023-08-01].https://doi.org/10.1016/j.jclepro.2020.124480.
[13] EKREN B Y.A simulation-based experimental design for SBS/RS warehouse design by considering energy related performance
metrics[J/OL].Simulation Modelling Practice and Theory,2020,98:101991.[2023-07-25].https://doi.org/10.1016/j.simpat.2019.101991.
[14] EKREN B Y,AKPUNAR A.An open queuing network-based tool for performance estimations in a shuttle-based storage and retrieval system[J].Applied Mathematical Modelling,2021,89:1678-1695.??

