高速公路平面坐标系建立问题的探讨

摘 要：【目的】解决高速公路平面坐标系的建立问题，提高平面坐标系的测设精度，有效确保工程建设质量。【方法】根据高斯正形投影误差计算公式和误差限差理论，分析高斯正形投影误差的组成及各部分的大小，利用平移量计算高速公路平面坐标系的中央子午线和投影高，将标准坐标系下控制点坐标转化为新坐标系下坐标。【结果】对新坐标进行精度验算，两点间通过坐标反算获得的平距与实测平距的差值处于允许范围之内，建立了满足高速公路工程精度需要的新坐标系。【结论】实践表明：高速公路平面坐标系可根据计算所得的中央子午线和投影高来建立具有抵偿高程面的任意带高斯正形投影平面直角坐标系，且新建平面坐标系下各控制点的变形量都能满足规范精度与设计要求。

关键词：平面控制测量；任意带；高斯投影；高程投影面

中图分类号：P217      文献标志码：A     文章编号：1003-5168（2024）08-0066-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.08.013

Exploration Problems of Establishing the Plane Coordinate System for

Highways

HU Yi

（Sichuan Transportation Survey and Design Research Institute Co.， Ltd.， Chengdu 610017， China）

Abstract： [Purposes] This paper aims to solve the problem of establishing a plane coordinate system for highways， improve the measurement accuracy of the plane coordinate system， and effectively ensure the quality of engineering construction. [Methods] Based on the calculation formula and error tolerance theory of Gaussian conformal projection error， the author analyzed the composition of Gaussian conformal projection error and the size of each part. Using the translation amount， the central meridian and projection height of the highway plane coordinate system were calculated， and the control point coordinates under the standard coordinate system were transformed into coordinates under the new coordinate system. [Findings] The accuracy of the new coordinates was checked， and the difference between the horizontal distance obtained through coordinate inverse calculation and the measured horizontal distance between the two points was within the allowable range. A new coordinate system was established to meet the accuracy requirements of highway engineering. [Conclusions] Practice has shown that the plane coordinate system of highways can be established into any Gaussian orthomorphic projection plane rectangular coordinate system with compensated elevation plane based on the calculated central meridian and projection height， and the deformation of each control point under the new plane coordinate system can meet the specification accuracy and design requirements.

Keywords： plane control survey; arbitrary band; gaussian projection; elevation projection surfaces

0 引言

随着我国高速公路建设由平原丘陵地区向山区不断延伸，工程建设技术要求不断提高，新兴勘察技术不断地被应用，国家统一的3°带高斯正形投影平面直角坐标系［1］难以满足现阶段高速公路建设的需要，特别是特大桥、特长隧道的投影变形量应远远小于基本变形量25 mm/km［2］，因此，在高速公路初步设计阶段，结合线路走向、线路设计高度、沿线重要构筑物尺寸等，建立合理有效的线路平面坐标系，以控制投影变形对工程建设的影响，从而保证工程各阶段的顺利实施。

具有抵偿高程面的任意带高斯正形投影平面直角坐标系不仅能高效控制投影变形，还能与3°带高斯正形投影平面直角坐标系建立联系，被广泛应用于工程建设各个阶段。通过分析投影变形引起的误差，可以建立满足项目需求且具有抵偿高程面的任意带高斯正形投影平面直角坐标系［3-6］，从而作为高速公路的平面坐标系。

1 投影变形分析

地球形状是椭球形，是一种立体的形状，应使用三维坐标才能对其进行表达。然而，在工程建设中常使用二维坐标。为了将三维坐标转化为二维坐标，通常使用高斯正形投影将椭球面上的元素投影到平面上。在这个过程中，角度不发生变化，但长度会发生变形。这个变形量的大小由实测边长归算到椭球面上时产生的变形量和椭球面上边长归算到高斯投影面上时产生的变形量共同决定［7］。可由式（1）、式（2）、式（3）求得。

[△s1= -sHmR] （1）

[△s2≈s0y2m2R2m] （2）

[△s=△s1+△s2≈ y2m2R2m-HmRs]   （3）

以上式中：[Hm]为归算边高出参考椭球面的平均高度，m；[s]为归算边的长度，m；[R]为归算边方向参考椭球法截弧的曲率半径，m；[ym]为归算边两端点横坐标平均值，m；[Rm]为参考椭球面平均曲率半径，m；[s0]为投影到参考椭球面上的归算边长度，m，[s0=s+△s1]。

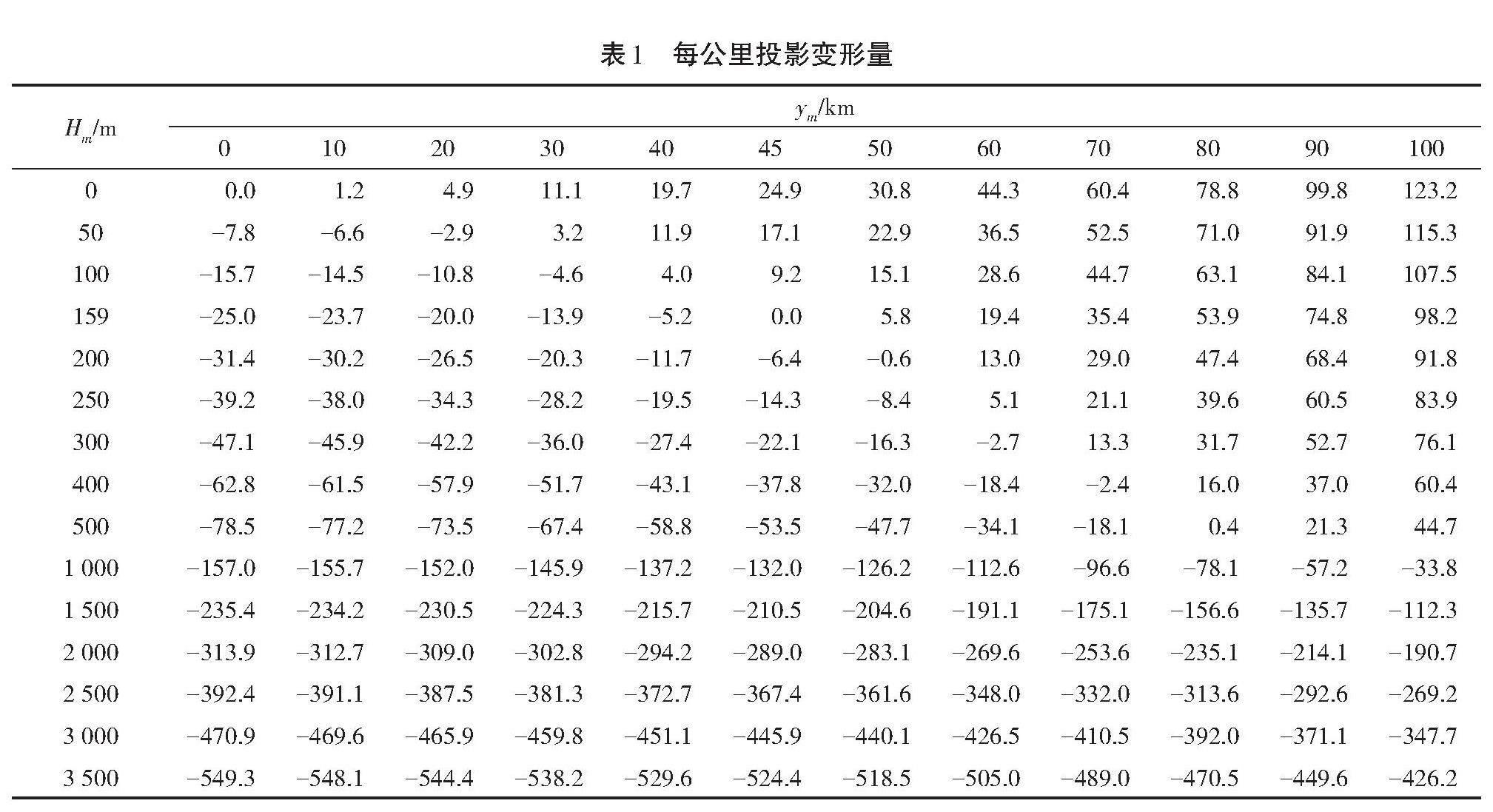
当取[Rm]≈R=6 371 393 m时，根据式（3）计算可得每公里投影变形随[ym]和[Hm]变化的情况，见表1。

由式（1）、式（2）、式（3）和表1，可以归纳出高斯投影变形有以下特征：①在将地面实测长度归算至参考椭球体面上时，长度总是变短。变形量的大小与归算边相较于参考椭球面的平均高度的差值呈正相关。②椭球面上长度归算至高斯面上，长度总是变长，距离中央子午线越远变形越大。③以上两种变形符号相反，且在一定的范围内，可以实现两种变形的相互抵消。

2 建立原理

高速公路工程是典型的线性工程，呈带状，沿线地形地貌变化多端，特别是线路呈东西走向、横跨国家统一3°带或者处于地形起伏变化巨大的地区时，投影变形量几乎无法满足25 mm/km的基本要求。因此，需要根据具有抵偿高程面的任意带高斯正形投影平面直角坐标系的特性，选择合适的中央子午线、投影面高度，建立高速公路平面坐标系。结合投影变形计算公式，满足投影变形要求的条件式可以表示为式（4）。

[|y2m2R2m-HmR|≤140 000]        （4）

式（4）展开后得式（5）。

[ y2m2Rm-R4 000≤Hm≤y2m2Rm+R4 000]         （5）

式中：[R]、[Rm]近似相等。

3 平面坐标系的建立

本研究以某全长约60 km、呈南北走向，且全线处于国家3°带坐标系第35带中的高速公路工程为实例，结合具有抵偿高程面的任意带高斯正形投影平面直角坐标系的建立原理，建立高速公路工程的平面坐标系。

3.1 控制点埋设测量及变形验算

根据该高速公路初步设计阶段基本稳定的线路平面及设计高度，依据相应规范，在路线沿线埋设90个控制点。利用4台GNSS接收机，采用边连式的方式对控制点进行观测，并与3个国家点进行联测，以获得90个控制点在国家3°带高斯正形投影平面直角坐标系中的坐标。依据式（3）检验各控制点处的每公里投影变形量，最小变形量为-60.6 mm/km，最大变形量为-106.9 mm/km。由于没有控制点满足25 mm/km的投影变形要求，因此无法直接使用国家3°带高斯正形投影平面直角坐标系作为线路平面坐标系，需要另行设计。

3.2 绘制[ym—Hm]断面图

根据各控制点的[ym]值和[Hm]值，绘制控制点[ym—Hm]断面。为了直观显示各控制点处的投影变形量与目标量之间的差距，根据式（5）绘制满足25 mm/km要求的投影变形区域界限，如图1所示。

图1中满足25 mm/km投影变形要求的区域位于两条二次曲线之间，所有控制点的断面均不满足投影变形要求。为了使断面处于允许的变形区域内，需要改变投影面的高度或移动中央子午线。因此，可以采用具有抵偿高程面的任意带高斯正形投影平面直角坐标系作为线路平面坐标系。

3.3 投影高和中央子午线经度的确定

将控制点[ym—Hm]断面线移动，使其处于投影变形要求的区域内，如图2所示。沿[Hm]轴方向移动导致投影面高度发生变化，沿[ym]轴方向移动导致中央子午线发生变化。

在图2中，可直接获取在[Hm]轴、[ym]轴方向上的平移量[-H0]、[-y0]。对直线[y=y0]与设计路线的交点（[x0]，[y0]），进行高斯投影坐标反算获得其大地坐标（[B0]，[L0]），最终获得抵偿高程面的任意带高斯正形投影平面直角坐标系的中央子午线为[L0]，投影高为[H0]。

经计算，某高速公路平面坐标系的中央子午线经度为105°07′17″，投影面高580 m。

3.4 线路平面坐标系下的变形验算

根据线路平面坐标系的投影高及中央子午线，将各控制点的3°带坐标转换为路线平面坐标系下的坐标，将各控制点的大地高换算为相对于新的投影面的高程。然后对线路平面坐标系下的各控制点进行投影变形验算，以及对实测边的边长相对中误差进行计算，以确保各控制点的投影变形和相对中误差满足设计要求。控制点变形验算结果见表2，边长相对中误差见表3。

各控制点处的投影变形量最小值为0.3 mm/km、最大值为23.3 mm/km；边长相对中误差最小值为-1/624 726、最大值为1/40 413。检验结果表明：中央子午线为105°07′17″、投影高为580 m的具有抵偿高程面的任意带高斯正形投影平面直角坐标系能够满足工程需要。

4 结论与建议

具有抵偿高程面的任意带高斯正形投影平面直角坐标系是一种能够高效控制投影变形的坐标系统。通过选择合适的中央子午线和投影高，建立具有抵偿高程面的任意带高斯正形投影平面直角坐标系，可以作为高速公路的平面坐标系。本研究同时提出以下几点建议。

①在控制点埋设时，相邻控制点之间以及控制点与设计路线之间的高差应尽量小，以防止因高差引起的变形量过大。

②在计算控制点处的投影误差时，使用的高度是相对于投影面的大地高度。

③当路线呈东西走向或者路线设计中的标高高差起伏过大，一个平面坐标系无法满足全线的投影变形要求时，可以采用分段建立具有不同抵偿高程面、不同带高斯正形投影平面的直角坐标系作为第二平面坐标系。为了保证两个平面坐标系的良好衔接，需要确保两个平面坐标系有一定的重叠区域，并且重叠区域的投影变形在两个平面坐标系中均要小于或等于25 mm/km，且两个平面直角坐标系的分割区域不能位于重大的构筑物内。

参考文献：

［1］施一民.现代大地控制测量［M］.北京：测绘出版社，2003：156-160.

［2］中华人民共和国交通部.公路勘测规范：JTG Cl0—2007［S］.北京：人民交通出版社，2007.

［3］谢正军，潘国兵，宋礼德.GPS定位技术在山区高速公路平面控制测量中的应用研究［J］.重庆交通大学学报（自然科学版），2008，27（6）：1046-1049.

［4］宋健，尉青梅，王新强.线路工程独立坐标系的建立方法探讨［J］.矿山测量，2018，46（4）：116-119，123.

［5］陶叶青，杨娟，徐长海.建立大型线路工程独立坐标系的方法［J］.测绘科学，2013，38（4）：155-156.

［6］许云燕，孙现申，孙树芳.高速公路测绘中坐标系及投影面的选择［J］.公路工程，2019，44（3）：88-91.

［7］孔祥元，郭际明.控制测量学［M］.武汉：武汉大学出版社，2006.

收稿日期：2023-08-11

作者简介：胡毅（1989—），男，本科，工程师，研究方向：工程测量、激光雷达数据处理。