基于多目标优化模型的扇叶最优分组与排列方案

薛煌铠 宋佳怡 苗育睿

收稿日期：2023-08-04

DOI：10.19850/j.cnki.2096-4706.2024.07.022

摘  要：衡量某种机械单片扇叶结构优劣的指标有“质量”与“转动频率”两种参数，为了合理地装配整个风扇，需要相邻组的扇叶质量差达到最小，同时相邻叶片的频率差达到最大。首先构建一个单目标优化的质量分组模型，其后引入递推型动态规划算法，使得相邻组的扇叶质量差达到最小。同时考虑转动频率的影响，再建立一个多目标优化的质量分组模型，采用动态权重线性加权法，通过对比不同权重下相邻扇叶组的最大质量差和相邻扇叶的最大频率差，发现当A目标和B目标的权重均为0.5时，该模型所给出的方案效果最佳。

关键词：递推型动态规划算法；多目标优化分组模型；动态权重线性加权法

中图分类号：TP391  文献标识码：A  文章编号：2096-4706（2024）07-0100-07

Optimal Grouping and Arrangement Scheme of Fan Blades Based on

Multi-objective Optimization Model

XUE Huangkai， SONG Jiayi， MIAO Yurui

（Beijing Institute of Technology， Beijing  102401， China）

Abstract： The indicators for measuring the quality of a single fan blade structure of a certain machinery include two parameter：“mass”and“rotational frequency”， In order to assemble the entire fan reasonably， it is necessary to minimize the mass difference between adjacent groups of fan blades and maximize the frequency difference between adjacent blades. Firstly， a mass grouping model with single objective optimization is constructed， and then a recursive dynamic planning algorithm is introduced to minimize the mass difference between adjacent groups of fan blades. At the same time， considering the influence of rotational frequency， a mass grouping model with multi-objective optimization is established， and the dynamic weight linear weighting method is used， by comparing the maximum mass difference between adjacent groups of fan blades and maximum frequency difference between adjacent blades under different weights， it is found that when the weights of target A and target B are both 0.5， the scheme provided by the model has the best effect.

Keywords： recursive dynamic planning algorithm; multi-objective optimization grouping model; dynamic weight linear weighting method

0  引  言

某机器的核心部件是由一个中心转轴和多个扇叶构成，转轴和扇叶是分开制造的，然后组装到一起，如图1所示。

图1  某机械扇叶组合安装效果图

在实际加工制造时扇叶的各种参数会产生随机误差，为了使这些扇叶能和转轴配合组装，正常运转，组装时需要在一定条件下进行分组和排序。这里考虑24个扇叶的情况，所有扇叶均匀分布在转轴边上，围成一圈，表1和表2给出了两组扇叶的相关参数值。

扇叶装配时需满足两个目标：

A目标即所有24个扇叶按位置分成6组，每4个连续的扇叶为1组，每组4个扇叶总质量与相邻组4个扇叶总质量的差要小于等于某个尽可能小的定值。

B目标即所有相邻扇叶的频率差要大于等于某一尽可能大的定值。

兼顾目标A和B建立模型，给出使相邻组扇叶质量差尽可能小、相邻扇叶频率差尽可能大、不同参考标准下合理的扇叶分组及排序方式。

1  数据的处理与分析

对于引言中给出的两张表，我们利用Excel分别绘制出叶片的质量分布图和频率分布，如图2所示。

从图2中我们不难看出：两组叶片的质量和频率分布并不是均匀的，而是呈现一个周期性的规律，以6个叶片为单位，相互间具有相近的质量和频率，这也为后续我们对这两项指标的处理提供了重要的信息。

2  单目标优化的质量分组模型

2.1  目标A分析

我们先考虑目标A。从扇叶质量的角度出发，进行分组。共给出了24片扇叶，每4片连续的叶片为1组，总计6组。要求相邻各组的扇叶质量之和的差尽可能小。若用Mci （i ∈ 1，2，…，6）表示这6组分组中第i组的总质量，且考虑到风扇的装配是圆周状，需考虑首尾两组叶片组的质量差，故增加Mc7 = Mc1。由此，我们可以把问题表述为：

min | Mci - Mc（i+1） |                       （1）

当各个组的差均达到最小，考虑最大的那个质量差，可以进一步写成：

min max | Mci - Mc（i+1） |                   （2）

将绝对值改写为平方的形式：

min max（Mci - Mc（i+1））2                  （3）

令函数y = min max（Mci - Mc（i+1））2，由平方的非负性可知y≥0。当且仅当Mci = Mc（i+1）即Mc1 = Mc2 = … = Mc6 =  时（其中 ），函数y达到最小值，且ymin = 0。

于是目标A  每组扇叶质量和越接近6组均值越好

2.2  单目标优化模型建立

基于上述的分析，我们很容易知道这属于一个离散的最优化问题，如何分组才能达到最佳的效果，也就是目标A所要求的质量差最小，各组的质量都接近平均值。于是我们着手构建一个单目标优化[1]的质量分组模型。

2.2.1  确定决策变量

对于本问题而言，决策变量即为分组的方式。我们可以定义一个映射f（f为双射），建立起从叶片编号NO.X到片在分组时的位置Cij的对应关系。而此时的映射关系f即为我们的决策变量：

（4）

2.2.2  确定目标函数

在2.1小节的问题分析中我们知道，我们已经把问题转化成了：每组扇叶质量和越接近6组均值越好，于是我们的目标函数便可参照式（2）写成：

（5）

2.2.3  确定约束条件

在本题中，扇叶的分组方式是有稍加限定的，24个扇叶要被均分成6组，每组有且只有4个扇叶，我们可以利用Cij中i与j的取值来加以限定：

（6）

2.3  模型求解

2.3.1  递推型动态规划算法求解

为了解决最佳质量分组的问题，我们引入动态规划算法[2]，先不考虑全局最优解，也就是不能一步划分成6组。而是将该问题分解成若干个子问题，考虑如果每组只有1个元素，该如何划分；如果每组有2个元素，又该如何划分；这些若干的子问题具有相互的关联性。我们按照这个思路，设计了递推的动态规划算法，图3可以清楚地展示出我们的思路。

为了更直观地展示上述算法的过程，我们绘制了流程示意图，如图4所示。

2.3.2  求解结果分析

利用上述的动态规划算法，我们用Python进行了实现，将最佳分组方案以图表形式进行呈现，最后得到ci的分组策略，如图5所示。

上述得到的ci分组方案，一共有216种组合，且这些组合的相邻组质量差均一致，下面列出表格进行详细说明，如表3所示。

如表3所示，每一组的叶片质量和近乎相等，最大的质量差不超过1 g。可以认为是最大程度符合条件A的最佳分组策略。

我们以同样的思路处理第二组的24个数据，得到的分组策略如图6所示。

第二组叶片的最佳分组方案一共有48种，每一种的各组质量和均相同，我们同样以列表的方式进行了呈现，如表4所示。

如表4所示，第二组数据分组后，每组质量和的差稍大，但最大的质量差不超过2 g。可以认为是最大程度符合条件A的最佳分组策略。

图6  第二组叶片的最佳分组方案图

2.4  模型敏感性分析

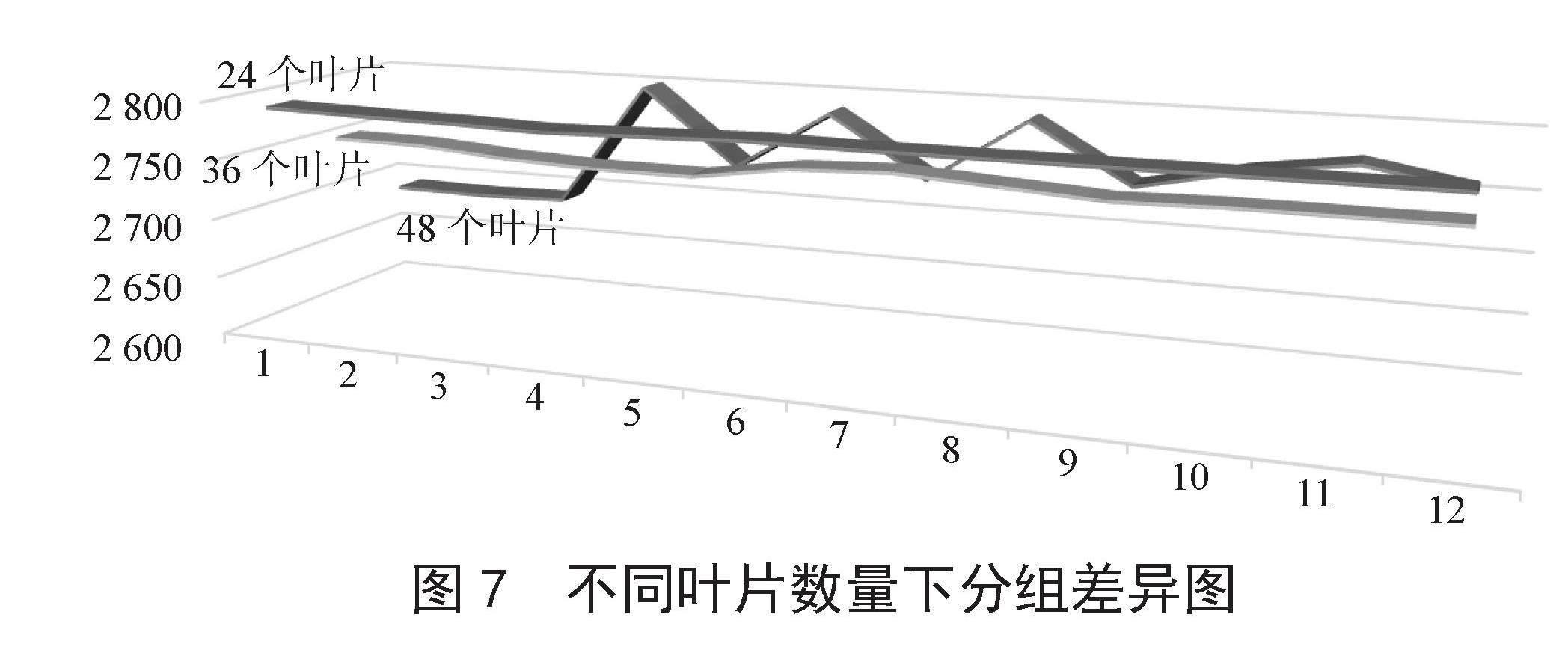
当扇叶数量变为36、48个时，我们的模型是否仍有效？我们将输入的扇叶叶片数量i×j作为自变量，利用题中所给的两组数据，来分别模拟36个和48个叶片的情况，并再次使用我们的动态规划法求解，并比较与在24个叶片时的分组的差距。结果如图7所示。

图7  不同叶片数量下分组差异图

由图7可以明显地看出，随着叶片数量不断增加，组与组之间的质量波动会越来越明显，但总体来看波动均不超过±50 g，故可以认为模型一仍然有效。

3  多目标优化的质量分组模型

3.1  双目标分析

同时兼顾目标A和目标B，在上一节中我们已经知道，目标A的目标就是让各组的质量差?Mci尽量达到最小，而目标B则是要求在此基础上让每两个相邻叶片的频率差尽可能大，即? fij尽可能大（表示第i组的第j个扇叶与下一扇叶频率差值）。这属于一个典型的多目标离散分组问题，下面我们建立多目标优化的分组模型[3]来解决问题。

3.2  多目标优化模型建立

3.2.1  确定决策变量

这次我们将24组叶片的排列顺序直接当成一个解，用ck表示24个叶片中的第k（k≤24）个叶片，此时我们用g来表示当前的一个顺序解，g = c1c2…c24c25（c25 = c1）。要说明的是g代表一种排列方案，所有可行的解g构成解空间（决策空间）G = g。所以我们的决策变量就是排序方案g。

3.2.2  确定目标函数

根据上一节我们可以由式子（5）导出A条件对应的目标函数：

（7）

式（7）表示了组与组之间的质量差最小。接下来同样给出条件B对应的目标函数：

（8）

这个函数表示了所有相邻叶片的频率差最大化。

3.2.3  确定约束条件

本问的约束条件同上一问，但由于重新规定了排序，因此在数值上有一些小改动：

（9）

3.3  模型求解

3.3.1  动态权重线性加权法

在上一节中，我们已经知道现在需要求解的是一个多目标的离散的组合优化问题，可以把时（7）至式（9）的所有方程组列出如下：

一般来说，对于这种多目标规划问题的绝对最优解是不常见的，对绝大多数的多目标决策的实际问题，我们一般偏好的方案是有效解或非劣解，也称为Pareto最优解[4]。

首先，我们先将2个最大和最小的不同方向的函数转化成方向一致的求最小值问题：

（10）

之后考虑到A条件与B条件的重要程度可以不同，于是采用动态权重线性加权法[5]，给予每项不同的权系数wj （0≤wj≤1，j = 1，2），从而充分体现出每个目标的不同重要程度对结果的影响：

（11）

3.3.2  交替迭代的模拟退火算法

我们已经对目标函数做了一定的处理，接下来我们需要引入模拟退火算法。示意图如图8所示。

图8  模拟退火算法示意图

模拟退火算法是一种通用的随机搜索算法，其基本的思想来源于固体的退火过程，是一种基于概率的算法：将固体加温至充分高，再让其徐徐冷却。加温时，固体内部粒子随温度升高变为无序状态，内能增大；而徐徐冷却时粒子渐渐趋于有序。在每个温度都达到平衡态后在常温下达到基态，内能减为最小，以优化问题的求解与物理过程退火的相似性为基础，适当地控制温度的下降过程，实现模拟退火从而达到全局优化的目的[6]。

本文通过PDMOSA求解，PDMOSA是Suman[7]在2004年提出的多目标模拟退火算法。该算法通过基于Pareto支配的适应度计算劣解的接受概率。该适应度被定义为当前Pareto解集中支配该解的数量加1。PDMOSA比其他多目标模拟退火算法效率更高。此外，作为一种单轨迹搜索算法，PDMOSA在求解VRP问题上有优势[8，9]。

模拟退火算法被用于解决各种组合优化问题，下面是本模型使用模拟退火算法求解的基本过程：

1）定义状态：将每个扇叶的排序g = c1c2…cu…cv…c24作为问题的一个状态，其中每个状态表示一种扇叶的排序方式。

2）初始化当前状态为一个随机的初始分组方式。

3）设置初始温度T0和终止温度Tend，以及温度下降的速率e = 0.99（退火率）。

4）迭代执行以下步骤直到达到终止条件（例如达到终止温度或达到最大迭代次数）：

步骤1：产生当前状态的邻域状态，可以通过交换两个不同编号的扇叶（如cu与cv）排序得到邻域状态g' = c1c2…cv…cu…c24。

步骤2：计算当前状态和邻域状态之间的目标函数值差异? fij = min f （g） - min f （g'）（即相邻组的目标函数差值）。

步骤3：如果目标函数值差异为负（即邻域状态更优），则接受邻域状态作为新的当前状态。

步骤4：如果目标函数值差异为正（即邻域状态较差），则以一定概率接受邻域状态。接受劣解的概率由Metropolis准则[10]来确定。

步骤5：更新温度，降低温度值。

5）返回最终收敛到的当前状态作为最优分组方式及相邻关系。

在每次迭代中，通过接受劣解的策略，退火算法能够逐步减小温度，使算法逐渐趋向于全局最优解。最终，退火算法将收敛到一种扇叶分组方式，使得相邻组之间的总质量差值最小。

用图9所示的流程图可以更直观地描述模拟退火算法。

3.4  最终结果分析

我们利用Python程序运行模拟退火算法，求出了在不同权重下的Pareto最优解，下面我们将分情况展示：

1）情况一：Wm = 0.5、Wf = 0.5时，最优分组编号排序如表5所示。

在权重配比都为0.5时，我们的结果很好地符合了组与组之间质量差小、片与片之间频率差大的规律。从图10中也可以直观地看出，两组数据均满足条件。

2）情况二：Wm = 0.7、Wf = 0.3时，最优分组编号排序如表6所示。

当我们把质量差的权重调到0.7，频率差的权重为0.3时，从图11可以看到在最大质量差基本没有改变的情况下，频率的波动有减小的趋势，最小频率差也在减小。

3）Wm = 0.3、Wf = 0.7时，最优分组编号排序如表7所示。

当我们把质量差的权重调到0.3，频率差的权重为0.7时，可以从图12中看出质量差的波动稍有变大，而频率差则基本无变化。

综上所述，我们发现当A条件和B条件的权重均为0.5时，该模型所给出的方案是效果最佳的，既满足组与组质量差最小，又满足片与片频率差最大化。其余两种权重下，虽然与第一种方式有差异，但差异较小，也可作为不同装配方案的参考。

4  结  论

本文针对扇叶装配的常见要求，以24个叶片规格的扇叶为基础，依次分析质量与转动频率两种参数对装配方案产生的影响和最佳分组策略。

首先考虑单目标质量指标，即使得相邻组的扇叶质量差达到最小，构建单目标优化的质量分组模型，其后引入递推型动态规划算法辅助最优分组。表1扇叶经处理得到216种相邻组质量差均一致的组合，每一组最大的质量差不超过1 g；表2组叶片的最佳分组方案一共有48种，最大的质量差不超过2 g。此外，对于不同叶片数量的情况进行了模型灵敏度分析，应用模型和算法，带入不同数量（36、48个）的叶片质量和频率，发现随着叶片数量不断增加，组与组之间的质量波动会越来越明显，但总体来看波动均不超过±50 g，可以得出该分组策略对于不同数量扇叶基本适用。

在此基础上同时考虑“转动频率”的影响，即满足相邻个的叶片的频率差达到最大化。建立多目标优化的质量分组模型，采用动态权重线性加权法，给予质量与转动频率两种参数不同的权系数，从而充分体现出每个目标的不同重要程度对结果的影响。在模型的基础上，使用交替迭代的模拟退火算法得到最优解。通过对比不同权重下，相邻扇叶组的最大质量差和相邻扇叶的最大频率差，发现当A条件和B条件的权重均为0.5时，该模型所给出的方案是效果最佳的。

综上，本文通过合理构建数学模型与计算机辅助求解的方法，创新性提出合理的加工装配方案，该机械涡扇的技术人员可依据上述方案，为该类型的扇叶提供更准确的理论安装指导。

参考文献：

[1] 王依凡，叶宏达，邱子杰，等.基于单目标优化的众包任务定价模型 [J].实验科学与技术，2018，16（5）：1-5+29.

[2] 王茂萍，潘大志.求解集值折扣{0-1}背包问题的改进动态规划算法 [J].计算机应用与软件，2022，39（9）：274-277.

[3] 吴瑞霞.模糊多目标优化的分类与特征选择方法和应用 [D].烟台：鲁东大学，2021.

[4] 刘仁云，张美娜，姚亦飞，等.一种新的全局排序高维多目标优化算法 [J].吉林大学学报：理学版，2022，60（3）：664-670.

[5] 王一华.中国大陆图书情报专业期刊的综合评价——基于熵权法、主成分分析法和简单线性加权法的比较研究 [J].情报科学，2011，29（6）：943-947.

[6] 贾天理，喻若舟，王思凯，等.函数最值计算的模拟退火算法设计与应用研究 [J].黑龙江科学，2022，13（1）：149-151.

[7] SUMAN B.Study of simulated annealing based algorithms for multiobjective optimization of a constrained problem [J].Computers & Chemical Engineering，2004，28（9）：1849-1871.

[8] WANG J H，ZHOU Y，WANG Y，et al. Multiobjective Vehicle Routing Problems With Simultaneous Delivery and Pickup and Time Windows： Formulation， Instances， and Algorithms [J].IEEE Transactions on Cybernetics，2016，46（3）：582-594.

[9] 毕志升.基于多目标模拟退火的团队定向问题 [J].自动化与仪器仪表，2017（5）：41-44+47.

[10] 邓绍强，郭宗建，李芳，等.基于Metropolis准则的自适应模拟退火粒子群优化 [J].软件导刊，2022，21（6）：85-91.

作者简介：薛煌铠（2003—），男，汉族，福建福州人，本科在读，研究方向：数学建模与应用；宋佳怡（2004—），女，汉族，山东青岛人，本科在读，研究方向：数学建模与应用；苗育睿（2004—），女，汉族，北京人，本科在读，研究方向：数学建模与应用。