基于响应面法的高性能复合砂浆参数优化研究

李英飒 冯亚楠

摘 要：【目的】研究高性能复合砂浆配合比设计参数。【方法】采用响应面 Box-behnken 试验设计法开展了硅灰掺量、水胶比和石英粉与石英砂比值等3个自变量对高性能复合砂浆抗压强度的影响研究，经响应面预测、验证获得最佳配合比参数。【结果】高性能复合砂浆的抗压强度随着水胶比的增大而减小；随着硅灰掺量的增加，略有增加，但增幅较小；随着石英粉/石英砂增加或减小影响程度并不明显。【结论】所建模型在试验范围内能较准确地预测结果，响应面法用于高性能复合砂浆配合比参数优化具有准确性与科学性。

关键词：响应面法；高性能复合砂浆；配合比设计；抗压强度

中图分类号：TU528.31     文献标志码：A    文章编号：1003-5168（2024）07-0088-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.07.017

Parameter Optimization of High Performance Composite Mortar Based on Response Surface Methodology

LI Yingsa FENG Yanan

（China Railway Communications Investment Group China Railway Zhongnan Investment Development Co.， Ltd.， Changsha 410100，China）

Abstract：[Purposes] This paper aims to study the design parameters of the mix ratio of high-performance composite mortar. [Methods] The Box-behnken test design method was used to study the effects of three independent variables on the compressive strength of high-performance composite mortar， namely， the content of silica fume， the water-binder ratio and the ratio of quartz powder to quartz sand. The optimal mix ratio parameters were obtained by the response surface prediction and verification. [Findings] The compressive strength of high-performance composite mortar decreased with the increase of water-binder ratio. With the increase of silica fume content， it increases slightly， but the increase is small. With the increase or decrease of quartz powder/quartz sand， the degree of effect is not obvious. [Conclusions] The established model can predict the results more accurately in the test range， and the response surface method is accurate and scientific in the optimization of the mix ratio parameters of high-performance composite mortar.

Keywords： response surface methodology; high performance composite mortar; mix proportion design; compressive strength

0 引言

隨着经济快速发展，普通混凝土由于耐久性差、自重大、脆性高、强度低等缺点，已不能普遍满足所有需求。通过不断的研究，国内外出现了各类性能优异的混凝土［1］。高性能复合砂浆因其具有较高的强度、韧性等优点，广泛应用于各重大工程项目［2］。对比普通混凝土，高性能复合砂浆由于其组分复杂，在配合比优化中需要考虑更多的因素。

响应面法（Response Surface Methodology，RSM）运用回归方程对合理的试验设计得到的相关数据进行拟合，得到设计变量与目标函数之间的近似函数关系，是处理优化问题的常用方法之一。响应面法最初多应用于生物食品等领域，解决食品工艺配方问题，随后在建筑材料及混凝土等领域也得到了广泛应用。赵士豪等［3］通过对抗压强度进行响应面分析，对超高性能混凝土配合比进行优化设计；吴永根等［4］利用响应面法以高性能合成纤维道面混凝土为研究对象，探究混凝土冻融及冻蚀劣化分析；陈露一等［5］通过响应面法获得合适的早强剂掺量，制备出性能良好的超早强混凝土。吕官记等［6］利用响应面法对三元聚合物砂浆配合比进行优化。目前，基于响应面法研究高性能复合砂浆配合比优化的研究相对较少，基于响应面法分析水胶比、硅灰掺量及石英砂与石英粉在高性能复合砂浆的研究更是稀缺。本研究运用响应面法，探究双因素之间对高性能复合砂浆力学性能的影响，从而形成一种高性能复合砂浆配合比参数优化方法，以推动砂浆的实际工程应用。

1 材料与方法

1.1 原材料

本研究采用郑州天瑞水泥有限公司生产的42.5普通硅酸盐水泥，初凝时间146 min，28 d抗压强度为50.2 MPa。硅灰来自郑州筑邦建材有限公司，表观密度为2.232 g/cm3。粉煤灰由经纬建材有限公司生产，密度为2.4 g/cm3。采用石英砂20～40 目，密度为2.654 g/cm3。石英粉采用325目，密度为 2.626 g/cm3。采用减水率大于30%聚羧酸高效减水剂。PE纤维由湖南中泰特种装备有限责任公司生产，长度为12 mm。

1.2 试验方法

高性能复合砂浆的抗压强度根据《水泥胶砂强度检验方法（ISO法）》（GB/T 17671—2021）进行测试。

1.3 试验设计

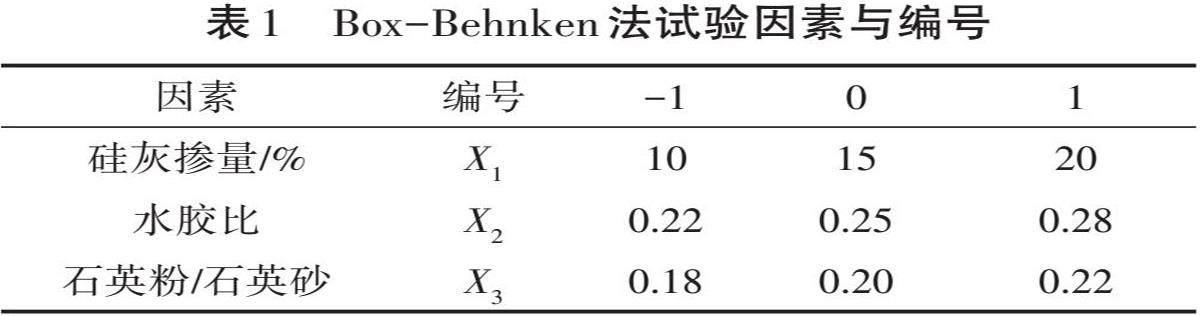
在单因素试验的基础上，保持胶砂比1，长度12 mm的PE纤维以体积2%掺量不变，减水剂掺量占胶凝材料质量的2%不变，以硅灰掺量、水胶比和石英粉/石英砂的比值为自变量，分别以X1、X2、X3表示。以28 d的抗压强度（MPa）为响应值，以Y表示，各因素选取三水平，以-1、0、1编码，将试验结果进行回归拟合，其中，硅灰掺量为占胶凝材料质量的百分数，水胶比是水与胶凝材料质量的比值。Box-Behnken法试验因素与编号见表1。

2 试验结果

Box-Behnken 设计方法进行试验，共计17组，试验结果如表2 所示。

对表2中抗压强度数据进行回归拟合分析，采用Design-Expert 8.0.6软件对结果进行拟合分析，采用二阶多项式模型建立抗压强度Y与X1、X2、X3的模型，多项式模型表示如式（1）。

Y=76.88+1.14X1-13.17X2+1.59X3-1.27X1X2+3.00X1X3-

0.82X2X3+1.13X12-2.49X22+2.29X32 （1）

对上述回归方程进行方差分析，抗压强度回归方程方差分析见表3，模型采用F检验对模型进行判定。由表3可知，抗压强度的二次多项式回归方程的所有P值<0.000 1，可认为此模型极为显著；失拟项分别为0.14 38大于0.05，表明该试验数据与模型不相关的情况不显著，说明拟合效果较好，可以很好地描述响应和因素之间的关系。经方差分析，Y回归方程一次项X2的P＜0.01，表明X2对结果影响极显著， 一次项X1的P＜0.1，表明X1对结果影响较显著。Y的一次项X3对结果影响较显著（P＜0.1）。Y的回归方程交互项X1X2、X2X3和X1X3对结果影响显著（P＜0.05），二次项X12、X22、X32对结果影响极显著（P＜0.01）。

2.1 模型可行性检验

R2和校正系数Adj-R2的接近程度可以用来验证回归方程的拟合程度，R2与R2校正系数越接近于1，说明模型可靠程度越好，预测精准度越高。本模型中 Y模型方程R2校正系数分别为0.973 8，R2预测系数分别为0.864 8，R2校正系数与R2预测系数的差值小于0.2，说明该模型能够解释其响应过程；信噪比大于4，说明实验结果可靠，该值越大，表明干扰因素的影响越小。变异系数均小于10，说明试验的可信度和精确度高，可以用二阶模型的回归方程对试验结果进行模拟分析［7］。Y的残差正态图接近一条直线，说明回归模型拟合得越好。模型的实际值与预测值数据点基本处于一条直线上，从而证明了数据集是正态分布的。

2.2 两因素交互作用分析

为更加深入的研究硅灰掺量、水胶比和石英粉/石英砂对抗压强度的影响，通过固定其中一个因素的值，研究另外两种因素的交互作用对响应值的影响。建立了试验因素交互作用的3D响应面曲线和等高线。

2.2.1 硅灰掺量、水胶比对抗压强度的交互影响。硅灰掺量与水胶比对抗压强度的3D响应面曲线和等高线如图1所示。由图1可知，随着从水胶比从0.22～0.28的變化过程中，随着水胶比的增加，抗压强度逐渐减小，从三维响应曲面的走势可以对比出水胶比和硅灰掺量两因素对抗压强度的影响显著程度，抗压强度随水胶比因素的变化在曲面上表现得更为陡峭，说明影响更大。硅灰掺量为20%时，抗压强度随水胶比的增大而减小，抗压强度在水胶比0.22，硅灰掺量20%时达到最大。

2.2.2 硅灰掺量、石英粉/石英砂对抗压强度的交互影响。硅灰掺量、石英粉/石英砂对抗压强度的3D响应面曲线和等高线如图2所示。由图2可知，反当硅灰掺量一定时，随着从石英粉/石英砂从0.18～0.22的变化过程中，抗压强度的走势是先减少后增加，且在硅灰掺量20%，石英粉/石英砂为0.22时，抗压强度最大。响应面呈现凹型，对比两个因素对响应值的影响可以看出，硅灰掺量与石英粉/石英砂的影响并非十分明显。

2.2.3 水胶比、石英粉/石英砂对抗压强度的交互影响。水胶比、石英粉/石英砂对抗压强度的3D响应面曲线和等高线如图3所示。由图3可知，水胶比与石英粉/石英砂对抗压强度的影响随着水胶比的增加而下降，但从等高线可以看出，随着水胶比的增加，随着试块龄期的增长，抗压强度下降也越来越不明，体现在3D响应曲面的陡峭程度变缓及等高线中的等高线分布越来少。从三维响应曲面的走势可以对比出水胶比因素对抗压强度的影响显著，当因素X3固定时，抗压强度随因素X2的变化在曲面上表现得更为陡峭，因此水胶比因素对抗压强度的影响显著程度要大于石英粉/石英砂。

2.3 响应面最优化分析结果预测与验证

利用Design-Expert8.0.6的Numerical功能对表2中的数据进行配合比优化。优化时，在试验因素水平范围内选择抗压强度最大值作为优化目标，求解模型的最优化值。软件模拟分析得出的最优化参数为：硅灰掺量20%、水胶比0.22、石英粉/石英砂为0.22，以最优参数作为试验条件。为验证模型预测结果的可靠性和准确性，按照模型优化的参数进行3组平行试验，取平均值作为验证结果，抗压强度的相对偏差分别为1.9%。验证结果与预测结果相差不大，证明响应面模型与分析准确与可靠，可以真实地反映硅灰掺量、水胶比、石英砂与石英粉的比值对高性能复合砂浆的力学性能的影响。

3 结论

本研究采用响应面法研究了硅灰掺量、水胶比、石英粉/石英砂对高性能复合砂浆力学性能的影响以及各因素之间的交互作用，结论如下。

①采用响应面模型中的Box-Behnken试验建立进行以硅灰掺量、水胶比、石英粉/石英砂为影响因素，抗压强度为响应值的回归模型，经过分析及检验，所建模型在允许的范围内可以较为准确地预测结果，预测与实际值相对误差较小，证明了模型的可靠、科学与准确性。

②在影响抗压强度的三个试验因素中，抗压强度随着水胶比的增大而减小；随着硅灰掺量的增加，略有增加，但增幅较小；随着石英粉/石英砂增加或减小影响程度并不明显。对抗压强度影响强弱顺序依次为：水胶比＞硅灰掺量＞石英粉/石英砂。

③将抗压强度的最大值作为目标的优化目标值，得出高性能复合砂浆的目标优化参数为：硅灰掺量20%、水胶比0.22、石英粉/石英砂为0.22。

参考文献：

［1］雒敏.超高性能混凝土构件力学性能及承载力的试验与理论研究［D］.兰州：兰州交通大学，2021.

［2］邓明科，马福栋，张阳玺，等.活性粉末混凝土抗压强度试验研究［J］.硅酸盐通报，2017，36（8）：2731-2736.

［3］赵士豪，林喜华，车玉君，等.基于DE响应面分析的C100超高性能混凝土配合比优化设计［J］.混凝土与水泥制品，2018（8）：24-28.

［4］吳永根，吴豪祥，蔡良才，等.基于响应面法的高性能合成纤维道面混凝土冻融及冻蚀劣化分析［J］.科学技术与工程，2020，20（25）：10428-10432.

［5］陈露一，张志豪，黄有强，等.基于响应面法的超早强混凝土优化设计［J］.世界桥梁，2018，46（4）：17-21.

［6］吕官记，季韬.基于响应面法的三元聚合物砂浆力学性能［J］.建筑材料学报，2021，24（5）：970-976.

［7］石振武，解飞.基于响应面分析法的钢纤维混凝土耐磨性试验研究［J］.公路交通科技，2015，32（7）：23-27.

收稿日期：2023-11-17

作者简介：李英飒（1979—），女，本科，高级工程师，研究方向：水泥基复合材料。