考虑水盆效应隧道道床上浮力学特征及计算分析
熊成宇 田茂霖 朱荣辉 刘宁

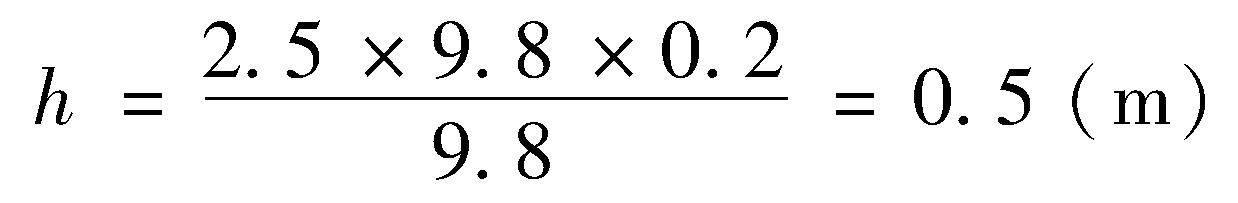
摘 要:围绕富水隧道道床上浮底鼓工程问题,本文探索将水盆效应引入隧道无砟道床上浮底鼓病害的研究中。首先,基于应变能和能量理论,结合结构层间接触力学条件,开展隧道道床应力和变形量推导,以验证水盆效应与道床上浮关联的合理性。其次,构建道床变形挠曲线方程和应力和最大变形量公式,得到基底0.5 m水头高度可以引起粘结失效道床上浮底鼓,并通过设定上浮临界水头值划分上浮三阶段:1) 初期入渗汇水阶段;2) 局部积水阶段;3) 水盆上浮阶段。最后,建立不同排水状态下道床横向及纵向上浮量计算公式,形成基底水流量差、压力速率分别与上浮速率及上浮量的关系曲线,形成隧道道床上浮的最小水头高度的计算方法,以助力道床上浮控制的研究和治理措施的改进。
关键词:富水隧道;道床上浮;水盆效应;力学特征
中图分类号:TU43
文献标志码:A
我国各地的许多隧道均存在渗漏水情况。隧道渗漏水会导致道床混凝土劣化[1-2]、道床上浮[3],道床上浮是隧道工程中较为常见的一种病害[4-5],道床上浮会严重危害结构稳定和车辆安全及平顺性。国外已经有许多因膨胀围岩引起的仰拱底鼓病害[6],通过理论公式推导可以揭示道床脱空上浮的本质原理[7-8],然而目前研究主要集中在道仰拱底鼓引起的道床上浮及隧道仰拱底鼓量的预测。仰拱底鼓的原因有许多种,ANAGNOSTOU[9]采用弹塑性理论模拟膨胀围岩,分析了膨胀围岩区隧道仰拱变形及其底鼓机制。BUTSCHER等[10]分别从微观及宏观角度研究了隧道开挖导致周边水文条件变化,地下水流入隧道周边膨胀性围岩导致仰拱隆起。钟祖良、刘新荣等[11]采用連续介质力学原理,推导了软岩隧道仰拱底鼓量的理论公式,可为类似隧道底鼓量的预测提供依据。师亚龙、陈礼伟等[12]运用弹塑性力学原理分别推导了各种因素引起的底鼓量,并得出了底鼓量预测的组合公式。WITTKE GATTERMANN[13]采用弹塑性力学原理,考虑材料各向异性,并引入时间变量,建立了膨胀性围岩本构模型。秦巴列维奇[14]基于松散土体压模试验分析,采用土体极限平衡理论,开展了底鼓巷道土压力及其机理的计算分析。
国内外的研究主要集中在仰拱底鼓引起道床上浮,尚未见有水盆效应引起道床上浮相关的研究。上述理论研究均针对的是隧道底鼓现象,且均为外部因素如围岩压力、围岩膨胀性等方面引起隧道底鼓。然而,结合隧道工程上浮底鼓问题研究,道床板粘接强度完整,需要较高临界水头引起道床与仰拱填充之间的上浮底鼓。但实际工程上浮水头高度较小,有必要开展隧道道床上浮力学问题的计算分析的研究。
1 水盆效应及计算基本假定
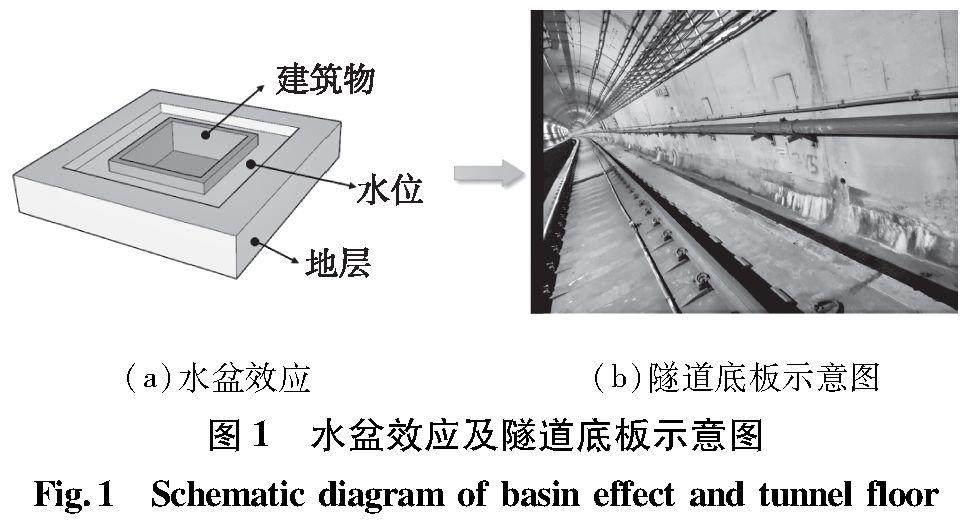
建筑工程中首先提出的一个“水盆效应”名词,根据李卫平[15]的研究,水盆效应是指基坑回填土的分层夯实不达标,使得地表水、地下水以及施工用水等四周水汇入坑内和地下室底板下面。在基坑四周为不透水土层和坑内水滞留情况下,当底板滞留水的上浮浮力大于地下室抗浮力时,则地下室发生上浮现象。水盆效应示意图见图1(a)。
在水盆效应及二衬背后水压力共同作用下,无砟道床可以在较小的水头高度下发生上浮,本文创新将 “水盆效应”引入隧道道床上浮分析中,如图2所示。
本文依托贵阳市轨道交通二号线无砟道床发生上浮的案例,通过查阅相关资料,从理论分析及数值模拟分析等方面,深入研究水压力引起的无砟道床上浮现象(如图1(b)所示)。因此,将水盆效应引入隧道无砟道床上浮病害的研究中,运用能量理论对无砟道床的应力和变形量理论解进行推导,对水盆效应如何影响道床上浮进行探究,助力道床上浮机理的研究以及相应治理措施的改进。本文采用能量法计算道床上浮量。能量法是求解任何弹性结构的基本方法。在外力作用下,利用功能原理求解结构指定点的位移称为能量法,它也是有限单元法的基础。能量法有如下几个特点:① 求解简便、迅速;② 不受材料和形状的限制;③ 适用于各种弹性结构、非弹性结构、塑性结构等;④ 可用来求解各种超静定问题。基于上述理论方法,道床上浮求解的基本假设如下:
1)连续性假设
隧道道床混凝土是连续的,不考虑内部孔隙影响,可以用一个连续函数表示道床混凝土的应力、应变、位移等相关力学参数。
2)均匀性假设
道床混凝土是均匀的,即混凝土内部任取一微小单元,其力学性能均与道床整体的力学性能相同。
3)各向同性假设
道床混凝土是各向同性的,即任何方向上具有相同的力学性能。
4)小变形假设
道床混凝土的变形量远小于道床的几何尺寸。
2 考虑水盆效应作用下道床应力和变形量推导
2.1 隧道道床上浮三阶段划分
1)应变能和功能原理
应变能:由于外部荷载引起结构变形而内部储存的能量称为应变能Vε。
功能原理:在弹性体中,外力所做的功全部转化为弹性体内的应变能,可以认为在弹性体变形过程中,弹性体内积蓄的应变能等于外力所做的功,即
Vε=W(1)
根据功能原理可以计算出弹性体发生基本变形的应变能。基于叠加原理,结构组合变形(轴向拉压+圆轴扭转+平面弯曲)应变能表示为
卡氏定理的主要内容是:线弹性范围内,结构应变能对某个力的偏导数,等于结构沿此力方向上的位移(转角),即
因此,对于3种基本变形的位移,有
轴向拉压:
圆轴扭转:
平面弯曲:
组合变形:
2)临界水头公式推导
沿纵向取1 m道床板进行受力分析,此时道床相当于两端固定的梁,设道床宽度为l,道床厚度为d,如图3所示。
其受力简图如图4所示。
道床板受到自重G、道床与仰拱之间粘接力fz以及浮力f浮影响,当f浮大于道床板自重G与粘接力fz之和时,道床板即会发生上浮(上挠)。上浮条件为
f浮≥G+fz(8)
γh≥ρgd+σ(9)
式中:道床自重G=ρgV=ρgdl,粘接力fz=σs=σl,浮力f浮=γhs=γhl。
取道床板厚d=200 mm;混凝土密度ρ=2 500 kg/m3;重力加速度g=9.8 m/s2,水的重度γw=9.8 kN/m3。粘接强度σ=0,则
如果道床与仰拱填充间粘接强度完全失效,则道床仅在0.5 m水头高度下即可发生上浮。
将20 cm板厚临界水头高度h和粘接强度σ的关系绘制成函数图像如图5。
从图6中可以看出道床板厚对临界水头的影响远远小于道床与仰拱填充之间的粘接强度。若粘接强度失效,则在很小的水头高度对应的水压力作用下,道床即可发生上浮。
根据上述隧道底部结构上浮与层间粘接强度的发生发展规律分析,隧道底部结构上浮过程可以分为三个阶段(见图7): 1) 初次上浮阶段,即入渗汇水;2) 第二次上浮阶段,即基底积水阶段;3) 第三次上浮阶段,即脱离上浮阶段。由隧道基底水贯通入仰拱内,填充到结构层底部引起的结构上浮的阶段称为隧道初次上浮;由于基底水进入仰拱内后形成滞留水引起的结构局部变形称为第二次上浮底鼓阶段;隧道第三次上浮是由于结构层间粘结失效,形成具有水盆效应的滞留水层。
2.2 道床变形挠曲线方程推导
由图4的受力分析图可知:将道床简化为梁单元,得到道床发生变形后的轴线,称为道床挠曲线。
挠曲线方程为
ω=f(x)(10)
在小变形情况下的道床转角和挠度有如下关系:
梁在只受到弯矩作用下的曲率与弯矩关系为
由于剪力对道床变形影响很小,可以忽略不计,而曲率和弯矩均为x的函数,即
在数学上曲率与方程有如下关系:
在小变形情况下ω=l;1+ω′2≈1,此时
因在土木工程领域一般以挠度向下为正,所以有
EIω″≈-M(x)(16)
将上式积一次分可得转角方程
再次积分可得挠曲线方程
结合两端固定梁边界条件:x=0和x=l时θ=0;ω=0,荷载为均布荷载q,带入式(18)可得挠曲线方程
2.3 应力和最大变形量公式推导
采用能量法计算道床上浮量。由于道床为对称结构受到对称荷载的作用,可取一半结构进行分析,右端简化为定向支撑,解除右侧约束,代之以支座反力,并将浮力、粘结力、自重转化为一个线荷载q,如图8所示。
设右端为原点,则弯矩函数为
M(x)对MB求偏导,得
根据卡氏定理,结合边界条件,θB=0,可得
为求得最大位移,在右端虚加集中力Ff,如图9所示。
則弯矩函数变为
M(x)对Ff求偏导,得
根据卡式定理,得
3 考虑不同排水阶段下道床上浮量的推导
根据高新强[16]推导的深埋隧道限排情况下衬砌背后水压力公式,若隧道为浅埋隧道且为全包型防水,衬砌完全不透水,衬砌背后不设排水系统,则衬砌背后的水压力即为静水压力,不进行折减。衬砌背后水压力为
3.1 不排水情况讨论
假设渗入到道床与仰拱填充面间的水压力与衬砌外水压力相同,若隧道为全封堵情况或排水管完全堵塞,则相当于渗透系数K1→0,根据式(28)可得水压力为
即水压力与初始水头对应的水压力相等。
1)横向脱空情况
2)纵向脱空情况
3.2 堵水限排情况讨论
假设渗入到道床与仰拱填充面间的水压力与衬砌外水压力相同,若隧道为堵水限排情况,排水管部分堵塞,则相当于渗透系数K1减小,根据式(28)可知水压力会适当增大。设增大后的水压力为ξ1γwh。
1)横向脱空情况
2)纵向脱空情况
3.3 以排为主情况讨论
假设渗入到道床与仰拱填充面间的水压力与衬砌外水压力相同,若隧道为以排为主的情况,排水管效率增大,则相当于渗透系数K1增大。
根据式(28)可知水压力会大大减小。设减小后的水压力为ξ2γwh。
1)横向脱空情况
2)纵向脱空情况
当ξ2→0时,ξ2γwh→0,由此可知在道床上增设排水孔可大大减小道床与仰拱填充之间的水压力。
3.4 不连通情况讨论
假设地下水进入道床与仰拱填充之间后无法排出,由于水的不可压缩性,地下水会将道床顶起。显然道床的上浮量与渗入道床与仰拱填充之间的水量大小有一定的关系,下面将以横向脱空为例推导渗水量与道床上浮量之间的关系(见图10)。
1)横向脱空情况
已知道床变形后的挠曲线方程为式(19),在数学上,积分表示函数与x轴围成的面积,如图11所示,将式(19)积分1次可得道床上浮后的横截面积增加量A:
因横向脱空情况下l=B,经计算可得
此时可得道床上浮后单位长度脱空体积增加量V:
V=A×1=A(38)
因为道床脱空体积完全被水充满,所以可得单位长度渗水量Vw:
又因为道床上浮量最大值表达式为
因此,可以得出单位长度渗水量与横向脱空上浮量最大值之间的关系:
若流入与流出仰拱填充面的水量不相等,有以下几种情况:
对式(41)进行t(时间)求导,可得
假设过水断面面积的流入与流出相等,
将式(41)带入式(44),得
根据公式可得到如下曲线,如图12、13所示。上浮速率与道床与仰拱填充面水压力变化速率成正比,上浮速率会随着流量差的增大而增大,并且在流量差越大的情况下,上浮量的变化也越大,这种变化一开始是缓慢的,随着流量差的变化而逐渐变快。
2)纵向脱空情况
对于纵向脱空情况,设总渗水量为V′w :
式中:l为纵向脱空长度。
因此可以得出總渗水量与纵向脱空上浮量最大值之间的关系:
若流入与流出仰拱填充面的水量不相等,则有
根据公式可得到如下曲线,如图14、15所示。上浮速率与道床与仰拱填充面水压力变化速率成正比,上浮速率会随着流量差的增大而增大,并且在流量差越大的情况下,上浮量的变化也越大,这种变化一开始是缓慢的,随着流量差的变化而逐渐变快。变化倾向与横向脱空情况一致,但是因为纵向脱空长度的关系,在数值上发生了明显的变化。
4 结论
从隧道道床上浮的典型背景工程问题出发,将隧底基岩等效为均匀渗流体系,引入应变能和功能原理,结合结构层面接触力学条件,开展考虑水盆效应隧道道床上浮力学特征及计算分析研究。
1)建立板厚临界水头高度和粘接强度的关系函数,形成隧道道床上浮临界水头计算公式,得到在0.5 m水头高度可以引起粘结失效道床的上浮,并建立了道床变形挠曲线方程和应力和最大变形量公式。
2)根据隧道基底不同的排水状态,将承受对称荷载的道床进行力学简化分析可知,在粘接强度失效条件下,道床上浮仅需要较小水头高度。并建立了流量差与上浮速率、上浮量关系,和压力速率与上浮速率、上浮量关系曲线。随着道床与仰拱填充面水压力的增高,上浮量逐渐增大。
3)形成了道床上浮三阶段的底鼓演化过程。考虑粘结强度,通过理论计算引起道床上浮的最小水头高度,并结合相关力学知识对水盆效应引起道床横向及纵向上浮量进行估算,验证了水盆效应引入道床上浮研究中的合理性。考虑水盆效应推导隧道道床上浮底鼓公式,可以较好地表征地下工程上浮问题。
参考文献:
[1]许敏娟, 陈莹莹, 刘浩. 基于全景图像的隧道渗漏水病害识别方法[J]. 铁道学报, 2023, 45(8): 184-192.
[2] NIEDOSTATKIEWICZ M. Degradation of the concrete railway track bed located in the vicinity of the loading wharf[J]. Polish Maritime Research, 2018, 25(4): 149-153.
[3] 郭志州, 栾忠杰. 香炉山隧道漏水原因分析及改造设计[J]. 北方交通, 2015(7): 97-99.
[4] 华科. 成贵铁路隧道渗漏水缺陷整治技术[J]. 高速铁路技术, 2021, 12(4): 55-59.
[5] 何昌国, 黄棋, 赵万强. 贵广铁路岩溶隧道水害原因分析及整治措施[J]. 高速铁路技术, 2018(增刊1): 67-73.
[6] CHARPENTIE D, MOSSER-RUCK R, CATHEL M. Oxidation of mudstone in a tunnel (Tournemire, France): consequences for the mineralogy and crystal chemistry of clay minerals[J]. Clay Minerals, 2004, 39(2): 135-149.
[7] SHARIFZADEH M, TARIFARD A, MORIDI M A. Time-dependent behavior of tunnel lining in weak rock mass based on displacement back analysis method[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2013, 38: 348-356.
[8] MOYA I, AGREDA E, MORALES E, et al. A review of expansive phenomena in Wagenburg North Tunnel[J]. Revista D La Academia Colombiana D Ciencias Exactas Fisicas Y Naturales, 2010, 33: 455-468.
[9] ANAGNOSTOU G . A model for swelling rock in tunnelling[J]. Rock Mechanics & Rock Engineering, 1993, 26(4): 307-331.
[10]BUTSCHER C , MUTSCHLER T, BLUM P. Swelling of clay-sulfate rocks: a review of processes and consols [J]. Rock Mechanics and Rock Engineering, 2016, 49(4): 1533-1549.
[11]钟祖良, 刘新荣, 王道良, 等. 桃树垭隧道底鼓发生机理与防治技术研究[J]. 岩土工程学报, 2012, 34(3): 471-476.
[12]师亚龙, 陈礼伟, 裴涛涛, 等. 软岩隧道底鼓机理及底鼓量计算方法[J]. 铁道建筑, 2014(5): 54-56.
[13]WITTKE-GATTERMANN P. Computation of strains and pressures for tunnels in swelling rocks[J]. Tunneling & Underground Space Technology, 2004, 19(4): 422-423.
[14]秦巴列維奇. 矿井支护[M]. 北京: 煤炭工业出版社, 1953: 98-696.
[15]李卫平. 地下水浮力计算和抗浮基础设计[J]. 江苏建筑, 2013(4): 78-83.
[16]高新强. 高水压山岭隧道衬砌水压力分布规律研究[D]. 成都:西南交通大学, 2005.
Calculation and Analysis of Track Bed Floating Characteristics
of Karst Tunnel Considering Water Basin Effect
Abstract:
Focusing on the problem of floating floor heave on the track bed of water-rich tunnel, this paper explores the introduction of water basin effect into the study of floating floor heave disease on the ballastless track bed of tunnels. Firstly, based on the strain energy and energy theory, combined with the contact mechanical conditions between structural layers, the stress and deformation of tunnel track bed are deduced to verify the rationality of the correlation between water basin effect and track bed floating. Secondly, the deformation deflection curve equation of track bed and the formula of stress and maximum deformation are constructed. It is obtained that the floating floor heave of track bed can cause bonding failure at the height of 0.5m water head, and the floating stage is divided into three stages by setting the critical water head value of floating: 1) initial infiltration catchment stage; 2) local ponding stage; 3) basin floating stage. Finally, the calculation formulas of horizontal and vertical floating amount of track bed under different drainage conditions are established, the curves of relationship between base water flow difference, pressure rate, floating rate and floating amount are formed, and the calculation method of minimum head height of tunnel track bed floating is constructed, so as to help the research of track bed floating control and the improvement of treatment measures.
Key words:
water-rich tunnel; ballast bed floating; basin effect; mechanical characteristics
