基于LM优化的车载全景影像绝对测量方法

曹君 叶辰萌 刘正华

摘 要：【目的】为解决车载全景影像在智慧城市、智慧城管、智慧交通等领域中应用不足的问题，提出了一种基于LM优化的车载序列全景影像绝对测量的方法。【方法】首先，对待测目标点在全景影像上的成像过程进行分析，详细推导了目标点绝对坐标测量的理论模型。其次，为解决该理论模型的优化求解问题，引入了对初值不敏感且收敛速度较快的LM算法，并对LM算法中的初值获取、函数构建、参数设置等问题进行了设计。最后，结合实际车载全景影像和目标点位实测数据，对所提的方法进行验证。【结果】该方法获得的目标点绝对坐标平面中误差和高程中误差分别为0.123 m和0.118 m，符合《城市测量规范》（CJJ/T 8—2011）中的相关要求。【结论】该方法能够有效获取全景影像范围内待测目标点的绝对坐标，从而为全景影像在城市部件普查、交通基础设施测量等领域的应用提供了可能。

关键词：LM优化；车载；全景影像；绝对测量

中图分类号：TP3     文献标志码：A      文章编号：1003-5168（2024）07-0005-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.07.001

Absolute Measurement Method Of Vehicle Panoramic Image Based On LM Optimization

CAO Jun1 YE Chenmeng1 LIU Zhenghua2

（1. Wuhan City Polytechnic， Wuhan 430064， China;

2. Institute of Seismology， China Earthquake Administration， Wuhan 430071， China）

Abstract： [Purposes] Aiming at the problem of insufficient application of vehicle panoramic images in the fields of smart city， smart city management， smart transportation， etc.， a method of absolute measurement of vehicle sequence panoramic images based on LM optimization is proposed. [Methods] Firstly，by analyzing the imaging process of the target point to be measured on the panoramic image， the theoretical model of the absolute coordinate measurement of the target point was deduced in detail. Secondly， in order to solve the optimization problem of the theoretical model， the LM algorithm， which is insensitive to the initial value and has a fast convergence speed， is introduced， and the initial value acquisition， function construction and parameter setting in the LM algorithm are designed. Finally， the proposed method is verified by combining the actual vehicle panoramic image and the measured data of the target point. [Findings] The results show that the mean square errors of the plane and elevation coordinates of the target points obtained by this method are 0.123 m and 0.118 m， respectively， which meet the relevant requirements in the'Urban Surveying Specification （CJJ/T 8—2011）'. [Conclusions] This method can effectively obtain the absolute coordinates of the target points to be measured in the range of panoramic images， thus providing the possibility for the application of panoramic images in the fields of urban component survey and transportation infrastructure measurement.

Keywords： LM optimization; vehicle; panoramic images; absolute measurement

0 引言

隨着计算机技术、通信技术、传感器技术、互联网技术的发展，利用多视点组合式相机获取后再经过图像拼接处理而形成的序列360°全景影像，以其全方位、沉浸式、高分辨率、场景真实等优点，被广泛应用于街景地图、公安应急、城市管理等领域［1-7］。

尽管现在拥有360°全方位景观表现能力，但是目前的全景影像却往往只有漫游、查询功能，不具备测量分析能力，极大地限制了其在城管部件普查、交通基础设施测量等领域的应用。近年来，基于全景影像的三维重建、位置获取、几何量测等问题研究逐渐兴起［8-17］。这些研究的原理大多数是共线条件方程、核线约束、光束法平差等传统摄影测量方法的推导与沿用，主要用于在局部坐標系下进行距离、面积、体积、变形监测等的相对测量，无法满足智慧城市、智慧城管、智慧交通等领域中获取目标绝对位置的需要。

因此本研究提出一种基于LM优化的车载序列全景影像绝对测量方法。该方法首先估计目标初始位置，并计算其在多张序列全景影像上的坐标；其次以计算坐标和实际坐标的差值构建目标函数；最后利用LM算法迭代优化，求解目标的最优点位。通过实验分析，证明了基于LM优化的全景影像绝对测量方法可以获取目标点在大地坐标系下的绝对坐标，满足城市测量的精度要求。

1 全景影像绝对测量模型

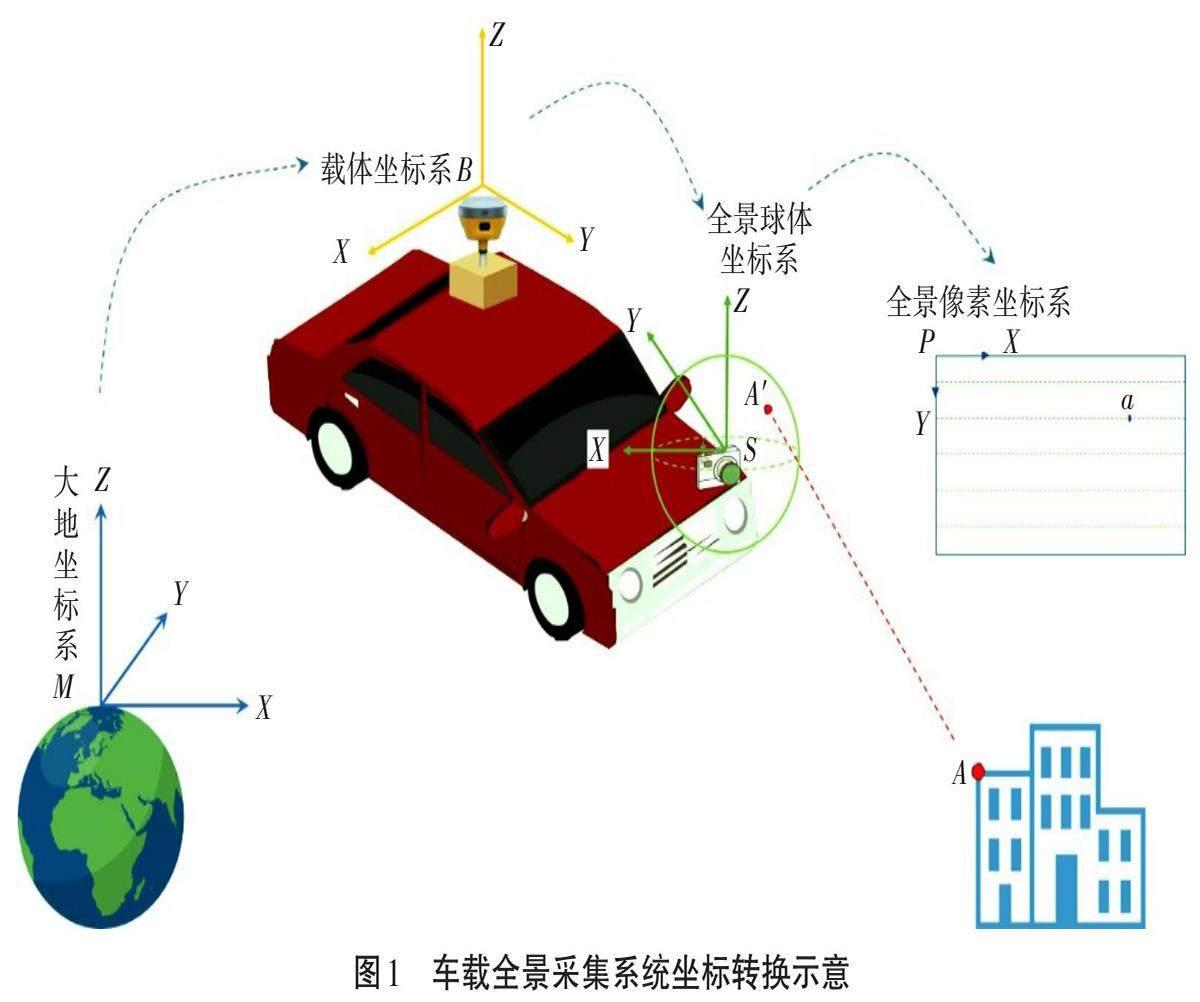
为快速获取连续序列全景影像数据，在数据采集过程中，通常需要将全景采集设备、定位定姿系统（Position and Orientation System，POS）、同步器等传感器集成安装在车辆等移动载体上，组成车载全景采集系统。在车辆行驶过程中，该系统连续采集全景影像数据，并同步记录各全景影像采集时车体的位置和姿态信息。

对上述序列全景影像成像范围内的目标点[A]，设其在大地坐标系下的绝对坐标为[（XMA，YMA，ZMA）]。为计算其在第[i]张序列全景影像上对应的像素坐标[a（uci，vci）]，需要经过一系列坐标转换：大地坐标系（M系）[→]à载体坐标系（B系）[→]à全景球体坐标系（S系）[→]à全景像素坐标系（P系），如图1所示。

目标点[A（XMA，YMA，ZMA）]在第[i]张序列全景影像对应像素坐标的计算过程，以如下两步完成。

1.1 计算全景球在大地坐标系M中的坐标和姿态

1.1.1 计算全景球体中心S在大地坐标系M中的位置，见式（1）。

[XMSYMSZMS=XMgYMgZMg+RMBXBSYBSZBS]     （1）

式中：[[XMgYMgZMg]] 为车载POS系统记录的成像瞬间车体在大地坐标系中的坐标值；[RMB]为载体坐标系B到大地坐标系M的旋转矩阵（可通过车载POS系统记录的成像瞬间车体姿态角获得）；[[XBSYBSZBS]]为全景球成像中心S在载体坐标系B中的坐标（可通过事先高精度检校获得）。

1.1.2  计算大地坐标系M到全景球体坐标系S的旋转矩阵，见式（2）。

[RSM=RBM×RSB]  （2）

式中：[RBM]为大地坐标系M到载体坐标系B的旋转矩阵（可通过车载POS记录的成像瞬间车体姿态角获得）；[RSB]为载体坐标系B到全景球体坐标系S的旋转矩阵（可通过事先高精度检校获得）。

1.2 计算点A在全景影像上的对应点a的像素坐标

1.2.1 计算点A在全景球体坐标系S中的坐标。对大地坐标系下的目标点[A（XMA，YMA，ZMA）]，其在全景球体坐标系中的位置及成像关系，如图2所示。

目标点[A（XMA，YMA，ZMA）]在以全景成像中心S为原点的空间直角坐标系中的坐标，见式（3）。

[XSAYSAZSA=RSM×（XMAYMAZMA-XMSYMSZMS）]  （3）

式中：[[XMAYMAZMA]]为点A在大地坐标系下的坐标值；[[XMSYMSZMS]]为全景球中心S在大地坐标系M中的位置；[RSM]为大地坐标系M到全景球体坐标系S的旋转矩阵。

获得点A在全景空间直角坐标系中的坐标后，需将点A投影至单位全景球面上，其对应的投影点A'的位置可以通过与X轴的夹角[φ]、与XSY平面的夹角[θ]来表示，见式（4）。

[φ=arccosXSA（XSA）2+（YSA）2θ=arcsinZSA（XSA）2+（YSA）2+（ZSA）2]  （4）

式中：[[XSAYSAZSA]]为目标点A在以全景成像中心S为原点的空间直角坐标系中的坐标。

1.2.2 计算点A在全景像素坐标系P中的坐标。由于全景球为一个三维球面，无法以图片的形式直接存储在计算机中，在实际存储过程中，需要对其进行降维处理，转化成便于存储的二维图片［18-19］，如图3所示。

全景球上的任一点A'，其在全景图像中对应的像素坐标，见式（5）。

[uc=imgW2+φ×imgW2πvc=imgH2-θ×imgHπ] （5）

式中：[imgW]、[imgH]分别表示全景影像宽度、高度；[φ]、[θ]表示A'在全景球体坐标系S中的位置。

2 目标绝对位置优化求解

2.1 目标初始位置估计

车辆行驶过程中连续采集的全景影像，通常各相邻影像间具有较大重叠度，即对于某观测目标点A，可在多张连续序列全景影像上被观测到。设点A在N张序列全景影像上可清晰成像，通过POS系统记录的各全景影像拍摄瞬间车体位置分别为[（X1 Y1 Z1）、（X2 Y2 Z2）…（XN YN ZN）]，则点A在大地坐标系中的初始位置[A（XMA，YMA，ZMA）]可通过将各个成像瞬间的车体位置取平均值的方式粗略估计，见式（6）。

[XMAYMAZMA=（X1+X2+…+XN）/N（Y1+Y2+…+YN）/N（Z1+Z2+…+ZN）/N] （6）

2.2 LM优化算法

由POS系统记录的车体位置按照公式（6）求出目标绝对位置的初值后，再利用公式（5）计算其分别在N张序列全景影像上的像素坐标，以在N张影像上计算得到的像素坐标与实际像素坐标之间差值的平方和最小来构建目标函数，见式（7）。

[F（X）=f（XMA，YMA，ZMA）=i=1N（uci-ui）2+（vci-vi）2] （7）

式中：[（uci，vci）]为第[i]张影像上目标点A的计算像素坐标，可通过公式（5）表达为关于点A在大地坐标系下的坐标值[（XMA，YMA，ZMA）]的函数；[（ui，vi）]分别为第[i]张影像上目标点A的实际像素坐标。

针对这一非线性目标函数的寻优问题，采用对初值不敏感且收敛速度较快的非线性优化算法（Levenberg-Marquardt，LM）。該算法集成了高斯牛顿法和梯度下降法两种算法的优点，通过控制改变阻尼因子变量的值，调节每次算法迭代的步长，从而有效提升迭代优化效率，实现对目标函数最小二乘法的优化。设[Xk]为第[k]次迭代求得的点A坐标，则对式（7）LM算法的步长，见式（8）。

[dk=-[J（Xk）TJ（Xk）+λkI]-1J（Xk）TF（Xk）]  （8）

式中：[J（Xk）]为目标函数的雅可比矩阵；[F（Xk）]为目标函数的值；[I]为单位矩阵；[λk]为阻尼因子。

将式（6）获得的点A粗略坐标作为初值，利用LM算法进行迭代计算，算法步骤［20］如下。

①输入初值[X0]，初始阻尼因子[λk=0.01]，初始迭代次数[k=0]，终止误差[ε=1×10-8]；

②计算[F（Xk）]、[J（Xk）]；

③计算步长[dk]，求解[Xk+1=Xk+dk]、[F（Xk+1）]、[J（Xk+1）]；

④若[F（Xk+1）≥F（Xk）]，则令[k=k+1]，[λk=10λk]，转入步骤③；

⑤若[F（Xk+1）

⑥若[F（Xk+1）

3 实验分析

为验证上述方法的有效性，本研究以一台经过系统检校的车载全景测量采集系统为数据获取平台，采集了一组外业全景影像数据及各影像采集瞬间的车体位置、姿态数据。在整个行车路线范围内选取了5组序列影像，每组4张连续全景影像，相邻影像间采集间隔约10 m。

在每组序列影像拍摄范围内分别选取一个目标点，按本研究的方法，依次进行初值获取、坐标转换和迭代优化，获取其大地坐标计算结果，并将计算结果与目标点的GNSS实地量测结果进行对比，结果见表1、表2。

4 结论

从上述结果可知，基于车载序列全景影像获取目标的绝对位置，其结果与GNSS实测结果相比，平面平均点位误差（绝对值）为0.111 m，平面中误差为0.123 m，高程平均误差（绝对值）为0.116 m，高程中误差为0.118 m，符合《城市测量规范》（CJJ/T 8—2011）中的相关要求。上述结果证实了本研究提出的方法能够有效获得全景影像范围内待测目标点的绝对坐标，从而为全景影像在城市部件普查、基础交通设施测量等领域的应用提供了可能。

参考文献：

［1］曹君，刘正华，洪勇，等.车载鱼眼图像的全景图拼接误差分析［J］.测绘科学，2016，41（7）：202-204，172.

［2］LI L，YAO J，XIE R P，et al.A unified framework for street-view panorama stitching［J］.Sensors，2016，17（1）：1-1.

［3］王志豪，侯辉娇子，田震.实景测量在智慧城管三维可视化中的应用［J］.测绘通报，2020（S1）：268-270.

［4］成功.IP-S2车载移动测量系统在数字城管信息系统中的应用［J］.测绘与空间地理信息，2017，40（9）：109-113.

［5］张伟朋，姚佩超，李文博.车载移动测量系统在城市街道整治中的应用［J］.测绘通报，2021（S2）：264-266.

［6］LIU Y Z，CHEN M X，WANG M H，et al.An interpretable machine learning framework for measuring urban perceptions from panoramic street view images［J］.iScience，2023，26（3）：106132-106132.

［7］周长江，杜洪涛，李欣，等.车载移动测量系统在智慧城市建设中的应用研究［J］.城市勘测，2023（2）：80-84.

［8］施并招，吕威.智慧城市街区虚拟全景影像三维快速重建研究［J］.计算机仿真，2021，38（7）：350-354.

［9］葛朋祥，王欢庆，朱奕磊，等.基于平面镜成像的单相机数字图像相关三维全景测量［J］.中国激光，2022，49（9）：92-100.

［10］凌家曜，钟平，吴靖，等.全景相机与PTZ相机联动监控系统及位置关联模型［J］.计算机应用与软件，2021，38（3）：202-209.

［11］刘昱谦.基于双目鱼眼镜头的全景成像及三维测量算法研究［D］.成都：电子科技大学，2021.

［12］郭伟青.基于镜面成像技术的单目全景立体感知三维重构技术研究［D］.杭州：浙江工业大学，2019.

［13］王启超，张维光，任永平.基于全景相机的3D坐标测量方法［J］.电子测量技术，2017，40（12）：203-208.

［14］梅文胜，胡帅朋，李谋思，等.基于普通数码相机的旋转全景摄影测量方法［J］.武汉大学学报（信息科学版），2017，42（2）：243-249.

［15］LI Y R，ZHAO D，MA X Y，et al.Panoramic digital image correlation for 360-deg full-field displacement measurement［J］.Applied Sciences，2023，13（3）：2019-2019.

［16］ZHU K Y，PAN B.Panoramic/dual-surface digital image correlation measurement using a single camera［J］.Sensors，2022，22（9）：3266-3266.

［17］JIANG S，WANG Y J，ZHANG J，et al.Full-field deformation measurement of structural nodes based on panoramic camera and deep learning-based tracking method［J］.Computers in Industry，2023，146.

［18］曹君，洪勇.车载鱼眼相机的间接法全景影像拼接［J］.地理空间信息，2016，14（10）：73-74，77，5.

［19］何林飞，朱煜，林家骏，等.基于球面空间匹配的双目鱼眼全景图像生成［J］.计算机应用与软件，2020，37（2）：166-170，239.

［20］李国民，宿梦瑶，朱代先.光束平差法中的一种改进LM算法［J］.西安科技大学学报，2022，42（1）：152-159.

收稿日期：2023-09-14

基金项目：湖北省教育厅科学研究计划项目（B2020425）；武汉市知识创新专项曙光计划项目（2023020201020480）。

作者简介：曹君（1987—），女，硕士，讲师，研究方向：地理信息分析与应用。