某型灭火飞机水箱晃动结构动响应分析

保鑫 郑永罡 秦浩 陈吉昌 童明波

基金项目：航空科学基金（20220023052001）

第一作者简介：保鑫（1998-），男，硕士，设计员。研究方向为流固耦合

*通信作者：童明波（1966-），男，博士，教授。研究方向为固体力学。

DOI：10.19981/j.CN23-1581/G3.2024.16.019

摘  要：灭火飞机工作过程中，灭火剂晃动会對水箱结构造成冲击及影响飞行稳定性。针对该问题，以某型灭火飞机水箱为研究对象，基于LS-DYNA建立FEM-SPH的流固耦合仿真模型，开展水箱灭火剂晃动的仿真分析。研究飞机在起飞阶段，不同充液时水箱结构的动态响应、液体重心变化大小及防晃板的抑制作用，为该型飞机综合航电灭火平台基本型水箱设计提供有效的计算分析数据及优化建议。

关键词：灭火飞机；水箱晃动；流固耦合；FEM-SPH；仿真模型

中图分类号：V271.3+8 文献标志码：A         文章编号：2095-2945（2024）16-0082-05

Abstract： In the working process of fire-fighting aircraft， the sloshing of fire-extinguishing agent will have an impact on the structure of water tank and affect the flight stability. In order to solve this problem， taking the water tank of a fire extinguishing aircraft as the research object， the fluid-structure coupling simulation model of FEM-SPH is established based on LS-DYNA， and the simulation analysis of water tank fire extinguishing agent sloshing is carried out. The dynamic response of the water tank structure， the change of the liquid center of gravity and the inhibition of the anti-sloshing plate during the take-off stage of the aircraft are studied in order to provide effective calculation and analysis data and optimization suggestions for the basic water tank design of the integrated avionics fire extinguishing platform of this type of aircraft.

Keywords： fire-fighting aircraft; water tank sloshing; fluid-structure coupling; FEM-SPH; simulation model

灭火飞机在面对自然灾害时固然发挥重要作用，但在起飞、降落或实现飞行任务过程中，水箱内灭火剂的剧烈晃动会对水箱造成比较严重的冲击载荷，同时晃动灭火剂会改变飞机的重心，进而影响飞机的飞行稳定性。灭火剂大幅晃动产生的作用力会影响飞机的飞行姿态，同时，飞行姿态的变化又会加剧灭火剂的晃动，交互耦合可能会导致飞机失稳，威胁到飞行安全，因此有必要进行水箱晃动分析。

灭火飞机水箱晃动与飞机油箱晃动问题类似，早期对晃动问题的研究主要以理论研究和试验研究为主，理论研究一般针对具体情况作出相应的假设，来求解问题，试验研究的对象主要为简单结构的容器。随着研究深入和计算水平的提高，数值研究方法成为液体晃动问题的重要手段，对于复杂的结构及晃动条件，数值方法能有效仿真液体晃动的流固耦合问题，节省资源的同时能保证一定的精度，数值研究方法成为研究液体晃动问题的重要手段。

Hosain等[1]针对液化天然气在液舱中晃动对结构的影响，基于雷诺平均纳维尔-斯托克斯方程（RANS）的计算流体动力学（CFD），采用流体体积（VOF）方法和光滑粒子流体动力学（SPH）方法，在二维及三维尺度上进行仿真模拟，与试验结果进行对比验证。表明了2种方法在流体动力、压力、力方面的准确性，以及证明SPH方法在捕捉晃动现象方面的能力。Pilloton等[2]对船舶LNG燃料箱内的晃动流动进行了数值研究。采用SPH方法进行真实海况模拟，考虑了3种不同的充液比，并进行仿真模拟结果与试验结果的比较，证明数值模拟方法能提供良好的局部压力估计效果。刘富[3]结合飞机副油箱晃动试验，采用SPH方法对菱形液舱进行了晃动分析，并与试验结果对比，同时探讨了贮箱充液比、晃动周期及晃动振幅对贮箱壁压力的影响。邹喜聪[4]采用SPH方法对飞机机身燃油晃动进行了分析，研究了不同充液高度和不同速度载荷激励下的晃动响应，同时对安装防晃挡板后的晃动情况进行了模拟，研究挡板在油液晃动中的防晃作用。杜林霏[5]采用C语言编程建立了传统SPH方法的求解程序，并针对大幅晃动问题采用数值计算方面的改进方法，以实际工程应用为研究对象，进行数值计算求解并给出了相关的设计建议。钟连等[6]基于Abaqus与Star-ccm+联合的单向流固耦合方法，完成飞机在弹射和拦阻大机动过载下的油箱晃动动响应分析。

针对以上问题，本文基于LS-DYNA软件[7]，采用FEM-SPH流固耦合方法模拟水箱灭火剂晃动，以某型灭火飞机水箱为研究对象，建立飞机水箱晃动的数值仿真模型，探究飞机在急停刹车运动状态下的水箱灭火剂晃动对水箱结构的影响，为研究灭火飞机水箱结构设计提供参考。

1  数值计算方法

SPH方法通过构造一个近似场函数来表示粒子的速度和能量，函数的粒子近似为

，    （1）

式中：h为定义核函数W的影响区域的光滑长度；？赘为包含x的积分体积。

根据核函数W（x-x′，h）的定义，其具有以下性质

式中：？啄（x-x′）为狄拉克函数。这些性质保证了在连续体极限内适当的归一化和一致性。

可以构造多种不同种类的光滑函数。常用的函数有高斯核函数，三次、四次、五次样条核函数，二次核函数（Johnson[8]；用于模拟高速撞击）。在软件LS-DYNA中采用如下三次B样条光滑函数

式中：d为空间维度的数目（2或者3）；？兹（x）是三次B样条函数，定义为

， （4）

式中：C为标准化的常数，取决于空间维度的数量。函数？兹（x）的曲线图如图1所示。

图1  LS-DYNA中的一维样条函数

SPH公式的第二个关键步骤是粒子近似，使得支持域可由有限数量的粒子表示。连续积分表示可以转换为离散形式，即半径为？资h的支持域中所有粒子的叠加求和。粒子i处的粒子近似可以写成

式中：？籽j为粒子j的密度；mj为位于j处的粒子质量。Wij=W（xi-xj，h），是以粒子i为中心，在粒子j处求值的光滑核函数。

因此，粒子i的值可以用粒子i的支持域内所有粒子的函数值的加权平均值来近似。对上式两边求导，得到i处的函数空间导数粒子近似

其中

由以上公式可以看出，SPH方法使用粒子来进行计算，将粒子近似式函数及其导数的连续积分离散，因此粒子之间不需连通，从而实现了无网格化。

2  水箱建模

2.1  FEM-SPH方法验证

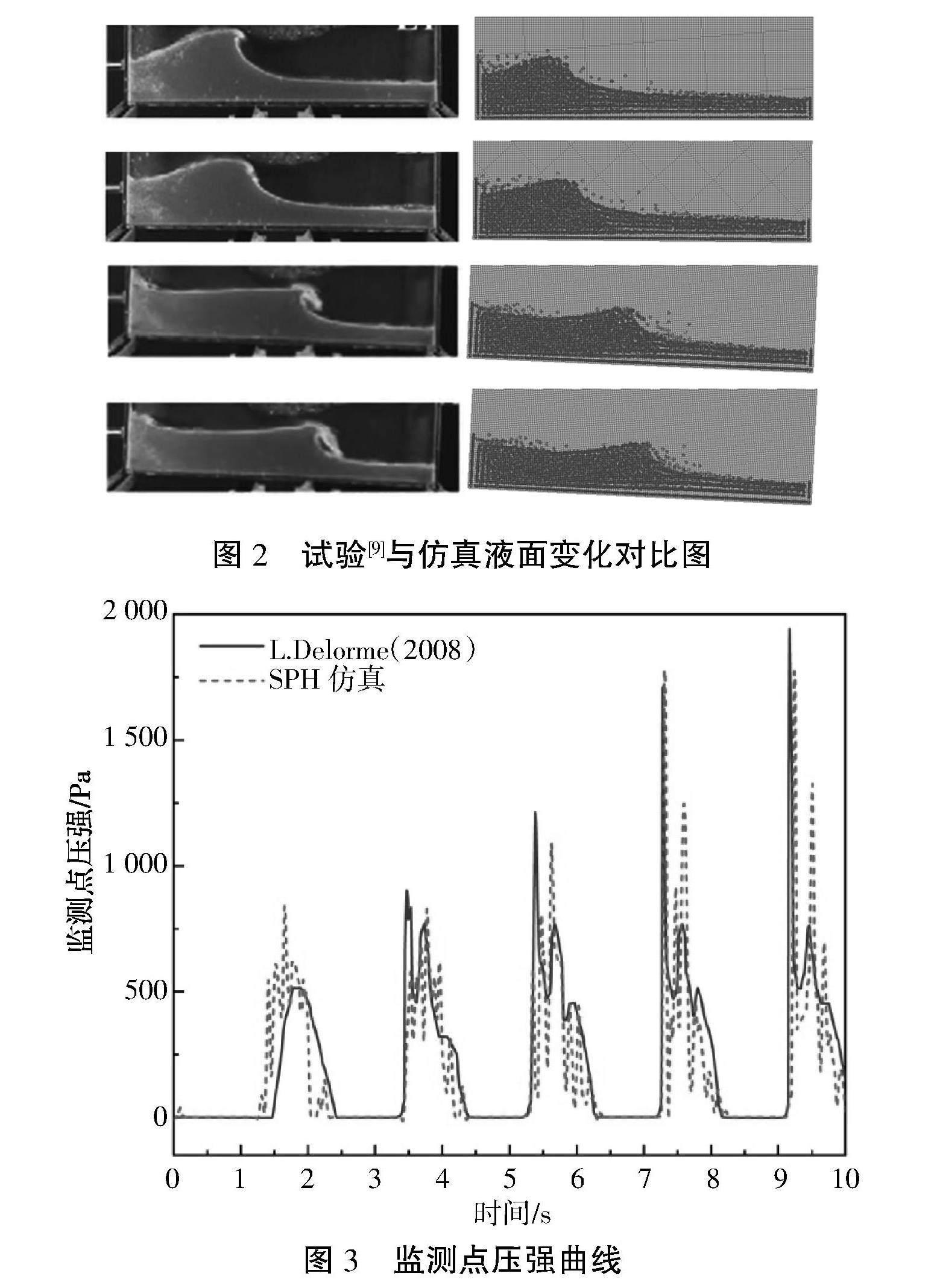
本文基于LS-DYNA进行FEM-SPH的流固耦合计算，通过流场压力的单向传递进行结构响应的求解，为验证算法的可靠性，建立算例与Delorme等[9]的试验结果对比。试验中，矩形贮箱绕底面中轴作正弦周期晃动，角位移？兹=？兹maxsin2？仔ft（f=1/T），f为频率，T为周期。贮箱尺寸为980 mm×580 mm×50 mm（长×高×宽），充液高度93 mm，贮箱内介质为水和空气。选择晃动幅度？兹max=4°，晃动周期T=1.92 s工況进行模拟，计算了5个晃动周期，结构域壁面视为刚性。如图2所示，其为贮箱左壁第1次冲击过后出现的液面行进形态，可见模拟与试验得到的行进波形态极为相似。对于贮箱液体晃动问题，SPH方法只考虑液体与结构的相互作用，而忽略了空气的影响，仿真结果与试验现象在液体表面的波浪只存在细微差异。对于壁面压强结果来说，SHP仿真结果与试验结果吻合较好，每次冲击产生的压强峰值相近，证明SPH方法能够很好地模拟液体晃动现象，如图3所示。

图2  试验[9]与仿真液面变化对比图

图3  监测点压强曲线

2.2  数值仿真模型

该灭火飞机配备4个水箱，每个水箱最大装载1.5 t液体灭火剂，取其中一个水箱进行建模分析。水箱由5块壁板、防晃板及内部的桁架结构组成，整体结构如图4所示，水箱结构采用铝合金材料，具体材料参数见表1。

对水箱CAD模型进行完几何清理后，进行水箱的精细化网格划分，由于水箱为薄壁板杆结构，因此水箱结构均采用壳单元划分，内部液体灭火剂采用SPH粒子离散，零部件之间采用1-D单元模拟铆钉连接，且不考虑铆钉单元的失效。水箱结构网格尺寸为10 mm，壳单元数量为149 839，粒子间距为结构单元尺寸的2倍，既保证了计算结果的准确性，也能节省计算资源。

图4  整体水箱数值模型

表1  水箱结构材料参数

2.3  仿真工况

飞机在起飞着陆阶段机体晃动较为剧烈，考虑灭火飞机真实起飞阶段对水箱晃动的影响，探究水箱在不同充液比下的晃动情况，分别设置25%、50%、75%充液比进行计算，不同充液比水箱数值模型如图5所示。同时，考虑有无防晃板对液体晃动幅度的影响，工况说明见表2。

（a）  25%         （b）  50%        （c）  75%

图5  不同充液比水箱数值模型示意图

表2  水箱晃动工况表

3  结果分析

3.1  不同充液比水箱结构动响应分析

在飞机起飞阶段，由于惯性作用，灭火剂晃动，水箱结构受到较大冲击载荷，有必要进行水箱结构动响应分析。对比分析工况一、二、三计算结果，见表3。

表3  水箱结构最大Mises应力

由表3可知，水箱结构应力水平较低，最大应力主要发生在蒙皮各壁板之间弯曲过渡位置及侧壁板1底部竖梁和角片位置，这些结构为主要承力及灭火剂冲击部位，最大应力发生位置如图6所示。

图6  水箱蒙皮及桁架结构最大应力云图

3.2  灭火剂重心变化分析

对比不同充液比下，灭火剂在X方向（航向）、Y方向（垂向）的重心变化趋势及幅度。由图7可知，随着充液量增加，沿X方向的灭火剂重心变化明显减小，沿Y方向的灭火剂重心变化逐渐增大。在该运动状态下，不同充液比灭火剂重心相对变化曲线的变化趋势大体一致，重心变化峰值有所变化。灭火剂重心在X方向（航向）变化峰值最大为63 mm，Y方向（垂向）重心变化峰值最大为29 mm。

由以上结果对比分析可知，在该飞行状态下，X方向灭火剂晃动幅度较大，尤其是低充液比状态下。在大充液比状态下，防晃板对于灭火剂在X方向的抑制作用明显，若灭火剂充液量较小，初始状态灭火剂与防晃板无接触，因此防晃板几乎没有抑制液体晃动的作用。

对于50%和75%充液比的灭火剂晃动来说，防晃板起到一定的抑制晃动作用，如图8所示，其为灭火剂在X方向（航向）、Y方向（垂向）的重心变化趋势及幅度。由图8可知，在该飞行工况下，防晃板最大起到22%的防晃作用。对于充液比为50%的Y方向（垂向）的防晃作用较小，而且50%充液比时，防晃板只有小部分结构与灭火剂接触，对于50%充液比的灭火剂防晃效能不佳，与防晃板的安装位置、方向等有关。

（a）  航向曲线图

（b）  垂向曲线图

图7  不同充液比灭火剂重心变化曲线图

（a）  航向曲线图

（b）  垂向曲线图

图8  有无防晃板灭火剂重心变化曲线图

4  结束语

基于LS-DYNA软件建立流固耦合数值模型，计算某型灭火飞机在起飞阶段的水箱灭火剂晃动问题，探究结构动响应與灭火剂重心变化规律，得出以下结论。

1）飞机起飞阶段水箱灭火剂晃动幅度相对航行状态晃动幅度较大，但灭火剂晃动冲击作用下的水箱结构应力水平远低于材料的屈服强度，结构不会发生破坏。长期的冲击作用下水箱结构已发生泄漏、气密性降低等情况，仍需考核易发生结构破坏的位置。

2）随着充液比增加，水箱结构的大部分区域应力峰值也相应增大，但壁板弯曲过度位置及桁架结构角片和竖梁应力相对较大，长期冲击作用下结构的强度及可靠性降低，是重点考核对象。

3）防晃板对于高充液比的防晃效果明显，最大起到22%的防晃作用。对比有无防晃板的液体晃动情况，低充液比的防晃效果不明显，水箱灭火剂的防晃结构有优化空间。

参考文献：

[1] HOSAIN M L， SAND U， FDHILA R B. Numerical investigation of liquid sloshing in carrier ship fuel tanks[J]. IFAC-PapersOnLine， 2018，51（2）：583-588.

[2] PILLOTON C， BARDAZZI A， COLAGROSSI A， et al. SPH method for long-time simulations of sloshing flows in LNG tanks[J]. European Journal of Mechanics-B/Fluids， 2022，93：65-92.

[3] 刘富.贮箱内液体晃动动力学分析及结构防晃技术研究[D]. 南京：南京航空航天大学，2010.

[4] 邹喜聪.飞机机身油箱燃油晃动分析[D].哈尔滨：哈尔滨工业大学，2012.

[5] 杜林霏.基于SPH方法的航天器贮箱液体晃动动力学研究[D].北京：清华大学，2015.

[6] 钟连，支亚非，杨莹，等.大过载机动下飞机油箱晃动冲击效应的流固耦合分析[J/OL].应用力学学报，1-15[2024-05-16].http：//kns.cnki.net/kcms/detail/61.1112.O3.20230508.1216.004.html.

[7] LS-DYNA■ Keyword User's Manual， Version 971. Livermore Software Technology Corporation（LSTC）： Livermore， CA 94551-5110， USA， May 2007[Z].

[8] Johnson G R. SPH for high velocity impact computations[J]. Computer methods in applied mechanics and engineering，1996，139：347-373.

[9] DELORME L， COLAGROSSI A， SOUTO-IGLESIAS A， et al. A set of canonical problems in sloshing， Part I： Pressure field in forced roll-comparison between experimental results and SPH[J]. Ocean Engineering， 2009，36（2）：168-178.