基于WPA-Prophet模型的区域用电量预测

谭曾盛 王志兵

收稿日期：2023-09-13

DOI：10.19850/j.cnki.2096-4706.2024.06.028

摘  要：为了获得精度更高的用电量预测模型，采用狼群算法对Prophet模型的关键参数进行寻优，构建基于WPA优化Prophet的用电量预测模型。实验数据为澳大利亚维多利亚州2015—2019年五年的日用电量，使用前四年作为测试集，最后一年验证预测结果的准确性，预测结果的评价指标采用均方根误差和平均绝对百分比误差。实验结果表明，通过WPA优化后的Prophet模型预测精度得到了有效提升，为提升区域用电量预测精度提供了参考。

关键词：Prophet模型；狼群算法；用电量预测；时间序列

中图分类号：TP18    文献标识码：A 文章编号：2096-4706（2024）06-0132-04

Prediction of Regional Electricity Consumption Based on WPA-Prophet Model

TAN Zengsheng， WANG Zhibing

（College of Computer Science， Hunan University of Technology， Zhuzhou  412007， China）

Abstract： In order to obtain a more accurate electricity consumption prediction model， Wolf Pack Algorithm （WPA） is used to optimize key parameters of the Prophet model， and an optimized electricity consumption prediction model is built based on WPA. The experimental data is the daily electricity consumption of Victoria， Australia from 2015 to 2019. The data of first four years are used as the test set， and the accuracy of the prediction results is verified in the last year. The evaluation indexes of the prediction results are Root-Mean-Square Error and Mean Absolute Percentage Error. The experimental results show that the prediction accuracy of Prophet model optimized by WPA algorithm has been effectively improved， which provides a reference for improving the prediction accuracy of regional electricity consumption.

Keywords： Prophet model; Wolf Pack Algorithm; electricity consumption prediction; time series

0  引  言

现代经济的发展离不开电力行业的贡献，随着科技和经济的发展，对电力的需求将会不断增加。在2022年四川省因电力资源短缺实行了限电策略，造成了大批企业停工停产，低估电力需求会对社会的生产生活造成严重影响。而对于产生了而未被消耗的电能目前还没有大规模且具有普适性的电能储存方案，高估电力需求不可避免地会产生浪费；同时，火电发电量占总发电量的70%，避免电能浪费也能在一定程度上减少因火力发电而造成的环境污染。因此，对用电需求进行准确的预测对保障民生和促进社会经济发展都有重要意义。

用电量预测的方法大致可以分为传统时间序列模型和人工智能神经网络模型两种方法。传统的时间序列模型有Holt-Winters、ARMA/ARIMA等[1]，郭松亮等人[2]构建ARIMA模型对北京2019—2021年的用电量进行预测，实验的拟合误差在合理范围内，实验结果表明北京市的用电量将进一步增长。陈云浩等人[3]提出基于ARMA模型和Holt-Winters模型的組合模型方法，对中山某企业30天的用电量进行预测，实验结果显示模型预测的准确度较高，有一定的实用价值。人工智能不需要考虑数据的分布特征、能够刻画模型的非线性关系，在用电量预测方面有广泛应用[4]。成贵学等人[5]提出一种基于用电特性聚类和ConvLSTM相结合的企业用电量预测方法，有效地提取了用电数据特征，提高了预测精度。

缪庆庆[6]等人构建BP神经网络模型预测家庭用电量，通过调整神经元的权值降低了预测误差，实验结果对掌握居民的用电规律有一定帮助。除了传统的时间序列模型和神经网络模型，Facebook开源的基于时间序列分解的Prophet模型也能应用在用电量预测中，陆圣芝等人[7]构建Prophet模型预测某县的建筑、餐饮和住宿行业的用电量，实验结果表明，Prophet模型较传统时间预测预测模型精度更高。Prophet模型具有拟合速度快，可解释性强等特点，因此广泛应用于多个领域，但模型的参数设置不合理会导致模型的预测效果差。对此，本文提出一种基于狼群算法的Prophet预测模型参数优化方法，并应用在用电量预测中，实验表明，参数优化后的Prophet模型的预测精度得到了有效的提升。

1  算法基本原理

1.1  Prophet模型

Prophet模型是由Facebook团队开源的时间序列预测模型[8]。相较于传统的统计学模型，Prophet 模型的灵活性更强，可以根据时间序列的季节性变化做出更精准的预测，并且针对缺失的数据会进行自动处理[9]。与机器学习模型对比，Prophet模型的拟合速度更快，且模型具有可解释性。Prophet模型组成：

（1）

式中：g（t）表示趋势函数，用于分析时间序列在非周期性的变化趋势；s（t）表示季节函数，表示时间序列以日，周，月等周期性变化；h（t）表示节假日函数，用来表示节假日因素对时间序列的影响；?（t）表示误差。

趋势函数g（t）有两种结构，分别是分段线性趋势模型和饱和增长模型，本文使用的分段線性模型如式（2）所示：

（2）

式中：k表示模型的增长率；a（t）表示阶跃函数；δ表示k的变化量；m表示偏移量；γ表示使函数平滑的偏移量。

季节函数s（t）是使用傅里叶级数来表示模型的周期性变化，如式（3）所示：

（3）

式中：P表示季节性的周期大小，周期为年时，P为365.25，周期为周时，P为7；σ的数值可以控制季节性对预测模型的影响力，σ越大模型受季节性的影响越大。

节假日函数h（t）如式（4）所示：

（4）

式中：ki表示节假日的影响范围；L表示输入的节假日总个数。

模型的组成部分有相应的参数可以调节，changepoint_prior_scale这项参数可以调节增长趋势模型组件的灵活度，参数数值越大模型对历史数据的拟合程度越强，但是数值太大也有过拟合的风险。seasonality_prior_scale可以调节季节性模型组件的灵活度。参数数值越大，模型将适应更强的季节性波动，值越小，季节性波动越小。holidays_prior_scale调节节假日模型组件的灵活度，值越大，节假日项对模型的影响越大。默认的参数设置无法充分发挥模型的优势，模型的预测精度不佳，changepoint_prior_scale，seasonality_prior_scale，holidays_prior_scale等参数的合理取值是Prophet模型构建的关键。

1.2  WPA-Prophet模型构建

狼群算法（Wolf Pack Algorithm， WPA）是一种群体智能算法，和经典的粒子群及遗传算法相比，狼群算法的性能更优，更适合求解高维的复杂函数求解[10]。狼群算法思想基于狼群的群体智能行为，模拟了狼群在猎捕猎物时的捕食行为和猎物的分配方式。狼群有着明确的社会分工，狼群中的头狼作为首领，它是通过弱肉强食的竞争中胜出的，它主要负责狼群的指挥，而探狼主要负责搜寻猎物，猛狼则负责攻击[11]。

定义狼群的猎场是一个N×D的空间，N表示狼群的数量，D表示寻优参数的个数。狼群中的狼感知的气味浓度为Y = f （x），Y即为适应度值。通过强者生存的规则，在一轮轮竞争中最终生存下来的头狼，其Y值也就是最优的适应度值，表示为Ylead。狼群的猎捕活动可以抽象成三个具体的行为：

1）游走行为。探狼的初始适应度值为Yi，探狼朝h个方向移动，每个方向移动的步数为stepa，移动后在d维空间的的新位置为：

（5）

移动到新位置后重新计算新的适应度值为Yip，如果此时适应度值优于移动前位置的适应度值Yi，则更新探狼的位置并将新的适应度值Yip赋给Yi。如果Yi＞Ylead，则探狼将会替头狼发起召唤行为，否则将一直重复游走直到达到最大迭代次数Tmax。

2）召唤行为。头狼召唤周围的猛狼向头狼所在的位置靠近，移动的步长为stepb，猛狼i在k+1次迭代后在d维空间的新位置为：

（6）

式中： 表示第k次迭代时头狼在空间中的位置。

猛狼移动后位置的适应度值为Yi，如果此时Yi＞Ylead，那么此时猛狼就会转换为头狼并通过召唤行为召唤其他的猛狼靠近，否则猛狼会继续向头狼靠近。当猛狼和头狼的距离小于dnear，dnear如式（7）所示，则发起围攻行为。

（7）

式中：ω表示距离判定因子，ω的值会影响算法的收敛速度。

3）围攻行为。移动后的猛狼靠近了头狼，这时将联合探狼一起攻击头狼所在位置处的猎物，猎物在d维空间的位置为  ，围攻行为表示如下：

（8）

式中：λ表示一定范围内的随机数；stepc表示狼在围攻行为时的攻击步长。

如果在围攻行为后猎物所在位置的适应度值大于原位置的适应度值，则更新此狼的位置，否则位置不变。

在三种行为中，stepa、stepb、stepc三者的关系为：

（9）

式中：S表示步长因子，代表寻优的解的精细程度。

WPA算法求解Prophet模型最优参数具体步骤如下：

1）将用电量数据分为训练集和测试集，训练集用于预测模型训练，测试集用于检验模型的预测精度。

2）Prophet模型的changepoint_prior_scale参数默认设置为0.05，seasonality_prior_scale参数默认设置为10.0，holidays_prior_scale参数默认设置为10.0。将模型预测结果的平均绝对误差（MAE）作为适应度函数的值。

3）设置WPA的参数，其中最大迭代次数设置为100。

4）开始迭代，对Prophet模型的三个关键参数进行寻优，满足迭代次数后输出最优适应度值时的模型参数值。

5）根据输出的最优参数最终构建WPA优化后的Prophet模型，对测试集进行测试。

通过上述步骤即可得到WPA算法优化后的Prophet模型。

2  实验验证和结果分析

2.1  数据集来源

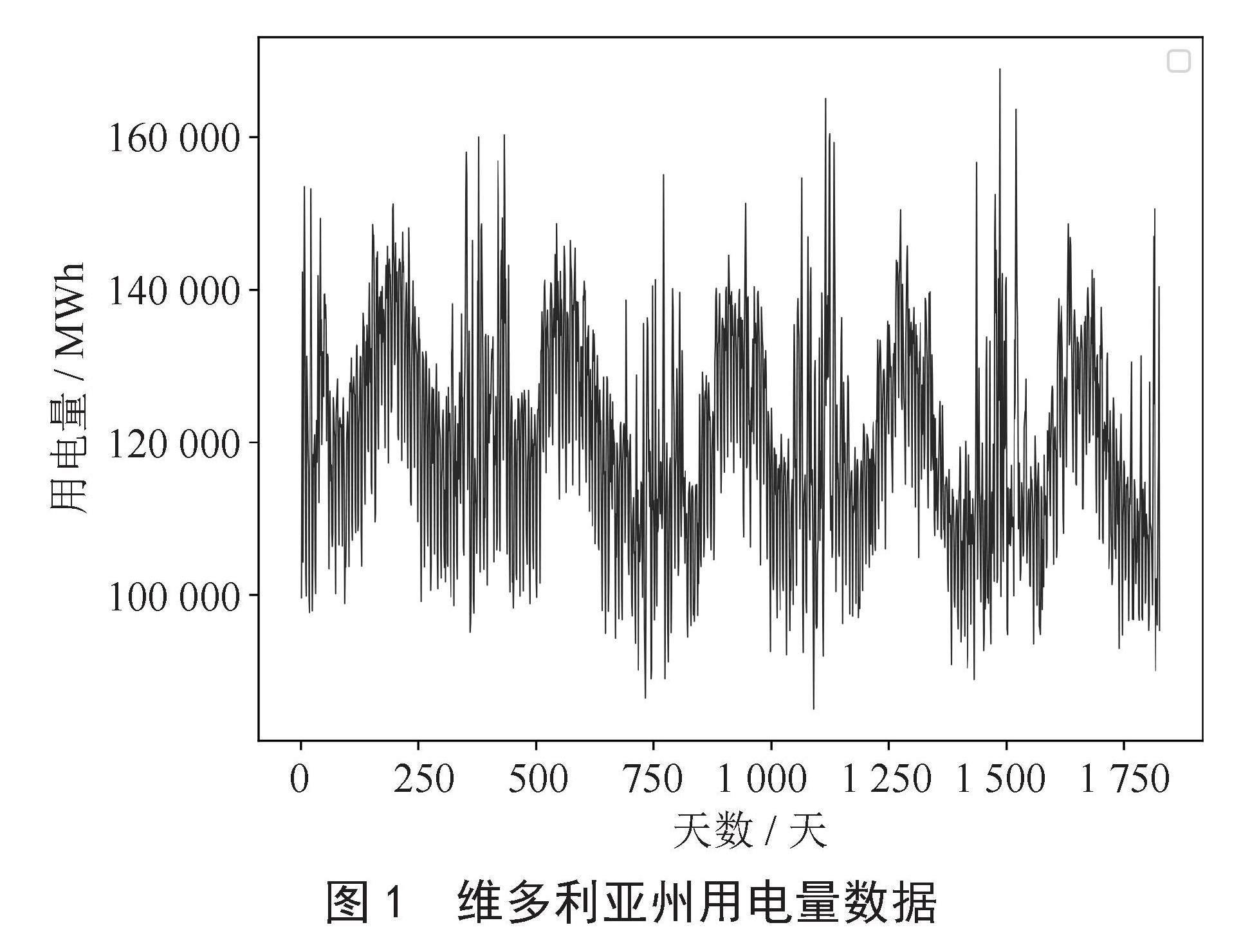
实验所用数据集来自Kaggle平台，数据集内包含澳大利亚第二大州维多利亚州2015年1月1日至2019年12月31日的用电量数据，数据粒度为天，共1 826条，如图1所示，从图中可以看出用电量数据具有明显的周期性。本实验将2015年1月1日至2018年12月31日共1 461条用电量数据作为测试集，预测未来一年的每日用电量，将2019年1月1日至2019年12月31日共365条用电量数据作为验证集。

图1  维多利亚州用电量数据

2.2  评价指标

本实验的评估方法采用均方根误差（RMSE）和平均绝对百分比误差（MAPE），综合两种评价指标对模型的預测结果进行全面分析。两种误差值越小，表示模型的预测效果越好。

2.3  Prophet模型预测结果

对用电量测试集构建Prophet模型，三个关键参数使用默认值，其中模型若要考虑节假日的影响，需要将有可能影响到预测结果的节假日输入holiday模块中，通过网站查询澳大利亚维多利亚州的节假日并将节假日的具体日期输入模型中。将2015年到2018年的用电量数据输入，预测未来365天的用电量数据。

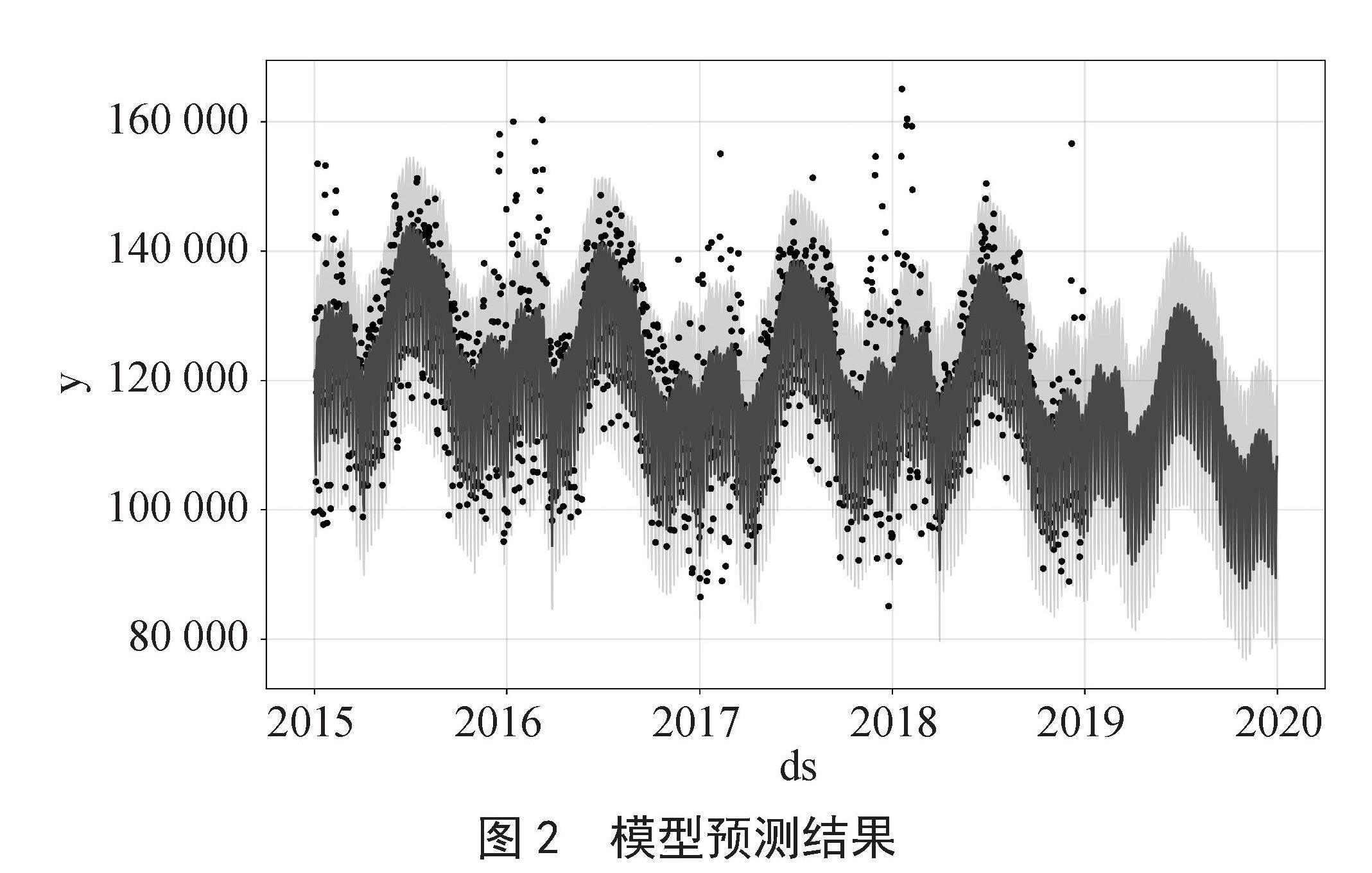
模型的最终预测结果如图2所示，图中黑点为实测值，蓝色线条为拟合曲线，最终预测结果的RMSE为10 845.78，MAPE为6.40%。

图2  模型预测结果

2.4  WPA-Prophet预测结果与对比分析

WPA算法迭代过程中变化的适应度值是Prophet模型预测的平均绝对误差值，在迭代寻优的过程中WPA的适应度值不断降低，在迭代次数大约为40次时，适应度值趋于稳定，此时已经找到最优解，所得到的最优解的平均绝对误差为0.054 7，得到最优解时Prophet模型的changepoint_prior_scale参数值为0.005，seasonality_prior_scale参数值为7.17，holidays_prior_scale参数值为1.02。

将所得最优解的模型参数重新构建Prophet模型，新构建的WPA-Prophet模型预测效果如图3所示，模型预测了2019年1月1日到2019年12月31日共365天的用电量。图中黑色虚线为用电量的实际值，绿色实线为WPA优化前的Prophet模型预测结果，红色实线为WPA算法优化后的Prophet模型预测结果，从图3中可以看出WPA优化后Prophet模型预测结果与实际值拟合度更高，预测效果优于未优化的Prophet模型。

图3  用电量预测效果对比

模型预测评估指标使用了RMSE和MAPE，值越小代表预测结果与实际值误差越小，预测结果越准确。两种模型的具体误差值如表1所示，WPA-Prophet模型的RMSE为9 564.52，相对于Prophet模型降低了1 281.26。WPA-Prophet 模型的MAPE为6.40%，相对于Propeht模型降低了0.93%。WPA-Prophet模型的两种误差评价指标都小于Prophet模型，说明WPA-Prophet模型在预测精准度上优于Prophet模型。

表1  不同模型预测评估指标

模型 RMSE MAPE

Prophet 10 845.78 6.40%

WPA-Prophet 9 564.52 5.47%

3  结  论

为了提高用电量预测的精度，本文提出一种基于WPA优化Propeht模型的用电量预测算法。对于Prophet模型参数设置不合理导致预测精度不理想的问题，采用WPA算法进行参数寻优，这样能够有效避免人为选择Prophet模型参数或者采用默认参数从而导致预测效果不理想。实验使用了澳大利亚维多利亚州2015—2019年用电量数据，使用前四年的数据作为测试集，预测维多利亚州2019年全年的用电量，实验结果显示，WPA优化后的Prophet模型的预测结果与真实值的拟合度高于未优化的Prophet模型，同时，通过WPA优化的Prophet模型的RMSE和MAPE分别下降了1 281.26和0.93%，说明模型的预测精度得到了有效提升。

参考文献：

[1] 闵旭，叶青，蔡高琰.基于残差自回归方法的短期区域用电量预测 [J].技术经济，2019，38（6）：119-124.

[2] 郭松亮，闫鹏君，鄂浩坤.基于ARIMA模型的北京市全社会用电量短期预测 [J].北京信息科技大学学报：自然科学版，2020，35（5）：93-96.

[3] 陈云浩，周冬.ARMA模型和Holt-Winters指数平滑模型在企业用电量预测中的应用与分析 [J].资源信息与工程，2021，36（4）：131-136.

[4] 王毅蕾，梁龙跃，蔡铉烨.基于人工神经网络的贵州省用电量预测 [J].生产力研究，2020（12）：96-98+160.

[5] 成贵学，乔臻，滕予非，等.基于电力数据挖掘的涉污企业用电量预测方法研究 [J].现代电子技术，2022，45（15）：151-156.

[6] 缪庆庆，林涛，张海静，等.基于BP 神经网络的家庭用电量预测与分析 [J].现代建筑电气，2020，11（10）：14-17+22.

[7] 陆圣芝，金诚，卜广峰，等.基于Prophet模型的电量预测技术研究 [J].机电信息，2020（18）：32-33.

[8] 刘铭基，田雅楠，张亮，等.基于Prophet-ARIMA模型的民航周转量预测研究 [J].计算机技术与发展，2022，32（2）：148-153+160.

[9] 李卿，罗佳.基于Prophet与LightGBM气象特征优化模型的短时机场飞行流量预测 [J].软件导刊，2023，22（8）：111-116.

[10] 朱颢.基于狼群算法的同时取送货模糊绿色车辆路径问题 [J].物流科技，2023，46（22）：109-115.

[11] 余泽泰，余盟，肖人彬，等.一种具有动态适应性的狼群算法及其应用 [J].河北工业大学学报，2021，50（3）：1-15.

作者简介：谭曾盛（1999—），男，汉族，湖南株洲人，硕士在读，研究方向：工业大数据；王志兵（1974—），男，汉族，湖南邵东人，副教授，硕士，研究方向：工业互联网、可信软件、知识图谱。