连续时间量子行走算法在截断单形晶格上的搜索研究

朱轩民 张德政

收稿日期：2023-11-06

DOI：10.19850/j.cnki.2096-4706.2024.06.017

摘  要：为证明连续时间量子行走算法在结构型数据库上的搜索可以实现二次加速的效果，对结构型数据库中的截断单形晶格类型，进行了连续时间量子行走算法的应用研究。首先对截断单形晶格进行对称性分析，确定系统演化所处的希尔伯特空间，然后用哈密顿量本征态与基础态的平方叠加、和简并微扰理论两种方法来求解系统演化需要的临界跳跃率。最后通过对图中的边进行加权的方法，合并了量子搜索的步骤，缩短了系统演化的时间，从而实现了平方加速的效果，并表明了边的权重对量子搜索过程的影响。

关键词：量子计算；量子搜索；连续时间量子行走算法；结构型数据库

中图分类号：TP391    文献标识码：A  文章编号：2096-4706（2024）06-0074-05

Research on Continuous-time Quantum Walk Algorithm Searching on Truncated Simplex Lattices

ZHU Xuanmin， ZHANG Dezheng

（Guizhou University of Finance and Economics， Guiyang  550025， China）

Abstract： To demonstrate the quadratic speedup effect of the continuous-time quantum walk algorithm searching in structural database， this study delves into its application specifically for the truncated simplex lattice within structural databases. Initially， the determination of the Hilbert space in which the system evolves is based on an analysis of the symmetry of the truncated simplex lattice. Subsequently， the critical jumping rate for system evolution is derived by utilizing the square overlaps between the eigenstates of the Hamiltonian and the basis states， and employing degenerate perturbation theory. Ultimately， by assigning weights to the graph's edges， the stages of the quantum search are merged， thereby shortening the system evolution time and manifesting a quadratic speedup. This exploration elucidates the impact of weighted edges on the quantum search process.

Keywords： quantum computation; quantum search; continuous-time quantum walk algorithm; structured database

0  引  言

自从Feynman在1981年提出量子计算的概念以来，量子游走算法一直被认為是实现量子计算的一个关键组成部分。特别是当Grover量子搜索算法在结构型数据库中表现出的局限性，使其不能实现二次加速的最佳效果时，量子游走算法成为提高量子搜索效率的潜力算法[1，2]。

量子游走，又称量子随机行走算法，是经典随机行走的量子版本。量子随机行走算法分为离散时间量子行走和连续时间量子行走[3]。其中连续时间量子行走的思路来源于经典的连续型马尔可夫过程，所以常借助于图来进行描述，所以也更适合求解能够表示成结构图的问题，在量子领域中包括搜索、模拟、优化和图论问题。在量子搜索的问题上，可以代替Grover算法在结构型数据库中实现二次加速的搜索效果[4，5]。

本论文的目的是研究连续时间量子行走算法在截断单行晶格中，解决量子搜索问题的应用。我们讨论了阶截断单形晶格的结构特点，然后运用连续时间量子行走算法实现量子搜索.这一过程包括分析对晶格结构进行对称性分析，并讨论了寻找系统演化需要的临界跳跃率的两种方法。最后，我们通过对晶格上特定的边进行加权对量子搜索的影响，并压缩系统演化的时间，实现平方加速效果。

1  连续时间量子行走算法在截断单形晶格中的应用

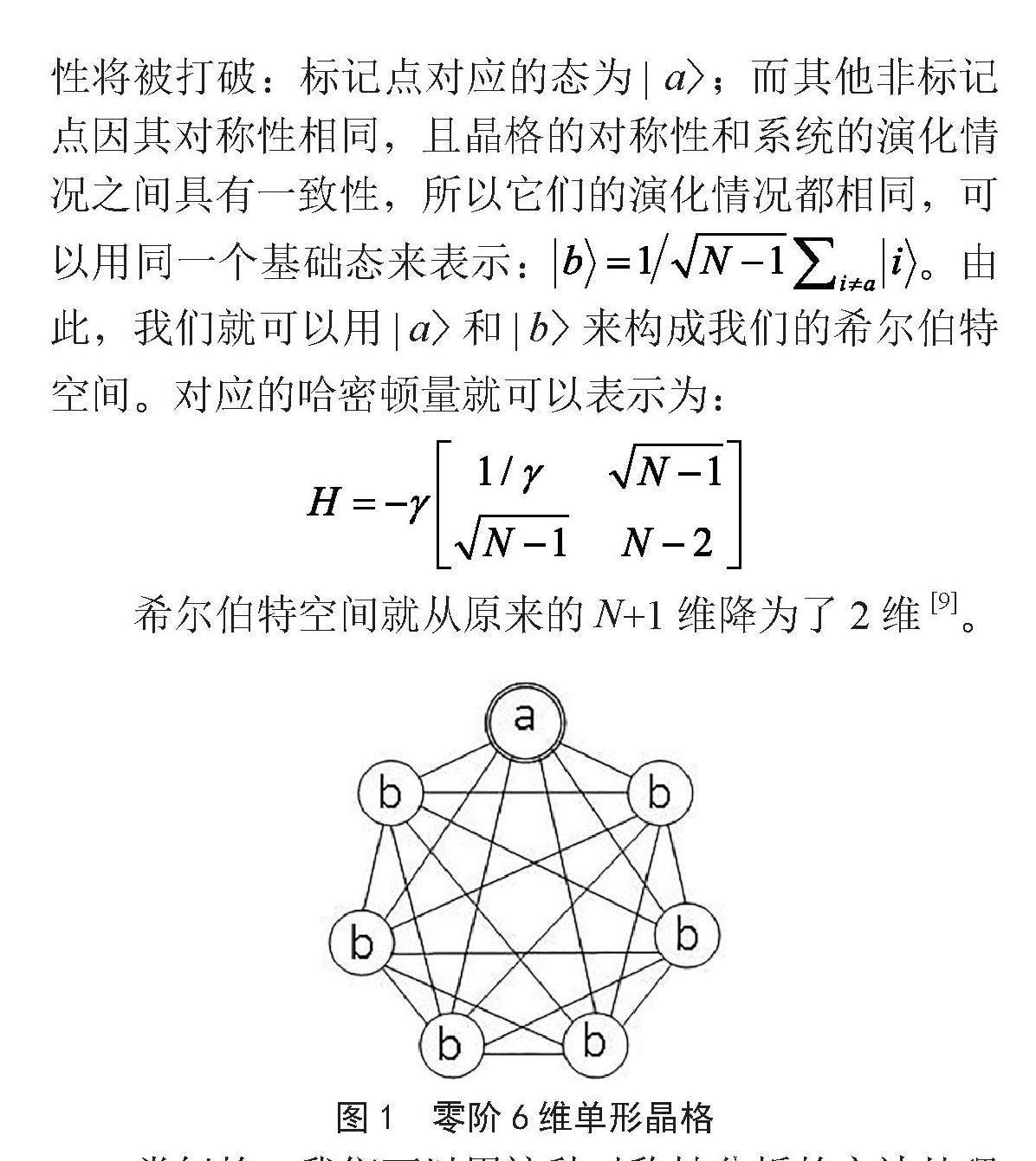
截断单形晶格因其具有有效的非整维数而得到了广泛的关注[6]。一个零阶截断M维单形晶格是指一个由（M+1）个结点构成的完全图，如图1是一个零阶6维单形晶格，其中用双线圈围成的点是目标态| a〉。单线圈围成的点为演化相同的点，表示| b〉。当该完全图上的各点均被一个M维完全图取代时，就可以得到一个一阶截断M维单形晶格，如图2是一个一阶6维单形晶格。以此类推，一个r阶截断M维单形晶格是由一个（r-1）阶晶格上的各点由M维完全图取代得来。其中双线圈围成的点为标记点a，其余点，根据对称性分析，演化情况相同的用相同的字母表示。

在量子系统中，信息用量子态表示。当结构型数据库用图表示时，图中的结点表示系统的各量子态，即对应不同的信息。当数据库用截断单形晶格表示时，系统演化需要的哈密顿量可以用图的拉普拉斯算子表示H = -γL，其中L = A - D。γ表示单位时间内，系统在邻接点之间进行演化的概率振幅，被称为跳跃率；A表示图的邻接矩阵；D表示以各点度数为对角元的对角矩阵。

因为截断单形晶格是正则图，即每个顶点都有相同的度数。在哈密顿量H的表达式中，D成为单位矩阵的整数倍。当省略D时，对搜索的效果并没有影响。所以哈密顿量H中的拉普拉斯算符L可以用图的邻接矩阵A替代，即H = -γA。并且，在正则图上使用连续时间量子行走算法时，用邻接矩阵A或拉普拉斯算子L构造哈密顿量H，对实验的结果并没有影响[7]。

其次，为了表示我们需要搜索的目标态，我们将其在图上对应的结点设置为标记点，如图1中的点a。为了使系统演化到目标态，我们需要在哈密顿量H中引入一个oracle项，此时哈密顿量H可以表示为 [8]。

连续时间量子行走相较于离散时间量子行走，不需要硬币空间，也不需要抛硬币，但是需要找到一个合适的γ值，即临界跳跃率γc，使系统可以从所处的初始状态朝目标态的方向进行演化。接下来，我们将具体讨论临界跳跃率γc的求解过程。

1.1  结构型数据库的结构分析

对于如图1所示的零阶截断N维单形晶格，即一个拥有（N+1）个结点的完全图，我们可以将该系统对应的哈密顿量H表示为：

相应的，系统演化所处的希尔伯特空间是N+1维。

但是当系统较为复杂，N的数目较大时，处理N维矩阵就显得较为困难。为此，我们需要对希尔伯特空间进行降维。设我们的目标态为| a〉，如图1中的点a为我们目标态对应的标记点。此时图1中的对称性将被打破：标记点对应的态为| a〉；而其他非标记点因其对称性相同，且晶格的对称性和系统的演化情况之间具有一致性，所以它们的演化情况都相同，可以用同一个基础态来表示：。由此，我们就可以用| a〉 和| b〉 来构成我们的希尔伯特空间。对应的哈密顿量就可以表示为：

希尔伯特空间就从原来的N+1维降为了2维[9]。

图1  零阶6维单形晶格

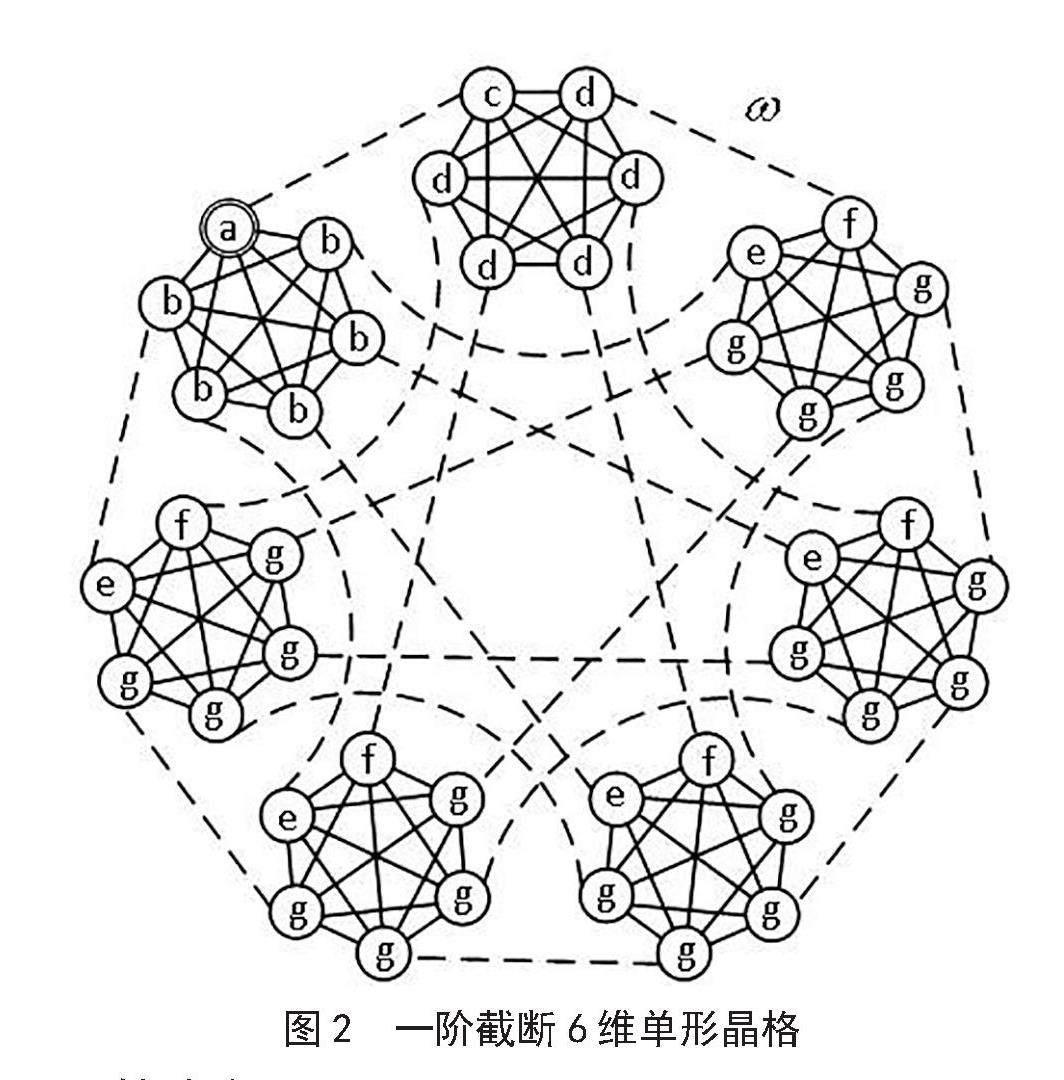
类似的，我们可以用这种对称性分析的方法处理更复杂的图，如图2的一阶截断6维单形晶格。该图共有42个点。但是当我们引入标记点a，然后根据对称性分析，我们可以将系统演化的希尔伯特空间降至7维，由{ | a〉 ，| b〉 ，| c〉 ，| d 〉 ，| e〉 ，| f 〉 ，| g〉 }组成。且分析证明，即使该一阶截断单形晶格的维数M增大时，这个7维不变子空间仍然适用。且这种对称性分析的方法适用于其他正则图结构如超立方体图，和非正则图结构如树[10，11]。

图2  一阶截断6维单形晶格

1.2  算法应用

当在结构型数据库中进行搜索时，因为不知道和目标态有关的信息，所以我们选择一个初态，使系统的概率是平均分配到图上的每个点，即每个点或每个状态都有可能是我们的目标。该初态也是物理实验中较常采用和较易制备的，可以表示为 。如图1的完全图中，标记点用a表示，非标记点用b表示。系统哈密顿量可以表示为H = -γA - | a〉 〈a |。当结点数目很多时候，b点的数目N - 1≈N，所以初态| s〉 ≈| b〉。

我们解跳跃率γ取不同值时，哈密顿量H的本征值和本征态，并求本征态与基础态的平方叠加，H = 100维的完全图上如图3所示。从图中我们可以看出，当Nγ = 1，亦即γ = 1 / N时，H的本征态为 ，且两本征态之间的能量差值最小为 。这里，γc = 1 / N即完成搜索需要的临界跳跃率。此时，初态和系统的状态可以表示为  和

，系统状态

会随着时间的推移而在  和  之间进行周期性振动，

对应概率可以表示为 和 ，其中?E10 = E1 - E0。令

|〈a | Ψ （t）〉 | 2 = 1，得t = π / ?E10。所以，当γ = 1 / N时，经t = π / ?E10后，系统可以从| s〉  演化到| a〉，搜索完成[5]。

图3  哈密顿量H的本征态和基础态之间的平方叠加

除了上述取多個γ值，然后求哈密顿量本征态和基础态之间平方叠加的方法外，我们还可以将简并微扰理论应用到连续时间量子行走算法中，来求解临界跳跃率γc和系统演化的时间t [10]。仍以图1的完全图为例，我们根据简并微扰理论，将哈密顿量H拆分为H = H （0） + H （1）。其中  是领先项， 是微扰项。领先项H （0）的本征态即| a〉 和| b〉 ，对应的本征值，即对应的能量为-1和-γN。当使两本征态对应能量相等时，γ = γc = 1 / N，再引入微扰项H （1），系统的本征态可以用αa | a〉 + αb | b〉 表示。以{ | a〉，| b〉 }为计算基，将哈密顿量H重新展开，得本征态和本征值为  和 。同样的，取时间 ，系统可以从| b〉 演化到| a〉。因为当完全图的点足够多时，| s〉 ≈| b〉 。所以当γ = 1 / N时，经 ，系统可从初态| s〉 演化到目标态| a〉 。

当晶格阶数增加，从零阶增至一阶时，系统的搜索需要两步来完成。并且每一步需要的临界跳跃率γc将有所不同。在使用简并微扰理论进行求解时，也将需要对哈密顿量进行不同的拆分，且每一步选择的领先项也将有所不同。特别是阶数升至二阶甚至更高阶时，领先项的选择将需要明显参照系统演化发生的局部结构。总结规律得，设截断单型晶格的阶数为r，则搜索需要的步骤为步，对应的临界跳跃率分别为γc1 = （r + 1） / M，γc2 = r / M，…，1 / M，所需时间为t ∝ M （2r + 1） / 2，M （2r + 1） / 2，…，M 1 / 2，即t ∝ N （2r + 1） / （2r + 2），N （2r - 1） / （2r + 2），…，N 1 / （2r + 2）。其中M为截断单形晶格的维数，N是晶格所有结点的数量N = （M + 1） M r。当阶数增加时，系统演化需要的时间也将增加，不能实现平方加速。我们可以通过增加图中边的权重，来缩短时间，我们在下一节中进行讨论[11，12]。

除了截断单形晶格以外，其他图如超立方体图、树、d维拉丁图和Johnson图等也实现了用连续时间行走算法完成量子搜索[5，13-17]。连续时间量子行走算法的使用中，解哈密顿量H本征态和基础态平方叠加的方法寻找临界跳跃率γc应用较为广泛，而簡并微扰理论目前只在截断单形晶格和超立方体图上得以成功运用[10]。

2  实现平方加速

在截断单形晶格上使用连续时间量子行走算法时，若晶格阶数超过0时，系统演化将不能实现时间上的平方加速效果。如图2的一阶截断6维晶格上，系统从初态  演化到目标态| a〉，需要两个步骤| s〉 → | b〉 → | a〉。两个步骤对应的临界跳跃率为γc1 = 2 / M和γc2 = 1 / M，对应的时间为t1 =

πM 3/2 / 4和t2 = πM 1/2 / 2。整个搜索过程系统演化需要的时间为t = t1 + t2 = πM 3/2 / 4 + πM 1/2 / 2 = Θ （M 3/2） = Θ（N3/4）。可见，此时的量子搜索不能达到平方加速的效果。

为了缩短量子搜索的时间，我们首先将一阶截断M维单形晶格看成是M + 1个“零阶截断单形晶格”彼此连接构成。我们称这M + 1个“零阶截断单形晶格”为“零阶完全子图”。一阶截断单形晶格上的两步演化中，第一步演化需要的时间较长，并且是造成量子搜索不能达到平方加速效果的原因。而第一步从| s〉 ≈| g〉 演化到 | b〉 的过程，可以看成是两个零阶完全子图之间的演化。然后我们选择在零阶完全子图之间的边上增加权值，即在图2所示的虚线上增加权重ω。

用简并微扰理论求解系统演化第一步的临界跳跃率为γc1 = （1 + 1 / ω） / M，此时演化所需的时间为t1 = πM 3/2 / [2 （1 + ω）]。而第二步的演化是 | b〉 → | a〉，在图2中是同一个零阶完全子图中不同点之间的演化，所以不受权值为ω边的影响，所以系统演化的总时间为t′ = t1′+t2 = πM 3/2 / [2 （1 + ω）] + πM 1/2 / 2。当ω = 1时，γc1 = 2 / M，且系统演化的时间为t1 = πM 3/2 / 4。但是我们增加ω的取值时，t1就可以减小。当我们取  时，就可以使 ，从而实现平方加速的效果[18]。

但是这样的加速需要以降低系统演化成功的概率为代价。当  时，虽然系统演化的时间被缩短了，但是 | s〉 → | b〉 〉演化成功的概率从不加权时的接近100%降低到了30%左右。而其余70%左右的概率分别以40%左右的概率演化到了 | a〉 和30%左右的概率停留在了 | s〉。当我们继续增加ω到M时，取γc1 = 2 / 3M + 2 / M 2，系统经时间t = πM / 1.83，以更高的概率演化到了 | a〉，而演化到 | b〉 的概率几乎为0。如图4所示，Pa表示系统演化到 | a〉 的概率，而Pb表示系统演化到 | b〉 的概率。此时，系统已经从 | s〉 → | b〉 → | a〉 的两步搜索合并成了 | s〉 → | a〉 的一步搜索，且时间 ，实现了平方加速的效果[12]。

图4  一阶截断单形晶格上系统演化的变化情况

3  结  论

连续时间量子行走算法是基于经典马尔可夫过程，对经典游走的量子模拟算法。因其更适合解决图表示的问题，所以相比较于Grover算法，更适合解决在结构型数据库上实现平方加速搜索的问题。

本文讨论了通过对称性分析对结构型数据库的结构进行分析，实现了系统演化所处希尔伯特空间的降维，并提供了确定临界跳跃率γc的两种方法，进一步求得系统演化所需的时间，使系统能够以较高概率演化到目标状态。最后我们讨论了给图上的边增加权重对量子搜索的影响，并通过加权压缩了系统演化的步骤，缩短了系统演化的时间，实现了平方加速。

虽然连续时间量子行走这一算法不是适用于所有搜索问题的通用解决方案，但它为解决一系列结构型数据库上的搜索问题提供了一种新的思路。至于进一步探索其他确定临界跳跃率γc的更简便方法，以及连续时间量子行走算法在搜索问题上、或其他领域中的应用等问题，对该算法的未来研究发展和进一步拓展探究都具有重要作用。

参考文献：

[1] GROVER K L. Quantum Mechanics Helps in Searching for a Needle in a Haystack [C]//Quantum Entanglement and Quantum Information--Proceedings of CCAST （World Laboratory） Workshop.Beijing：中国高等科学技术中心，1999：100-103.

[2] GROVER L K .Quantum Computers Can Search Arbitrarily Large Databases by a Single Query [J].Physical Review Letters，1997，79（23）：4709-4712.

[3] 薛鹏，王坤坤.量子行走 [J].光学学报，2024，44（2）：9-17.

[4] FARHI E，GUTMANN S .Quantum Computation and Decision Trees [J].Phys.rev.a，1997，58（2）：915-928.

[5] APERS S，CHAKRABORTY S，NOVO L，et al. Quadratic speedup for spatial search by continuous-time quantum walk [J/OL].Physical Review A，2021，95（3）：（2017-05-02）.https：//link.aps.org/doi/10.1103/PhysRevA.95.032301.

[6] DHAR D. Erratum：Lattices of effectively nonintegral dimensionality [J].J. Math. Phys.1977，18（12）：2520-2520.

[7] WONG T G，TARRATACA，LU?S TARRATACA，NAHIMOV N. Laplacian versus Adjacency Matrix in Quantum Walk Search [J]. Quantum Inf Process，2016，15：4029-4048.

[8] MOCHON C. Hamiltonian Oracles [J].Physical Review A，2007，75（4）：810-814.

[9] WANG Y，WU S. Role of symmetry in quantum search via continuous-time quantum walk [J/OL].SPIN，2021，11 （3）：2140002.https：//doi.org/10.1142/S2010324721400026.

[10] WONG，THOMAS G. Diagrammatic approach to quantum search [J].Quantum Information Processing，2015，14（6）：1767-1775.

[11] WANG Y，WU S，WANG W. Controlled quantum search on structured databases [J/OL].arXiv：2106.08398 [quant-ph].（2021-06-15）.https：//arxiv.org/abs/2106.08398.

[12] CHILDS A M. Optimal Quantum Adversary Lower Bounds for Ordered Search [C]//ICALP '08：Proceedings of the 35th international colloquium on Automata，Languages and Programming.Heidelberg：Springer-Verlag，2008：869–880.

[13] JANMARK J，MEYER D A，WONG T G .Global Symmetry is Unnecessary for Fast Quantum Search [J/OL].Physical Review Letters，2014，112（21）：210502（2014-05-28）.https：//link.aps.org/doi/10.1103/PhysRevLett.112.210502.

[14] MEYER D A，WONG T G. Connectivity is a poor indicator of fast quantum search [J/OL].Physical Review Letters，2015，114（11）：110503（2015-05-18）. https：//link.aps.org/doi/10.1103/PhysRevLett.114.110503

[15] CHAKRABORTY S，NOVO L，AMBAINIS A，et al. Spatial search by quantum walk is optimal for almost all graphs [J/OL].Physical Review Letters，2016，116（10）：100501 （2016-05-11）.https：//link.aps.org/doi/10.1103/PhysRevLett.116.100501.

[16] TANAKA H，SABRI M，PORTUGAL R. Spatial search on Johnson graphs by continuous-time quantum walk [J/OL].Quantum Information Processing，2022，21：74（2022-01-28）.https：//doi.org/10.1007/s11128-022-03417-9.

[17] APERS S，CHAKRABORTY S，NOVO L，et al. Quadratic speedup for spatial search by continuous-time quantum walk [J/OL].arXiv：2112.12746 [quant-ph].（2021-12-23）.https：//arxiv.org/abs/2112.12746.

[18] WONG，THOMAS G .Faster Quantum Walk Search on a Weighted Graph[J/OL].Physical Review A，2015，92（3）：032320 （2015-09-21）.https：//link.aps.org/doi/10.1103/PhysRevA.92.032320.

作者簡介：朱轩民（1983—）男，汉族，河南周口人，副教授，博士，研究方向：量子计算与量子信息；张德政（1998—），男，汉族，河北石家庄人，硕士在读，研究方向：量子计算与量子信息。