基于EKF的星地协同测向时差定位算法
王哲
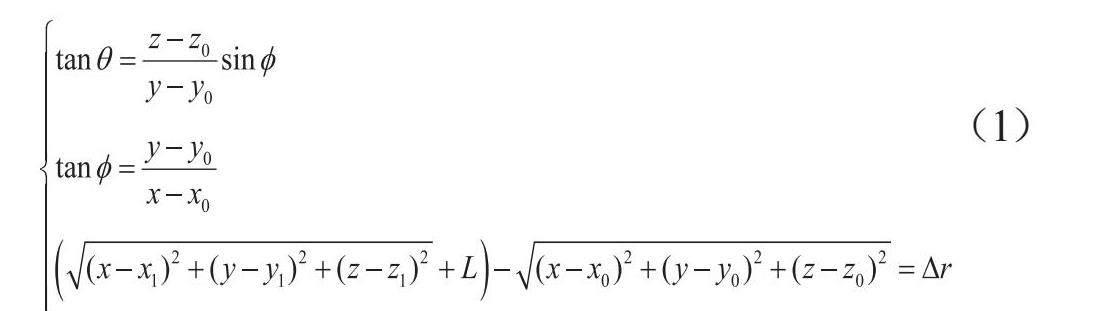

摘要:针对无源定位协同化需求,文章提出一种利用到达角、到达时间差的星地协同定位方法,分别研究其定位原理,建立数学定位模型,给出解算方法以及定位精度的表达式,推导基于测向时差参数的扩展卡尔曼滤波(EKF)算法。仿真结果表明该方法能够达到较高的定位精度;此外,该定位模型仅需单星,避免了传统星载平台定位需要寻找匹配邻星的问题,与机动平台配合,可对辐射源进行快速高效定位,具备一定的工程应用价值。
关键词:无源定位;星地协同;测向时差;扩展卡尔曼滤波
doi:10.3969/J.ISSN.1672-7274.2024.04.002
中图分类号:TN 96,TP 18 文献标志码:A 文章编码:1672-7274(2024)04-00-04
Satellite-ground Integrated DOA TDOA Location Algorithm Based on EKF
WANG Zhe
(The 54th Research Institute of CETC, Shijiazhuang 050081, China)
Abstract: Aiming at the integrated requirement of passive location, a satellite-ground integrated location method using direction of arrival (DOA) and time difference of arrival (TDOA) is proposed. Locating principle is studied, locating mathematical model is established, the solving method and the expression of location accuracy are given, and the extended Kalman Filter (EKF) algorithm based on DOA and TDOA parameter is derived, respectively. The simulation results show that this method can get higher location accuracy; In addition, this locating model only needs single satellite, and the problem of finding matching adjacent-satellite in traditional spaceborne platform location is avoided. With the cooperation of mobile platform, it can get fast and efficient location result of the radiation source. This method has certain engineering application value.
Keywords: passive location; satellite-ground integrated; DOA TDOA; EKF
0 引言
無源定位是辐射源信息获取中重要的一方面[1-3]。常用的定位方法适用于不同的平台数量,但通常平台样式较为单一,容易受到影响,目前缺乏有效的跨平台协同定位方法。地球同步轨道(GEO)卫星与地球相对静止,对地观测范围大,能够全天时、全天候工作,具有较强的信号接收能力,并能够对信号进行透明转发。将其与常规机动平台相结合,能够对辐射源进行高效定位。
本文在测向时差定位算法基础上[4-6],利用GEO卫星和机动平台相互配合,提出星地协同测向时差定位算法。传统双星或三星平台定位中需要主邻星波束同时覆盖目标,该算法避免了寻找匹配邻星的问题,且无需高程辅助信息就能对目标进行三维定位[7-10]。
1 算法原理
1.1 定位模型
星地协同测向时差定位系统由一个侦收主站和一个GEO卫星构成。一方面,主站可测得辐射源到主站的方位角和俯仰角;另一方面,主站分别接收辐射源直达信号和经卫星透明转发的信号,并计算得到时间差,由此可计算出距离差。从几何意义上说,求解空间目标位置的过程即是求解3个曲面(由确定的射平面、由确定的圆锥面以及由确定的双曲面)交点的过程。
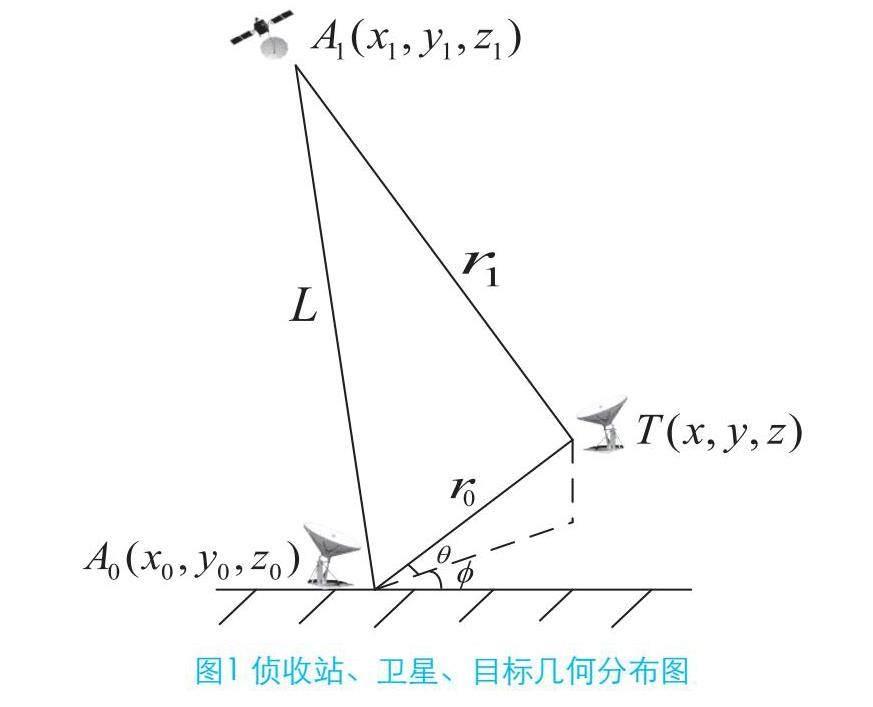
假设主站、GEO卫星的空间位置分别为:、,目标的空间位置为。目标到主站和GEO卫星的基线长度分别为(),GEO卫星到主站的距离为。几何关系如图1所示。
根据以上观测量,可以得到一个三元二次方程组:
(1)
式中,,为光速,。
1.2 算法求解
对式(1)进行变形整理,把看作已知量,建立线性方程组[11]:
(2)
式中,,,,。
在选择合适站址及卫星的条件下,为满秩矩阵,即,此时。用矩阵代替,得到:
(3)
由此解得:
(4)
辐射源位置与未知量有关,带入可解得,将其代入式得到目标的位置值。
2 定位精度分析
对式(1)各式变形、求微分得到定位误差方程:
(5)
式中,
将式(5)表示成矩阵形式:
(6)
式中,;;,
由式(6)整理之后得到:
(7)
相应的误差协方差矩阵为:
(8)
式中,,同时可求得;为俯仰角误差标准差;为方位角误差标准差;为目标直达信号与转发信号距离之差的误差标准差。
由此,可以求得误差协方差矩阵以及观测量对应的定位误差分布(GDOP)值:
(9)
3 扩展卡尔曼滤波算法及其应用
在测向时差定位系统中,观测方程是非线性的,可以利用EKF进行滤波处理来进一步提高定位精度[12-15]。
根据定位原理可知,滤波的状态向量为目标位置,观测向量为辐射源角度和到达两站的距离差(等同于时差)。由此可建立如下滤波数学模型。
状态方程:
(10)
式中,为目标位置;对于固定目标,为单位阵;为噪声且;为噪声的方差阵。
观测方程:
(11)
式中,;为观测噪声且;为噪声的方差阵。
将在当前估计的预测值处展开,得到:
(12)
式中,为观测方程在预测值处的雅可比矩阵。
此时,将式(12)代入观测方程(11),整理为:
(13)
式中,。
得到线性化的观测方程后,EKF定位方法的滤波递推公式总结如下:
(14)
(15)
(16)
(17)
(18)
可以将定位算法解算得到的目标位置作为滤波初值,同时初始化协方差矩阵,根据时刻的观测值,可以递推求出目标的位置解。
4 算法仿真
对于该定位模型,给出单次定位仿真结果、EKF仿真结果。
按照下式计算相对定位误差:
(19)
仿真条件设置如下:主站坐标(113°E,30°N),海拔高度50 m;GEO卫星选择中卫1号(87.5°E);主站、卫星均为任意选取;目标坐标(111°E,34°N),海拔高度10 km;站址误差3 m,时差误差100 ns,方位角、俯仰角误差均为1°;卫星轨道误差设定为100 m;Monte-Carlo次数50次;EKF滤波步数200,间隔1 s。
由图2可以得到,200个点的单次定位结果散布在真实值四周,且误差较大的点数与距离呈正相关,符合预期。图3的仿真结果表明,单次定位的相对定位误差大约为2.4%,经过EKF处理后的相对定位误差80 s后收敛到1%左右,最终收敛到0.7%左右,EKF有效提升了定位精度。
5 结束语
本文在双站测向时差定位算法的基础上,结合当前对于无源定位网络化、协同化的需求,提出星地协同测向时差定位算法,介绍了定位原理及解算方法,并推导出定位误差的表达式,对其进行仿真研究。针对慢速或固定目标,利用EKF对测量参数进行滤波,给出了该模型下的EKF递推公式。仿真结果表明,EKF收敛快、能够有效提高定位精度。■
参考文献
[1] 胡来招.无源定位[M].北京:国防工业出版社,2004.
[2] 孙仲康,周一宇,何黎星.单多基地有源无源定位技术[M].北京:国防工业出版社,1996.
[3] POISEL R A. Electronic Warfare Target Location Methods[M]. USA: Artech House, 2012.
[4] 陈玲,李少洪.无源测向测时差定位算法研究[J].电子与信息学报,2003,25(6):771-776.
[5] 刘建林.多站无源定位技术研究与应用[D].西安:西安电子科技大学,2011:25-35.
[6] 周国辉,刘湘伟.多舰协同侦察的无源测向时差定位方法[J].现代雷达,2011,33(10):23-27.
[7] 张艳.三星时差频差联合目标定位与跟踪算法研究[D].西安:西安电子科技大学,2014.
[8] 赵勇胜,赵拥军,赵闯.基于角度和时差的单站多外辐射源融合定位方法[J].信息工程大学学报,2016,17(2):675-680.
[9] 孙哲,霍立寰,柏如龙,等.基于多重广义Hough变换的多星时频差联合定位方法[J].无线电工程,2021,51(11):1284-1288.
[10] 钟丹星,邓新蒲,周一宇.一种基于WGS-84地球面模型的卫星测时差定位算法[J].宇航学报,2003,25(6):569-573.
[11] 任玥.基于各種辅助方法的无源定位体制及算法研究[D].成都:电子科技大学,2008.
[12] 何青益,李红伟.基于EKF的时差定位算法[J].舰船电子对抗,2013,36(3):79-81.
[13] 李美红,尹健,徐劲祥.基于EKF的机载光电吊舱目标定位研究[J].弹箭与制导学报,2016,36(6):157-161.
[14] 李炳荣,丁善荣,马强.扩展卡尔曼滤波在无源定位中的应用研究[J].中国电子科学研究院学报,2011,6(6):622-625.
[15] 李仕云.基于EKF的双站测向/时差联合定位算法[J].无线电通信技术,2015,41(1):38-40,93.

