一种游动傅科机械编排的捷联惯性间接极区导航算法

孙新雷，尹浩凌，富立，王玲玲

（1.北京航空航天大学机械与控制工程国家级（虚拟仿真）实验教学中心，北京 100191；2.莫斯科罗蒙诺索夫国立大学力学数学系，莫斯科 119991）

0 引言

极地地区在资源开采、科研探索、国家安全等方面都具有独特的地位［1-3］。因此，在空间和资源竞争日益激烈的国际形势下，各国逐鹿两极的态势早已形成，大量勘测队伍相继被派往极区开展地形测绘和资源勘探。极区飞行器在执行勘测、警戒、侦察、搜索和救援等任务时具备重要且独特的功能，其必要性和不可替代性显著。然而，由于极区的特殊的地理环境和极端气候条件，极区飞行器执行任务时面临着许多挑战。为了应对极区安全飞行的挑战，需要有高精度导航定位技术作为支撑。众所周知，极区附近存在经线收敛迅速、电磁干扰严重、太阳磁暴频发等现象，导致极区导航面临方向基准丢失、磁极位置漂移、无线通信受扰等困难。因此，目前的单一导航方式如卫星导航、磁罗经导航、天文导航和图像匹配等都难以直接用于极区导航［4-6］。

为了确保导航系统能够在极区附近长时间、高精度地工作，目前主要采用组合导航方法来弥补单一导航方式的不足。文献［7-8］研究了基于偏振光辅助的组合导航方法，其中偏振光导航可用于提供航向和姿态信息。在文献［9］中，提出了一种基于多普勒测速仪辅助的组合导航方法。该方法利用多普勒测速信息来校正惯性导航系统的方位角，从而提高其在极区的导航精度。文献［10-11］研究了卫星/惯性组合导航在极区的工作性能，文中利用卫星导航系统提供的位置信息校正惯性导航误差。可见，无论上述哪种方式，都是以惯性导航为中心开展的组合导航。这是因为惯性导航系统具有自主性好、环境适用性高、抗干扰能力强等优点，且能够为运载体提供姿态角、速度以及位置等自主导航信息，是目前最适用于极区附近的导航方式［12］。因此，提高惯性导航系统的精度是保证高精度极区导航的关键所在。

已有研究表明，惯性导航系统中常用的指北、游移方位等机械编排方式在极点附近存在计算溢出和导航误差发散等问题［13-14］。为了解决这些问题，学者们提出了地心地固（Earth-centred earth-fixed，ECEF）机械力学编排作为一种有效的解决方案［15-16］。该方法将地球坐标系作为导航坐标系，且所有的导航信息都基于该坐标系定义。当需要获取横滚、俯仰和偏航角信息时，可利用局部位置信息间接得到机体坐标系与地理坐标系之间的姿态角。然而，在两极地区，由于ECEF 坐标系的z轴与地理坐标系平行，偏航角将不再是唯一确定的。网格惯导机械力学编排和横向惯导机械力学编排也是常用的极区导航方法［17-20］。它们通过引入网格基准线和横向坐标系重新定义方向基准，避免了极区附近北向方向基准不可用的问题。然而，这两种方法间断式的导航坐标系切换对于平台惯导系统来说是无法实现的，只能用于捷联惯性导航系统。此外，导航坐标系切换过程中的计算误差可能导致导航解算精度下降。为了避免导航坐标系间的切换，一些学者设计并提出了基于伪地球坐标系和凝固地理坐标系的极区惯性导航方法［21-22］，实现了导航算法在全局区域的内在统一性和导航坐标系间的平滑切换。然而，上述文献中的伪地球坐标系和凝固地理坐标系的定义高度依赖于经度和纬度信息，因此位置误差会对导航系统的精度产生很大影响。近年来还出现了基于地球坐标系的法向量惯性导航力学编排方法［23］，该方法用法向量代替经纬度来进行位置更新，可适用于全球范围。然而，地球曲率半径的变化会对法向量惯性导航方法的计算精度产生不利影响。

综上所述，极区导航需要一种能够平滑转换坐标系、稳定且简单直观的机械编排方式。游动傅科机械力学编排方式为上述问题提供了一种全新的解决方案［24］。该编排方式既适用于平台和捷联惯性导航系统，又能够实现导航误差的部分解耦。在此基础上，本文首先推导并验证了基于游动傅科机械力学编排方式的捷联惯性导航算法。其次，通过引入横向导航信息进行间接导航解算，成功解决了游动傅科机械力学编排方式在极点处导航信息无法分离的问题，使得基于游动傅科机械力学编排的惯性导航系统能够在全区域（包括极区附近）正常工作。

1 游动傅科机械力学编排的捷联惯性导航算法

1.1 坐标系定义

本文涉及到的坐标系定义如图1所示。其中用下标简称各坐标系：e为地心地固坐标系，b为载体坐标系，g为地理坐标系，eˉ为横向地心地固坐标系，gˉ为横向地理坐标系，其具体定义可以参考文献［25］。

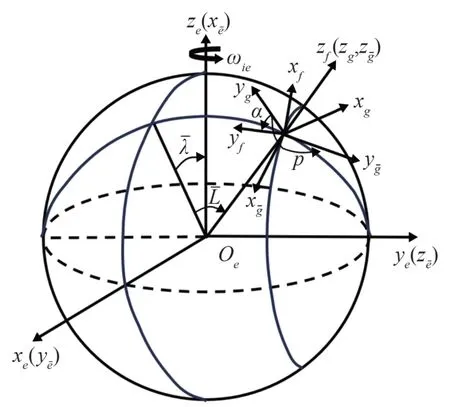
图1 惯性导航相关坐标系Fig.1 Inertial navigation related coordinate systems

f为局部水平游动傅科坐标系［24］（简称傅科坐标系）。游动傅科坐标系以载体所在的真实地理位置为原点，y轴初始时指向北极，z轴沿局部重力矢量方向，构成右手标准正交坐标系。游动傅科坐标系相对惯性坐标系在z轴上的旋转分量为零（即=0）。此外，游动傅科坐标系与游移方位坐标系［13］有许多相似之处，二者均为局部水平坐标系，且z轴始终与局部重力矢量方向保持平行，并指向向上的方向。游动傅科坐标系与游移方位坐标系的区别在于傅科坐标系的z轴无地球自转分量（该分量即为傅科振荡）。因此，游动傅科坐标系相对游移方位坐标系以(360°/24 h) · sin(L)的角速度旋转。

1.2 游动傅科坐标系下惯性导航方程

基于以上游动傅科坐标系的定义，容易得到游动傅科机械力学编排的导航方程

式中：f b为加速度计比力测量矢量在载体坐标系下的投影为载体对地速度矢量在傅科坐标系中的投影为重力加速度矢量和为牵连角速度矢量；符号(·)×表示反对称矩阵运算。一般地，对于三维矢量a=[a1a2a3]T，可定义(a)×为：

式中：α为游动角，即游动傅科坐标系y轴与北向之间的夹角为载体坐标系到地理坐标系的方向余弦矩阵。此外，游动傅科机械编排方式的位置矩阵与游移方位机械编排具有类似的形式［26］。式（1）中的牵连角速度可由载体对地速度在游动傅科坐标系中的投影求得：

1.3 游动傅科机械编排惯性导航误差分析

忽略二阶小量的影响，游动傅科坐标系下的姿态误差方程可以表示为

式中：φf表示计算得到的傅科坐标系与理想傅科坐标系之间的偏差角，即平台误差角+表示傅科坐标系相对惯性坐标系的角速度；εf为陀螺在傅科坐标系内的等效漂移。根据式（5）可以得到平台误差角沿傅科坐标系x，y，z轴分量的具体形式：

式中：ωie为地球自转角速度，δv为速度误差，δα为游动角误差，δh为高度误差，δλ和δL分别为经度和纬度误差。

游动傅科坐标系下的速度误差满足如下方程：

式中：f f表示比力在傅科坐标系中的投影，∇f为加速度计的等效偏置误差。根据式（8）可以得到速度误差沿傅科坐标系x，y，z轴分量的具体形式：

进一步，可以得到位置误差方程：

式中：vE和vN分别表示东向对地速度和北向对地速度，可以由式（14）计算得到：

航向角误差为：

式中：φz为平台误差角沿傅科坐标系z轴的分量，δα为游动角误差。

1.4 游动傅科机械编排惯性导航误差特性

在常用的地理导航坐标系下，导航误差模型可以被近似为耦合的非线性时变系统。但航向误差中存在纬度的正切项，当载体接近极点时，该正切项将趋于无穷大，从而导致航向角误差指数级增长，呈现发散状态。另一方面，在地理导航坐标系中，载体航向角与纬度之间存在的非线性关系会随着载体位置的变化而改变，也会增大航向角误差。为解决以上问题，最直接的方法就是采用游移方位坐标系作为导航坐标系，以便消除航向角误差方程中的正切项。此时，相对于导航坐标系而言，姿态角误差的微分不会发散［28］。然而，纬度的增加仍然会降低导航误差的估计精度，这种影响从游移方位坐标系转换到地理坐标系的代数运算过程中，即它被转移至游动角误差中。也就是说，引入游移方位坐标系仍无法解决导航误差高度耦合的问题。鉴于游动傅科坐标系的特殊定义，其具备将导航误差的水平分量在惯性坐标系和傅科坐标系之间实现部分解耦的能力，即解耦水平通道位置误差。为了更加便捷地分析和表示位置、速度和加速度误差之间的关系，考虑以下形式的导航误差方程：

式中：qf为载体在游动傅科坐标系中的位置，Δqf为位置误差是惯性坐标系到傅科坐标系的正交变换矩阵。根据游动傅科坐标系的定义易知，游动傅科坐标系相对惯性坐标系的角速度为：

式中：vf为傅科坐标系下的惯性速度表示由地球曲率引起的傅科坐标系相对于惯性空间的旋转矢量，R是地球半径。由于在傅科坐标系z轴上的分量为零，使得式（16）所示的误差方程水平分量对于位置矢量的解耦成为可能。对式（16）进一步变形可得：

式中：Δf b表示比力测量误差，φf表示平台误差角（即实际傅科坐标系与理想傅科坐标系不重合引起的误差），ΔGf表示局部重力加速度估计误差。

由式（18）可以得到误差方程沿x轴和y轴分量的具体形式：

式中：舒勒反馈环节的特征频率ωs由载体受到的重力加速度和离心力共同决定。由式（20）可知，误差方程中的和之间实现了解耦，从而可以更好估计并补偿惯性导航系统的误差。由此可见，傅科坐标系在导航误差分析过程中具有优势。

2 极区导航算法

虽然游动傅科捷联惯性导航系统在高纬度地区有较好的工作性能，且具有水平误差分量可解耦的优点，但该系统在极点附近工作时仍然面临和游移方位导航系统同样的困境，即纬度L趋近于90°时有：

此时，位置矩阵可以简化为：

由式（22）可知，此时经度λ和游动角α无法分离，这将导致航向角计算失效［27］。为避免上述问题，本文采用横向导航信息来进行间接极区导航，从而拓宽游动傅科导航系统的适用范围。

2.1 传统导航信息与横向导航信息的转换

横向坐标系的提出最早是为了解决惯性导航系统在极区附近存在物理奇点的问题［28-29］。如图1所示，定义90°E经线与赤道线的交点为横向北极点，地理坐标系（g系）与横向地理坐标系（gˉ系）之间的夹角为p。分别记经度和纬度为λ和L，横向经度和纬度为和，地球半径为R，载体所在位置的水平高度为h。那么地球上任意一点P的位置可以表示为：

由式（23）可以得到传统位置信息与横向位置信息之间的转换关系：

此外，地理坐标系（g系）与横向地理坐标系系）之间的正交变换矩阵可以表示为：

式中：夹角p的值域为(-180°，180°]，可根据反正切和反余弦函数的值来确定。

2.2 游动傅科捷联惯性间接极区导航

游动傅科坐标系与地理坐标系和横向地理坐标系具有如图2 所示的角度关系。其中，α为传统游动角，β为横向游动角，p为地理坐标系与横向地理坐标系之间的夹角，Ng和Eg分别为地理北向和东向和分别为横向地理的北向和东向。

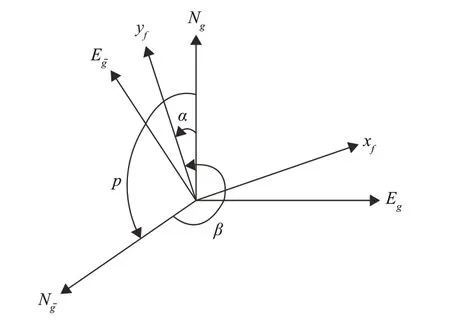
图2 傅科坐标系和地理坐标系Fig.2 Foucault coordinate and geographic coordinate

由图2可以看出传统游动角和横向游动角之间具有如下关系：

当载体进入极点附近区域时，仍采用游动傅科坐标系作为导航坐标系，但需要将导航信息解算到横向坐标系中再间接求出导航信息。设载体进入极点附近区域时的游动角为α0，地理坐标系与横向地理坐标系的夹角为p0，则初始横向游动角为

由于导航坐标系没有发生改变，基于横向导航方式的游动傅科机械编排惯性导航系统的导航方程仍然为式（1）。但需要将坐标变换矩阵和中各项元素替换成横向坐标系下的位置和姿态信息，即将式（1）和式（2）中的λ，L，α分别替换成，，β。由于地理坐标系与横向地理坐标系均为当地水平坐标系，则两种导航方式下姿态角之间的关系可以表示为：

式中：δψ为地理北向与横地理北向之间的夹角，可以下式计算得到：

在极点附近区域使用式（1）求解载体速度和位置时，需要注意的是地球自转角速度在横向地理坐标系中的投影为

2.3 游动傅科捷联惯性间接极区导航的实现

由2.2 节中的推导可知，当载体运动到极点附近区域时，仍然可以采用游动傅科机械编排方式，但需要将导航信息转换到横向坐标系中。此外，载体在该区域边界运动时，可能会出现频繁切换导航方式的情况，因此实际应用时应选取不同纬度L2和L1(L2＞L1)作为“进入”和“退出”捷联惯性间接极区导航方式的阈值。游动傅科捷联惯性间接极区导航算法的实现流程如图3所示。

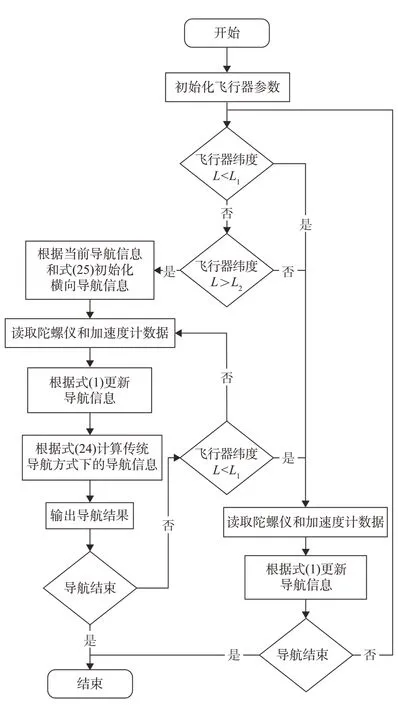
图3 极区导航算法流程图Fig.3 Flowchart of polar navigation algorithm

在游动傅科捷联惯性间接极区导航方法中，首先根据载体当前位置和游动角信息由式（30）计算出横向初始游动角β0，并通过式（25）将当前导航信息转换为横向导航信息。由于转换前后导航方程都是投影到游动傅科坐标系中，故转换前后不需要进行导航算法的改变。但需要注意，采用游动傅科捷联惯性间接极区导航方式时，傅科坐标系的牵连角速度是相对横向坐标系而言的。

3 仿真校验

3.1 游动傅科惯性导航系统误差分析

极区导航有两点需要注意：重力加速度矢量与地球自转角速度矢量几乎平行，经线快速收敛导致较小的位置变化可能引起很大的经度变化。正因如此，目前绝大多数机械力学编排方式都无法胜任极区导航工作［30］。为了验证游动傅科机械编排方式在高纬度地区的工作性能，采用一条沿经线飞行的轨迹进行导航误差仿真。

假设载体沿经线方向向北航行，在行驶过程中载体坐标系相对当地地理坐标系始终保持重合，即载体的姿态角不发生改变。具体仿真条件设置为：初始经度λ0=120°E，初始纬度L0=82°N；东向速度vE=5 m/s，北向速度vN=50 m/s，天向速度vU=0 m/s，飞行高度h=6 000 m，这是大多数长航时无人机较为合适的飞行速度和高度；初始姿态角为0°，初始游动角α0=0°。陀螺漂移误差εx=εy=εz=0.01°/h，加速度计偏置误差为∇x=∇y=∇z=5 × 10-5g，不考虑传感器的标度因数误差。仿真飞行总时长设置为3 h，结束时载体所在位置纬度为Lend=86.8°。

为了更清晰、更明确地分析游动傅科导航系统的误差特性，实验过程中将其与一些常用惯性导航系统的误差进行了对比。图4、图5、图6 分别示出了不同机械编排方式下的捷联惯性导航姿态误差、速度误差和位置误差。由此可见，采用游动傅科机械编排方式进行导航解算后，与指北方位机械编排方式和游移方位机械编排方式相比较，三者的俯仰角和滚转角误差、东向和北向速度误差、经度和纬度误差结果基本相同。这一性质称为误差模型的等价性，即不管惯性导航系统选择何种平台坐标系和导航解算坐标系，它们的系统误差模型变换到同一个坐标系中，都具有相同的方程、相同的自由振荡和相同的误差传播特性［31］。对于捷联惯性导航系统，以上三种不同机械编排导航方式的误差源和传播特性相同，因此表现出相同的位置、姿态和速度误差特性，仿真结果也验证了这一点。然而，由于三种机械编排方式下航向角的定义方式不同，航向角误差存在明显的差异，但这并不会影响到位置和速度误差的特性。

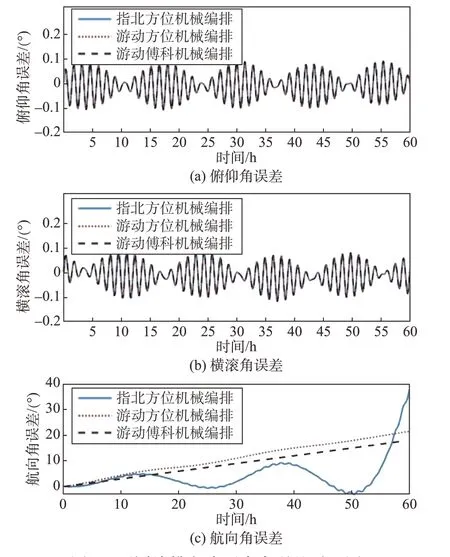
图4 不同编排方式下姿态误差对比图Fig.4 Comparison of attitude errors under different mechanization

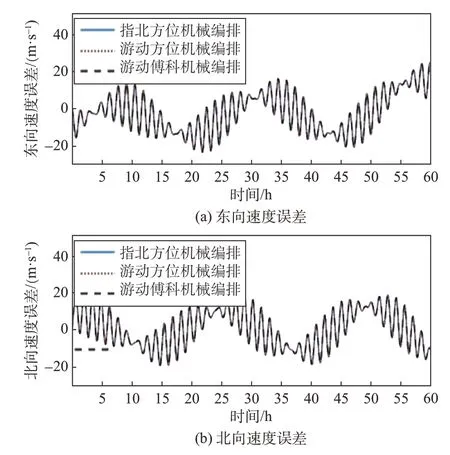
图5 不同编排方式下速度误差对比图Fig.5 Comparison of velocity errors under different mechanization

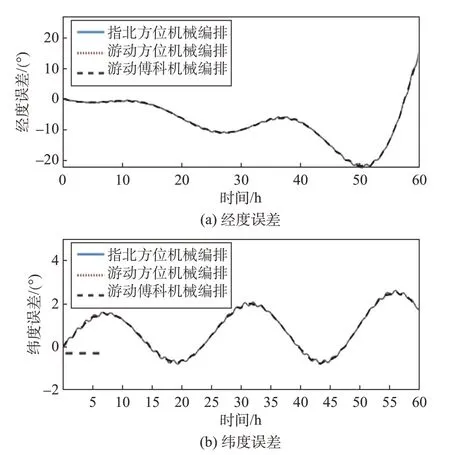
图6 不同编排方式下位置误差对比图Fig.6 Comparison of position errors under different mechanization

此外，由图4（c）和图6（a）容易看出，以上三种机械力学编排方式的航向角误差和经度误差都会随着纬度的升高逐渐发散。也就是说单纯的游动傅科机械力学编排方式仍然无法解决航向角误差和经度误差在极点附近发散的问题。

3.2 导航方式切换验证

本文提出的游动傅科间接极区惯性导航算法旨在确保惯性导航系统全局区域内的一致性，并实现不同导航方式的平滑切换。本节通过仿真示例对比并分析游动傅科捷联惯性间接极区导航方法、基于横向地理的惯性导航方法在导航方式切换时的情况。考虑到实际极区导航数据难以获取；纯数学仿真方法只能用于算法可行性的验证，但难以反映真实环境对于导航方式切换的影响；目前多数研究采用半物理模拟的方法生成极区导航数据。通常将惯性测量组件放置在三轴转台上，通过旋转转台模拟载体的角运动，通过数字输入比力模拟载体的线运动［32］。另一方面，考虑到极区导航数据的主要特征是地球自转角速度分量几乎与陀螺仪的天向轴重合，且较短时间内地球自转角速度的影响很小。因此，在短时间内可以忽略地球自转角速度的影响，用实验室内获得的陀螺数据模拟极区附近的载体角运动。按照上述半物理仿真方法，本文使用某高精度光纤陀螺惯性组件短时间内的静态实测数据（采样频率100 Hz）对导航方式切换过程中的导航性能进行分析。着重比较了游动傅科坐标系和横向地理坐标系作为导航坐标系时，捷联惯性导航系统在传统导航方式和横向导航方式切换时的姿态解算结果。具体对比结果如图7所示。

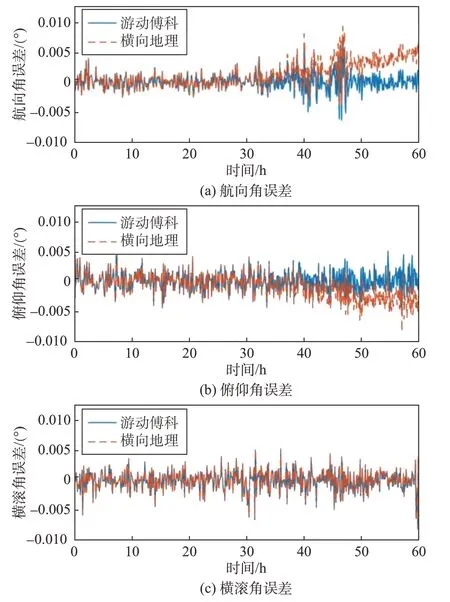
图7 导航方式切换时的姿态角误差对比图Fig.7 Comparison of attitude errors for navigation mode switching

本实验使用了时长为600 s 的实测数据来评估导航方式切换时的姿态解算结果。图7展示了游动傅科机械编排（方式1）和指北方位机械编排（方式2）两种不同的导航方式下的姿态解算误差。实线部分代表方式1，其全程采用游动傅科坐标系作为导航坐标系。在前300 s内，使用传统导航信息进行姿态解算；而在后300 s 改为使用横向导航信息进行姿态解算。虚线部分代表方式2，在前300 s 内采用地理坐标系作为导航坐标系，并使用传统导航信息进行姿态解算；而在后300 s，导航坐标系切换为横向地理坐标系，并利用横向导航信息进行姿态解算。

图7 结果表明，在前300 s内，两种方法的姿态解算误差基本相同，且均能以较高的精度实现姿态解算。然而，当切换到横向导航方式时，游动傅科惯性导航系统的性能几乎没有发生变化，其姿态解算误差仍然保持在接近0°的水平，而横向地理惯性导航系统的姿态解算结果则在300 s 内产生了0.005°的累积误差。造成这种情况的原因在于地理坐标系和横向地理坐标系之间的切换是不连续的，也就是说它们并不完全重合。这种不连续性导致重新计算姿态矩阵和位置矩阵时会引入误差，从而影响了姿态解算结果的准确性。本文提出的游动傅科间接极区惯性导航方法能够在不切换导航坐标系的情况下实现横向导航解算，避免了上述问题，说明该方法在导航方式切换时具有明显的优越性。

3.3 极地导航仿真验证

为验证本文提出的游动傅科捷联惯性间接极区导航算法在高纬地区，特别是载体通过极点地区的可行性，利用数值解的形式构造了一条沿经线穿过北极点的飞行轨迹，为所提出的极区间接导航算法进行实验验证提供仿真数据。

假设载体的航行轨迹为沿120°E经线向北航行，东向速度和天向速度设为vE=vU=0 m/s，北向速度设为vN=200 m/s，飞行高度h=10 km。航行时间为10 min，初始纬度为L0=89.5°，那么载体会在航行5 min 左右后穿越北极极点。航行过程中始终保持俯仰角、横滚角、航向角为00。当载体穿越北极点后将朝着远离极点的方向航行，此时经度λ将从120°E变为60°W，航向角ψ将从0°（靠近极点）变为180°（远离极点）。则游动傅科捷联惯性间接极区导航方法的姿态、速度和位置解算结果分别如图8、图9、图10所示。

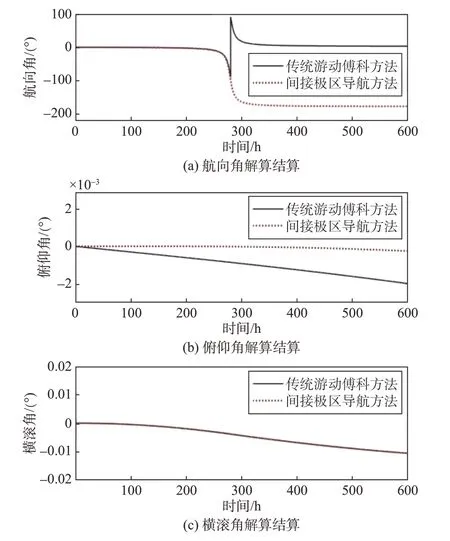
图8 游动傅科捷联惯性间接极区导航的姿态解算结果Fig.8 Attitude solving results of Foucault strapdown inertial indirect polar navigation

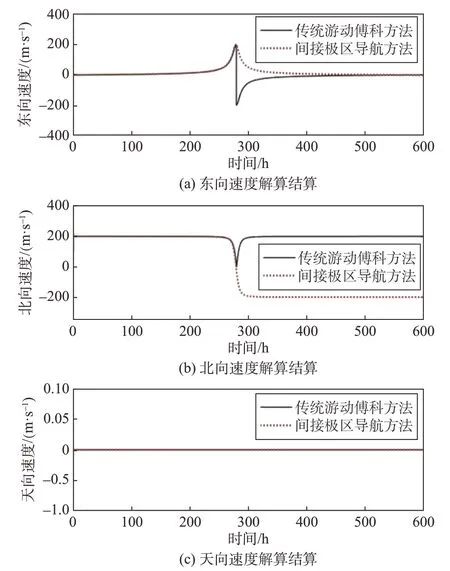
图9 游动傅科捷联惯性间接极区导航的速度解算结果Fig.9 Velocity solving results of Foucault strapdown inertial indirect polar navigation

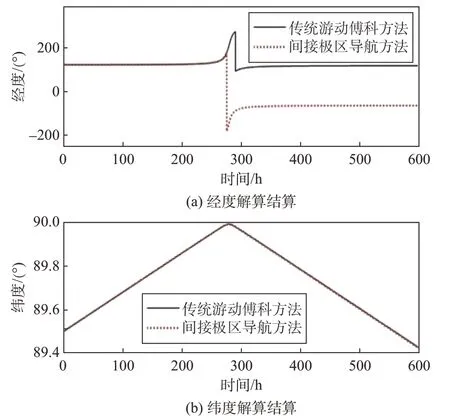
图10 游动傅科捷联惯性间接极区导航的位置解算结果Fig.10 Position solving results of Foucault strapdown inertial indirect polar navigation

由图8（a）和图10（a）可以看出，采用传统游动傅科捷联惯性导航算法进行导航解算时，载体穿越北极点前后航向角和经度的解算结果未发生改变（这与实际不符），也就是说传统游动傅科捷联惯性导航解算在穿越极点时失效。主要原因在于极点附近的位置矩阵退化，无法分离游动角和经度的值，进一步导致游动角和经度的符号无法确定，影响到航向角和经度的求解。此外，由图8、图9、图10可知，在不改变机械编排方式的前提下，借助横向导航信息进行导航解算，可间接求出正确的导航信息，并能够避免在极点处因L→90°出现位置矩阵退化的问题，从而解决了游动傅科机械力学编排方式在极点附近不适用的问题。可见，游动傅科捷联惯性间接极区导航算法能够满足载体高纬度飞行以及穿越极点飞行的导航需求。

由图8 可以看出，在上述传统游动傅科惯性导航方式和游动傅科惯性间接极区导航方式下，随着飞行时间的增加，俯仰角和滚转角的解算结果变化缓慢，而横滚角的变化明显大于俯仰角的变化（俯仰角误差的量级为10-3，横滚角误差的量级为10-2）。这是因为在捷联惯性导航解算过程中，计算精度和参数初始化误差会影响到数字平台计算的准确性，从而导致姿态解算误差。对于较短时间内的惯性导航解算，这样的误差是可以接受的。但对于长期的极区惯性导航，则需要GPS 等外部辅助信息对游动傅科坐标系进行重新对准，从而消除捷联惯性导航系统数字平台计算过程中的累积误差。

4 结论

为了解决传统惯性导航在极点附近出现的奇异性问题，本文首先分析了游动傅科机械编排惯性导航系统的误差特性。然而，分析表明该系统存在无法分离位置信息和航向角误差发散的缺陷。在此基础上，本文基于游动傅科坐标系和横向导航方法，设计了一种游动傅科捷联编排的间接极区导航算法。研究结果表明，该算法在载体接近极点时保持机械编排方式不变，可将导航信息映射到横向坐标系中，能够准确计算导航信息，并有效解决了纬度趋近于90°时位置矩阵元素无法分离的问题。由此可见，本文所提方法实现了传统导航方式和横向导航方式导航方程的统一，可为高纬度地区以及极点附近的安全航行提供高精度导航信息。