异构多星电磁编队静态构型设计与保持控制

蔡曜，杨盛庆，2，吴敬玉，2

（1.上海航天控制技术研究所，上海 201109；2.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

卫星编队因为可以在空间中组合成更大尺度的虚拟航天器，完成以往单颗卫星难以完成的任务，近年来成为航天领域的研究热点［1］。但基于动量原理的传统卫星编队需要消耗燃料实现相对位置保持，存在寿命受限、羽流污染等问题。针对这一问题，有研究［2］提出电磁编队飞行（Electromagnetic formation flight，EMFF）是一种可行的解决方案。电磁编队利用安装在卫星上的超导线圈，在星间产生电磁力实现编队的相对位姿控制。电磁编队仅消耗电能，具有更好的控制性能和更长的工作寿命，能够形成更丰富的编队构型，在空间任务中具有广阔的应用前景。

电磁编队动力学建模的基础是电磁力模型的选择。精确电磁力模型［3］基于毕奥-萨伐尔定律，需要对线圈的每个电流微元进行积分，没有解析解，只能采用数值方法求解。虽然模型精确，但计算复杂度较大，在构型设计与控制时直接使用存在计算量较大的问题。为了简化精确模型，Schweighart［4］假设线圈半径远小于线圈距离，对精确模型分别进行泰勒一阶和三阶展开，得到了电磁力远场模型和中场模型，并简要分析了线圈距离与半径之比对模型误差的影响。但该方法没有对模型误差与轨道摄动量级进行比较，忽略了模型误差对编队构型保持的影响。而且无论是哪个电磁力模型，电磁力、电磁力矩、磁矩和相对位置都是高度耦合且强非线性的，这造成了电磁力求解的困难，也是电磁编队研究的主要难点所在。为了在后续的构型设计与控制中取得较为精确的结果，需要合理地设计与应用电磁力模型。

电磁编队的一个应用方向是基于定常电磁力的静态构型设计。在静态构型下，编队的稳定条件是电磁力满足相对平衡态方程，各星在Hill 系下处于相对静止状态，编队整体类似单刚体航天器，稳定且高精度的控制使得编队能够完成长焦X射线成像［5］、共位衍射成像［6］、红外干涉成像［7］等空间任务。对于红外干涉成像任务，有研究为中国的觅音计划提出利用四星编队在日地L2 点组成四面体构型的大口径红外干涉望远镜的方案［8］。考虑到在深空中的编队存在距离较远、难以维护的问题，如果能将此类任务布置在近地轨道上，将有利于航天器的长期维护。但传统编队在近地轨道上受地球中心引力影响，难以维持静态构型的长期稳定。电磁编队是一种实现静态构型的方案。

对于电磁编队静态构型设计方法，早期Miller等［7］和Kong等［9］设计了五星编队构型，其中四星共线，一颗星位于线外。Hussein等［10］针对三星共面编队，设计了对齐、平行和环形3种磁矩配置模式。上述设计假设编队位于深空，忽略了地球引力因素。而在近地轨道附近，构型设计因为引力的存在而变得更加复杂。黄涣［11］和徐良［12］先后采用Kane 方法和Hamilton 方法构建电磁编队姿轨动力学模型，为双星编队设计了径、切、法3 种构型，并进一步为三星编队设计了共线和共面构型。Qi等［13］在他们的基础上进一步研究了双星编队的不变流形。Wang等［14］针对N星编队，设计了法向共线构型。总结这些研究发现，静态构型设计的关键在于找到一组满足相对平衡态方程的磁矩与位置参数，使得各星在Hill 坐标系下加速度与角加速度均为0。同时随着卫星数量的增加，电磁编队的耦合参数与平衡态方程数目迅速增加，导致构型设计难度也随之加大。为了简化问题，先前的研究通常利用同构对称性或空间降维等方式设计共线或共面编队，缺少了空间三维静态构型的设计。四星编队是最小的空间立体结构，当空间任务需要各个卫星分布在三维空间中形成立体构型时，从四星编队着手研究是个合理的选择。为了不失构型设计的一般性，研究多星异构编队。由于卫星质量不同，构型缺少对称性，这会进一步加大构型优化设计的难度。

电磁编队静态构型设计完成后，由于构型不稳定，需要设计编队控制算法。电磁编队控制可以分解为两部分。第1 部分是根据状态误差求解控制力，可以采用常规的LQR 控制器［11］、滑模控制器［15］和鲁棒控制器［16］等；第2 部分是根据控制力求解控制磁矩，可以采用的方法包括自由磁矩法［6］、最优磁矩分配法［17］、同伦延拓法［18］等。对于远场模型误差导致的控制力干扰问题，Ahsun等［19］和连克非等［20］均通过设定自适应系数，实现对控制力的实时补偿。但这样的方法是被动的、基于状态误差的反馈补偿，没有根据精确电磁力模型从控制源头主动修正磁矩来消除误差。对于近地轨道空间摄动问题，主要摄动包括地球非球形摄动与卫星面质比异构造成的大气阻力摄动等。上述的控制研究没有利用电磁力实时高精度控制的特点，没有基于已知的相对摄动模型进行前馈补偿。同时，控制研究还应考虑卫星线圈异构造成的最大磁矩不同，避免控制磁矩饱和问题。

本文主要研究异构四星电磁编队的空间立体静态构型设计与控制问题，建立了近地圆轨道附近的电磁编队动力学模型，分析了静态构型下影响编队相对运动的主要干扰项。针对空间静态构型的设计问题，推导了编队静态构型的必要条件，基于必要条件设计了一种参数降维的四面体构型，提出了利用精确电磁力模型对静态构型进行修正的方法。针对电磁编队的相对控制问题，考虑了J2 摄动与大气阻力影响，设计了摄动前馈结合滑模反馈的控制算法。数值仿真证明了四星空间静态构型设计算法、非线性修正和滑模控制器的有效性。

1 电磁编队动力学建模

1.1 相对运动的动力学建模

四星电磁编队系统如图1 所示，由4 颗异构电磁卫星构成，依次编号为1、2、3、4。每颗电磁卫星上都装有3 个互相垂直的圆形超导线圈，通电后能够产生任意调节的磁矩，进而产生星间电磁力和力矩，实现控制编队的相对运动。设编队系统质心为OCM，ρi为卫星i质心相对OCM的位置矢量。

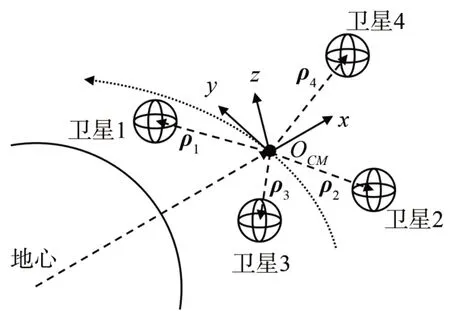
图1 四星电磁编队Fig.1 Four-satellite electromagnetic formation

对于近地轨道下的四星电磁编队，星间电磁力为编队系统内力，不会对系统质心的运动产生影响。因此，可以将编队质心作为参考点，建立Hill坐标系O-xyz，原点O位于编队质心OCM，x轴指向地心反方向，z轴沿轨道面法向，y轴满足右手法则。下文所有提到的各星相对位置、相对速度和相对加速度均是Hill坐标系下关于编队质心的物理量。

假设星间距离远小于轨道半径，则卫星i的相对运动模型可以简化为线性C-W方程：

式中：n为编队质心轨道角速度，ρi=[xi，yi，zi]T为相对位置矢量，fi=[fix，fiy，fiz]T为相对控制加速度，为相对摄动加速度。

1.2 远场电磁力模型

电磁编队研究中常假定线圈半径远小于线圈距离，从而将精确电磁力模型近似为远场电磁力模型［4］。为便于区分，符号上标EMF 表示基于远场模型，上标EME表示基于精确模型，上标EM表示两模型均可。远场模型将线圈简化为磁矩进行计算，磁矩大小的计算公式为：

式中：μ为磁矩大小，方向与电流回路满足右手螺旋定则；Nc为线圈匝数；I为线圈电流大小；a为线圈半径。磁矩方向与电流方向满足右手法则。

卫星i作用于卫星j上的电磁力和电磁力矩分别为：

式中：μ0为真空磁导率；μi，μj分别为卫星i和卫星j的磁矩；ρij为卫星j相对卫星i的位置；ρij表示卫星i、j距离大小。

根据远场模型，星间电磁力与距离的4 次方成反比，使得电磁力只适合维持近距离编队。但在近距离情况下，远场模型忽略线圈半径的前提条件不再成立，在静态构型编队中使用远场模型会造成常值偏差。下文将建立精确电磁力模型，将电磁力误差修正至零均值，作为编队高精度控制的基准。

1.3 精确电磁力模型

根据参考文献［3］，精确电磁力模型需要对两星上各个线圈的电流微元积分得到，如图2 所示。考虑到静态构型编队中各星相对姿态保持不变，为简化精确电磁力求解，假设卫星姿态由反作用轮保持稳定，卫星的三轴线圈始终与Hill坐标系三轴平行，忽略线圈厚度。

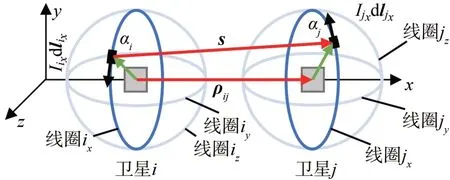
图2 精确电磁力计算Fig.2 Exact electromagnetic force calculation

图中：ai，aj分别表示卫星i，j的电磁线圈半径；记ix，jx分别表示卫星i，j垂直x轴的线圈，s为线圈ix的电流微元相对于线圈jx的电流微元的位置矢量，分别表示线圈ix，jx的电流,分别表示线圈ix，jx的电流微元指向。

线圈ix作用于线圈jx上的电磁力和力矩为：

式中：kI为与卫星i，j的线圈匝数Ni，Nj和电流Iix、Ijy相关的系数；aj表示线圈jx中心指向其上电流微元的位置矢量；μix表示线圈ix产生的磁矩大小；μjx表示线圈jx产生的磁矩大小。

为近似求得精确电磁力数值解，将式（5）写为：

式中：θix、θjx分别为线圈ix、jx上微元的角度，取值范围为[0，2π]。

卫星i作用于卫星j上的电磁力和力矩为各线圈电磁力和力矩的线性叠加：

为检验精确电磁模型数值计算方法的准确性，设定两星磁矩大小相同。在不同的磁矩配置模式下，如果随着线圈距离的增大，远场模型与精确模型之间的求解误差逐渐趋于0，则说明了精确电磁模型数值算法的准确性。这里选取了4种磁矩配置情形，如图3所示。

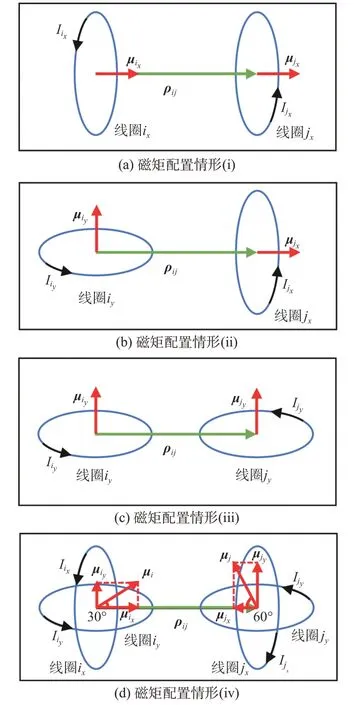
图3 四种磁矩配置情形Fig.3 Four cases of magnetic dipole configurations

根据不同离散点数下的精确模型求解结果，设定线圈距离3 m，线圈半径1 m，精确模型离散点数N=60 时的电磁力为真实电磁力，定义远场模型或精确模型的相对误差为：计算得到的电磁力与真实电磁力之差的模长与真实电磁力模长的比值。绘制精确电磁力模型相对误差与离散点数N的收敛关系，如图4（a）所示。随着离散点数增多，精确电磁力模型相对误差逐渐减小，计算精度逐渐提高。另外可以发现，情形（iii）、（iv）收敛速度较慢，原因主要在于各组微元距离变化较大，需要更多的离散点才能获得较为准确的计算结果。

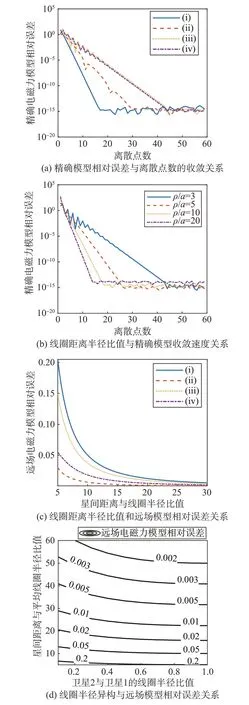
图4 精确模型与远场模型误差分析Fig.4 Error analysis of exact model and far-field model

在情形（iii）时，进一步分析星间距离与线圈半径的比值ρ/a和精确电磁力模型收敛速度的关系，如图4（b）所示。在相同计算精度的情况下，ρ/a越大，精确电磁力模型相对误差收敛速度越快。

星间距离与线圈半径的比值ρ/a与远场电磁力模型相对误差如图4（c）所示。远场电磁力模型相对误差随着ρ/a增大而减小；当ρ/a＞7时，远场电磁力模型相对误差约小于10%。

对于线圈半径不同造成的误差，在远场误差最大的情形（i）下，绘制远场模型相对误差与aj/ai、线圈距离半径比的关系如图4（d）所示，其中=(ai+aj)2 为线圈平均半径。在平均半径aˉ与相对距离ρ不变的情况下，线圈半径相差越大，远场电磁力模型误差越大。说明卫星线圈半径不同会造成更大的远场模型误差，这使得异构编队中对远场模型误差的分析显得尤为重要。

1.4 相对摄动分析

星间电磁力无法补偿编队整体受到的绝对摄动力，但能够实时补偿各星的相对摄动力，提高编队的相对位置控制精度。为分析主要的相对摄动因素，采用后续3.1 小节提到的滑模控制器对双星编队进行控制，分别保持双星的径、切、法向静态构型［11］，分析相对摄动加速度量级。

设置两星质量分别为80 kg 和100 kg，线圈半径为0.4 m 和0.5 m，迎风面质比分别为0.004 和0.005，光照面质比分别为0.009 和0.010，3 种编队下两星距离均为10 m，轨道高度500 km。将径、切、法向静态构型中卫星1所受各项相对摄动与远场模型误差干扰对比，其结果如图5所示。

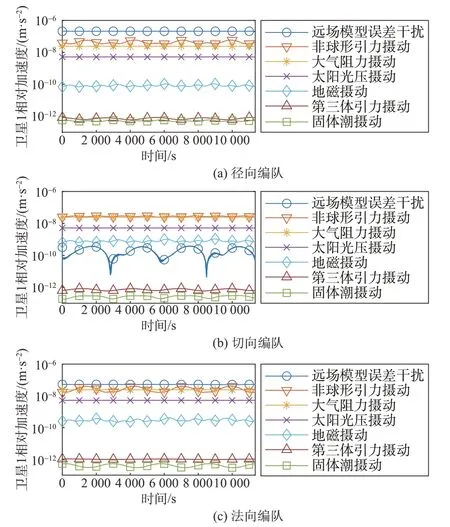
图5 电磁编队相对摄动与远场模型误差干扰比对示意图Fig.5 Comparison of electromagnetic formation relative perturbation and far-field model error

各项相对摄动量级总结如表1所示。

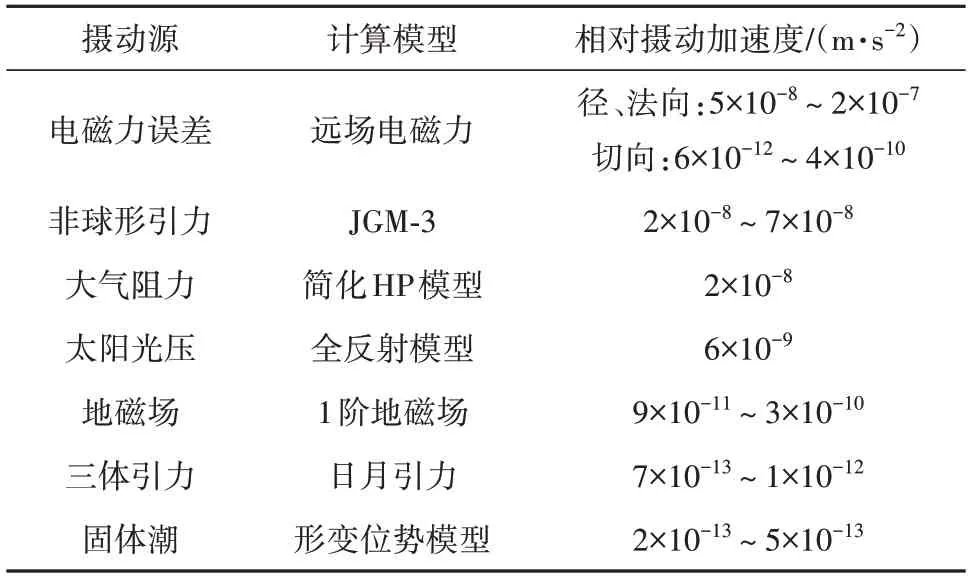
表1 静态构型编队相对摄动量级总结Table 1 Summary of relative disturbance in static formation

由表1 可知，影响编队相对运动的主要干扰项包括远场模型误差、非球形引力、大气阻力。下面简要分析这3项干扰。

1）远场模型误差

远场模型误差与磁矩大小相关。当编队为切向构型时，无需电磁力补偿地球引力主要项，产生的干扰加速度较小。当编队为径向或法向构型时，需要较大的电磁力补偿地球引力加速度偏差，并伴随产生较大的干扰加速度。

2）非球形引力

非球形相对摄动主要与卫星相对位置相关，在星间距离10 m的情况下，非球形引力可产生10-8m/s2量级的相对加速度。Hill 系下J2 项的相对摄动模型［15］如下：

3）大气阻力

大气密度根据改进HP 模型［21］选取为轨道密度，平均值7.262 1×10-13kg/m3，大气阻力相对摄动主要与卫星迎风面质比异构相关，0.001 的迎风面质比差异将产生10-8m/s2量级的相对加速度，与非球形摄动量级相当。假设各星阻力系数相同，则大气阻力的相对摄动力模型为：

2 异构电磁编队静态构型设计

2.1 静态构型必要条件

本文期望设计一种四星编队的静态构型，使得在Hill坐标系下，各星保持相对静止，相对速度与加速度均为0，此时编队呈现类似于单刚体航天器的静态构型。

基于上述静态构型定义，有：

式中：CD为阻力系数，取2.2；Kai为卫星i的面质比；Kac为编队整体面质比；ρa为大气密度；v为编队质心相对大气的速度大小为编队质心相对大气的速度方向。

4）其它摄动

太阳光压相对摄动主要与卫星受光面质比相关，0.001的受光面质比差异将产生10-9m/s2量级的相对加速度，相对大气阻力较小。固体潮、地磁场和第三体引力产生的相对摄动均较小。这些摄动在后续的前馈控制中不予考虑。

静态构型同时还要求各星相对姿态保持稳定，所以静态构型要求电磁力矩趋于0。因此静态构型需同时满足力平衡和力矩平衡方程：

在异构四星静态构型设计问题中，四星的相对位置有9 个自由度，磁矩有12 个自由度，共需满足24 个力平衡方程和力矩平衡方程，使得构型设计较为困难。为了降低系统待求参数的维数，可以分析电磁编队静态构型的必要条件，给出参数降维的构型设计方法。

星间电磁力可以线性叠加：

星间电磁力是编队系统内力，编队整体满足动量与角动量守恒：

考虑编队整体相对质心角动量守恒，将式（17）代入式（20）中的角动量守恒方程，得到：

结合式（15）、式（16）和式（21），得到满足星间内力特性的编队静态构型必要条件：

式中：Ixy、Iyz、Ixz为编队整体的惯量积，其在静态构型时须为零。

式（22）为电磁编队静态构型的一个必要条件，编队的惯量主轴与Hill坐标系的三轴平行。基于此必要条件，可以设计一类四面体构型，并用数值方法从中找出同时满足力平衡和力矩平衡的构型。

2.2 四面体构型设计

根据静态构型必要条件，设计如图6 所示的一类四面体构型：

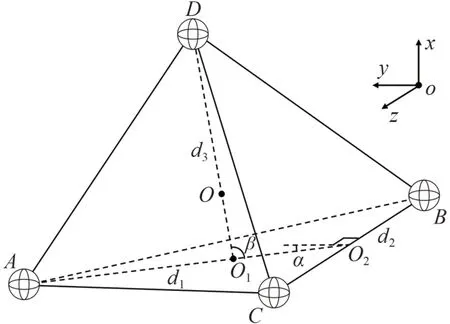
图6 四面体构型设计Fig.6 Tetrahedral configuration design

图中：卫星1、2、3、4 分别放置于四面体的A、B、C、D点，O为四面体质心，O1为ΔABC质心，O2为BC质心。以O为原点建立Hill 坐标系。AD平行xOy平面，BC平行z轴。AO2长为d1，BC长为d2，DO1长为d3，AO2与yOz平面夹角为α∈(-π/2，π/2)，∠DO1O2=β∈(0，π)。

根据上述描述计算得到编队整体相对质心的惯量积分别为：

能够使得式（23）的惯量积均为0。

上述四面体构型共有包括d=[d1，d2，d3]和α4个自由度，基于这些参数得到各星相对位置为：

通过上述四面体构型设计，将设计自由度从21维降至16维，同时也限制了构型形状为四面体。所以，电磁编队静态构型设计问题可以转换为一组含有16个自由变量和24个方程的求解问题：

式中：16个自由变量为d1，d2，d3，α，μ1x，μ1y，μ1z，μ2x，μ2y，μ2z，μ3x，μ3y，μ3z，μ4x，μ4y，μ4z。

上述求解问题由于强耦合性和强非线性，无法求得解析解，只能采用数值方法求解，例如使用L-M算法求得近似的构型数值解。

另外，结合式（3）、（15）和（30），得到电磁静态构型编队星间距离与磁矩大小的比例关系：

上式表明编队静态构型在保持形状不变的情况下，通过缩放构型尺度，并按照式（31）所示比例改变各星磁矩，所得到的新构型仍为静态构型。因此，每个静态构型都可以缩放构型尺度得到一组形状一致的静态构型解。

2.3 构型非线性修正

根据1.4 小节的分析，远场模型简化时忽略的非线性项是影响电磁编队静态构型保持的最主要因素。在静态构型设计过程中，需考虑对基于远场模型得到的静态构型进行非线性修正。将其作为初值代入基于精确电磁力模型的构型设计算法中，重新求解得到修正后的静态构型。其流程如图7所示。

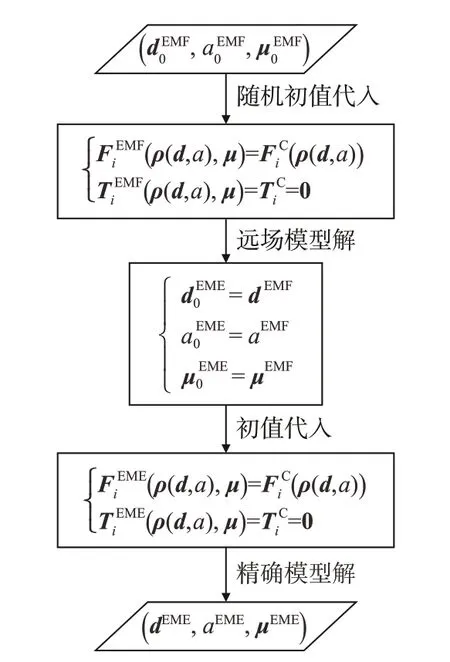
图7 静态构型解的非线性修正流程Fig.7 Nonlinear correction process for static configuration solution

为了检验非线性修正提高构型设计精度的效果，基于精确电磁力模型定义静态构型数值求解精度：

2.4 构型求解

为验证电磁编队静态构型设计方法的有效性，便于下文控制仿真，设定初始四星参数如表2所示：

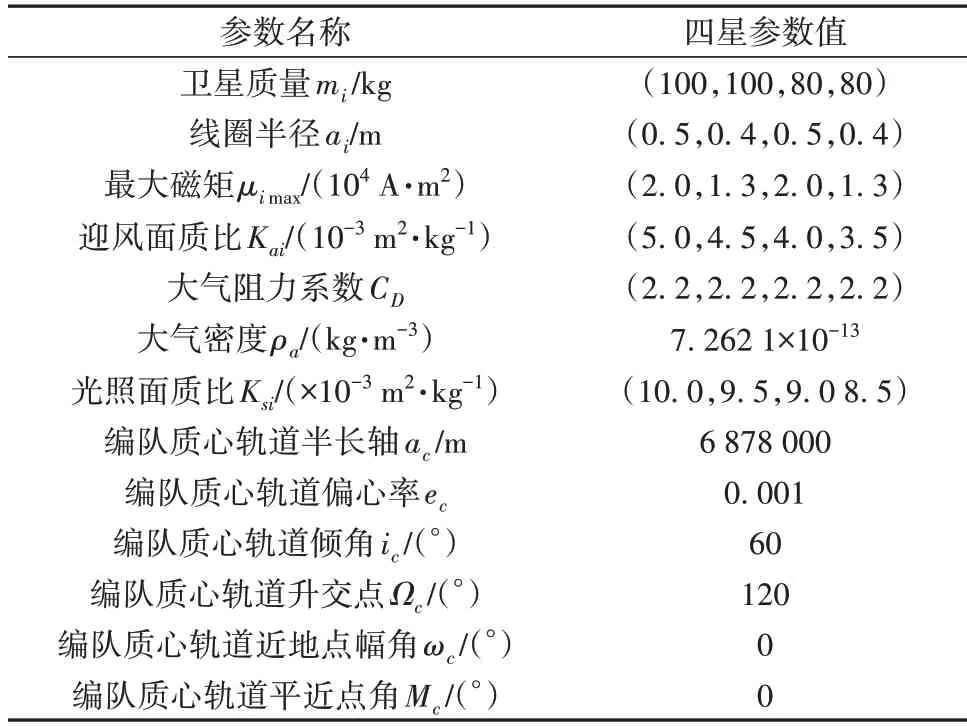
表2 四星参数Table 2 Parameters of four satellites

根据2.2 小节的分析，构型尺度等比例改变时仍然能保证静态构型，所以约束d2=10 m，简化求解过程。静态构型方程组式（30）的求解初值随机给定，通过10 000 次计算求得97 组不同的构型解。以总磁矩最小的构型为例，得到修正前的静态构型参数如表3所示：

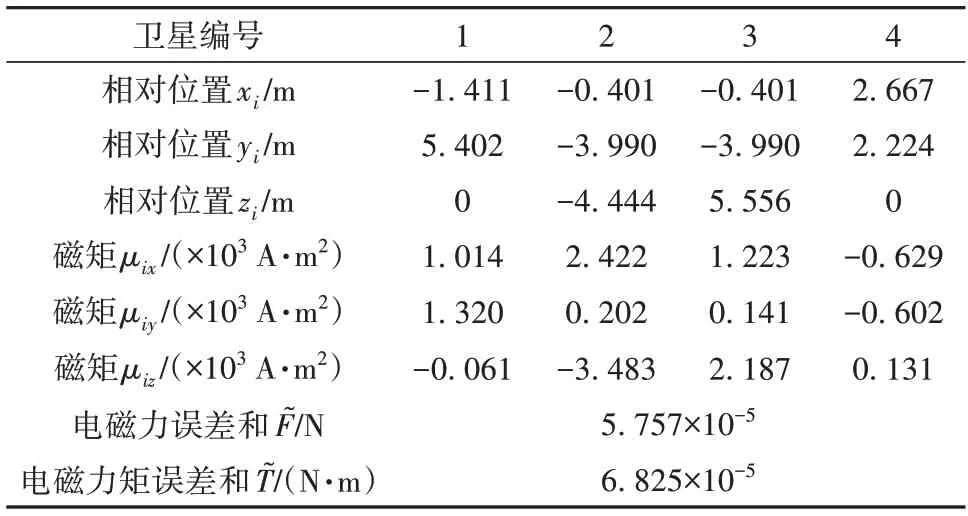
表3 修正前的静态构型参数Table 3 Static configuration parameters before correction

对构型解进行非线性修正，得到修正后的静态构型参数如表4所示：

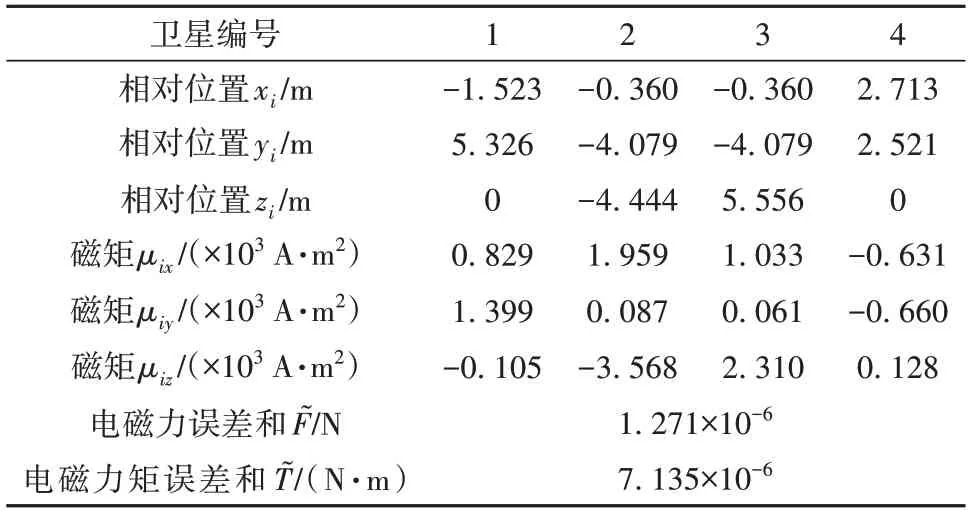
表4 修正后的静态构型参数Table 4 Static configuration parameters after correction

由表3、4可知，在上述构型下，经过非线性修正后，电磁力误差和降低了98%，电磁力矩误差和降低了90%。这说明了本文的构型设计算法给出了合理的静态构型，而且非线性修正有效提高了构型精度。修正后的静态构型如图8所示。

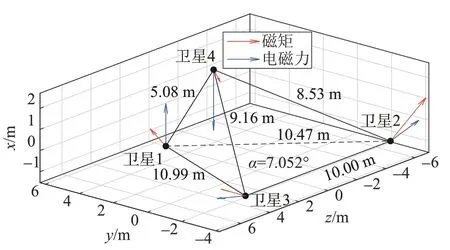
图8 静态构型示例Fig.8 Example of static configuration solution

3 电磁编队控制设计

3.1 控制器设计

为了验证静态构型设计算法的有效性，实现编队相对位置控制，结合文献［15］和［20］，设计摄动前馈结合滑模控制算法。

C-W方程式（1）可以简写为矩阵形式：

定义常系数αi＞0，设计滑模面：

模型前馈加速度Φi为：

采用指数趋近律，卫星i的控制器Ui设计如下：

式中：ηi＞0；ki＞0。为了避免抖振现象，γi(si)=[γi(six)，γi(siy)，γi(siz)]T满足：

式中：εi＞0且较小；si=[six，siy，siz]T。

考虑到需要满足四星电磁力合力为零的约束，只利用式（36）计算卫星2、3、4 的控制力，卫星1 的控制力通过式（19）得到。控制器结构整体如图9所示。

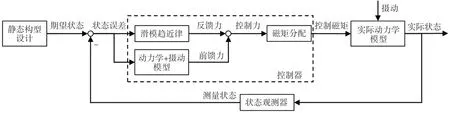
图9 电磁编队相对位置控制器结构Fig.9 Structure of electromagnetic formation relative position controller

3.2 磁矩分配优化

四星的磁矩的自由度共有12个，需要满足12个电磁力等式。但由于电磁力合力为零，减少了3 个等式，所以实际上磁矩分配问题是用9 个独立方程求解12个未知数，存在无数组磁矩解。一个求解思路是将问题转换为如下多目标优化问题：

式中：Δμi表示航天器i的磁矩与上一个控制周期的变化量；μimax为卫星i能够产生的最大磁矩。

第1 个目标希望耦合产生的电磁力矩最小，减小动量轮负担；第2 个目标限制磁矩变化量不要过大，主要原因是最优磁矩至少有互为相反数的两个解，通过添加第2个目标，使得磁矩不会在两个解之间频繁切换。

该最优问题可采用序列二次最优（SQP）算法求得磁矩数值解。为减少陷入局部最优的情况，随机多个初值计算，并且设定两个求解初值为静态构型磁矩解和上一控制周期的磁矩解。

对于远场模型误差问题，可以采用类似于图7的原理对磁矩解进行非线性修正，提高磁矩分配优化计算精度。

4 数值仿真

四星参数参考表2。仿真动力学摄动模型考虑1.4 小节中提到的所有摄动项，包括远场模型误差、非球形引力、大气阻力、太阳光压、固体潮、地磁场和第三体引力。仿真积分器采用ODE45，控制周期设置为1 s，时长设置为11 354 s（2 个轨道周期），其中0～2 000 s 用于验证编队重构至静态构型的过程，2 000～11 354 s 用于验证编队在静态构型附近的稳态控制过程。设置编队初始构型为边长10 m的正四面体，期望构型如图8 所示。控制器参数αi=0.01，ηi=10-5，εi=10-5，ki=10-2，磁矩分配优化目标权重w1=1012，w2=10-3。控制器中使用的精确电磁力模型离散点数N=10。仿真结果如图10～15所示。

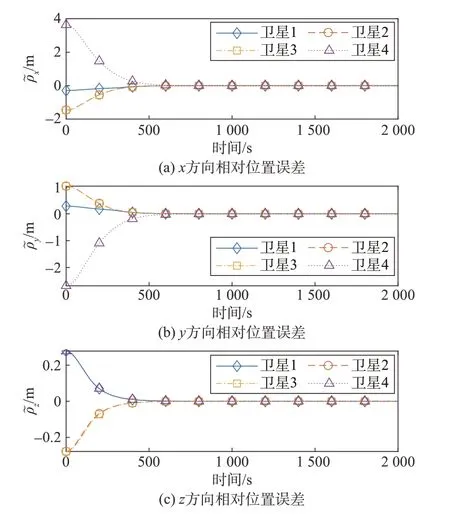
图10 四星构型重构过程Fig.10 Configuration reconstruction of four satellites

图10、图11展示了构型重构过程中各星的相对位置和磁矩变化情况，电磁编队在约600 s时接近期望构型附近，表明了设计的滑模控制器具有一定的重构能力。

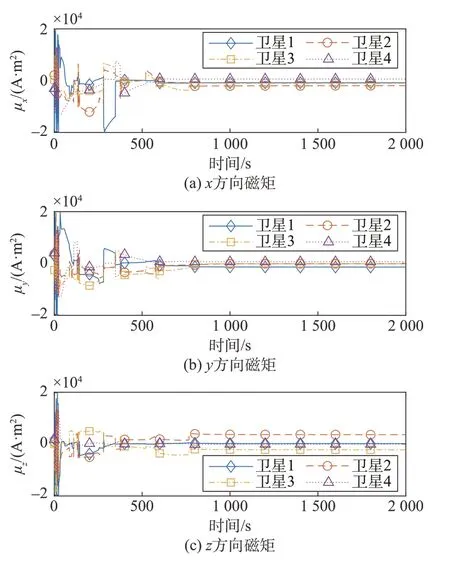
图11 四星构型重构过程磁矩Fig.11 Magnetic dipoles of four satellites in the configuration reconstruction

图12、图13 展示了各星在稳态情况下，相对位置误差不超过1×10-5m，相对速度误差不超过1×10-8m·s-1，表明了编队构型保持的高精度。

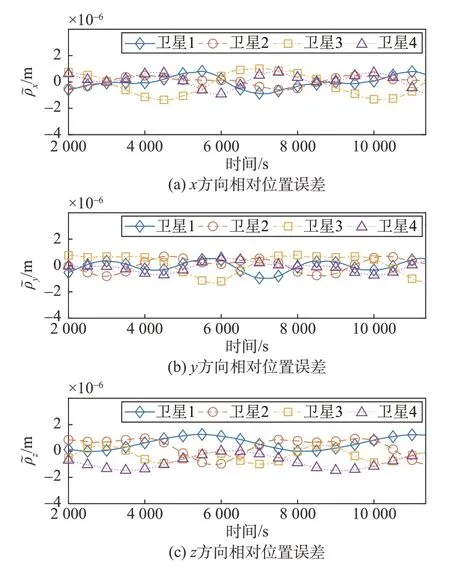
图12 四星稳态相对位置误差Fig.12 Steady-state relative position errors of four satellites

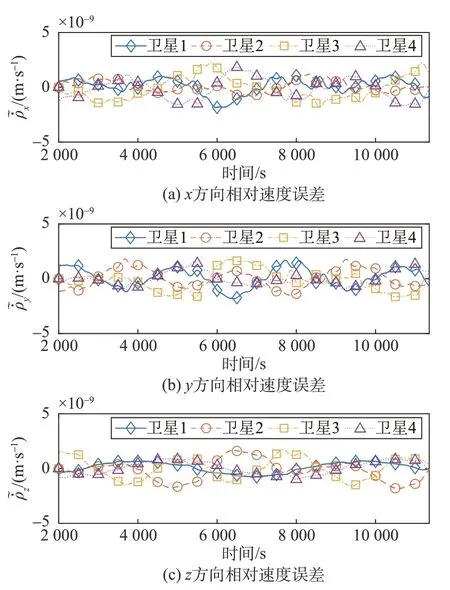
图13 四星稳态相对速度误差Fig.13 Steady-state relative velocity errors of four satellites

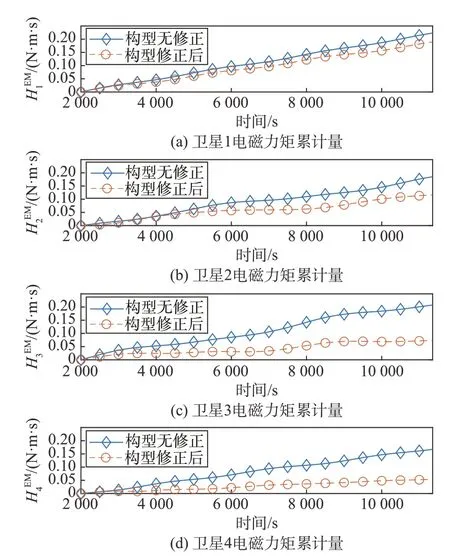
图14 静态构型非线性修正效果比较Fig.14 Comparison of nonlinear correction for static configuration

图15 说明了在第3 节设计的控制器下，控制磁矩经过精确电磁力模型修正后，平均减小了约94%的稳态位置误差。

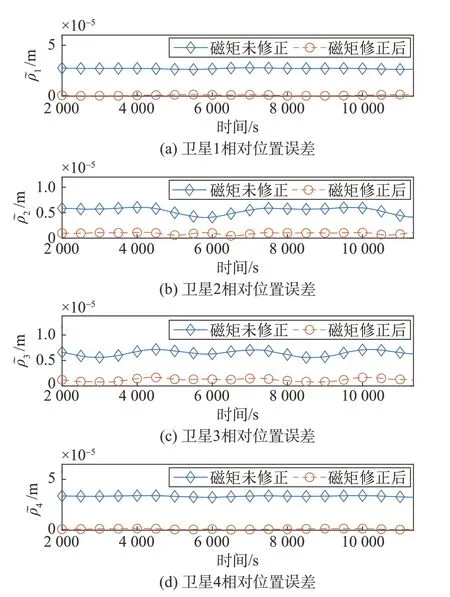
图15 控制磁矩修正效果比较Fig.15 Comparison of control magnetic dipole correction

5 结论

本文提出了异构四星电磁编队的静态构型设计与保持控制方法。主要工作包括以下3个方面：

1）对近地轨道的电磁静态构型编队所受的相对摄动力进行了分析，指出在各星相对位置存在径向与法向偏差时，远场电磁力模型误差是相对干扰主要项。

2）分析得到了静态构型编队质量分布的必要条件，并基于必要条件设计了一组四面体构型参数，显著降低了求解空间维数。通过基于精确电磁力模型的非线性修正，提升了静态构型设计精度。

3）设计了摄动前馈结合滑模控制器，并使用精确电磁力模型修正磁矩，提高了磁矩分配的准确性。

本文的空间静态构型研究基于四星编队，对于多于四星的编队，提出的编队控制算法同样适用，但也存在卫星数量增多导致的磁矩求解难度迅速加大的问题，在未来需要进一步考虑基于拓扑优化的一致性控制算法。