一种6-DOF小行星着陆轨迹序列凸优化方法

初彦峰，穆荣军，梁浩，崔乃刚

（1.哈尔滨工业大学航天学院，哈尔滨 150001；2.北京宇航系统工程研究所，北京 100076）

0 引言

作为太阳系起源的原始物质，小行星蕴含了行星形成及动力学过程的信息，其为研究太阳系演化、深空资源开发、行星防御等空间科学问题提供了重要途径［1］。小行星探测已成为当代太空争夺的新前沿，也是一个国家综合国力的体现。最初人类只能利用天文望远镜对小行星进行观测，而随着科学技术的发展，自20 世纪80 年代以来，人类已经实现了对小行星的环绕飞行及采样返回等探测任务［2］。

NASA 发射的伽利略木星探测器于1991 年对加斯普拉小行星进行了环绕飞行，这是人类第一次实现对小行星近距离探测，并于1993年飞越了编号为243的Ida小行星［3］；2018年黎明号探测器完成对小行星灶神星（Vesta）和谷神星（Ceres）的探测［4］；2020 年奥西里斯-雷克斯探测器实现了在Bennu 小行星上着陆及采样，之后其携带约250 g 样本于2023 年在美国犹他州安全着陆，这是NASA 首个小行星采样返回任务［5］。日本宇宙航空研究开发机构（JAXA）于2014年发射了国际上首颗采样返回式小行星探测器——隼鸟2号，并于2020 年实现了对小行星龙宫（1999JU3）采集样本及返回的探测任务［6］。ESA 和NASA 联合推出了小行星撞击与偏转评估计划，于2022 年利用DART 航天器撞击Didymos 小行星，以迫使其偏离运行轨道［7］。我国嫦娥二号月球探测器于2012年对Toutatis小行星进行了交会探测，拍摄了多张高清的小行星光学图像［8］。

小行星引力场建模是探测器实现精准着陆的基础。由于形状不规则，小行星附近的引力场呈现出不规则性。球谐系数引力场模型使用球形势的谐波级数展开，所以该方法对于非球形天体引力场的描述有局限性；内球谐引力场模型的收敛域可以扩展到小天体表面任意一点，但该方法仍无法使用统一表达式实现引力场的全局表征［9］。质点群法采用有限个质点填充小天体内部空间的方式进行建模，当观察点靠近小天体表面时引力场的精度会迅速退化，因此该方法并不适用于小天体表面的动力学研究［10］。多面体引力场模型可以精准地描述任意均质多面体的引力势、引力加速度和引力梯度张量，被誉为小天体引力场的优美解［10-11］。多面体引力场被视作高精准的模型，NASA 已将该模型用于433Eros小行星探测任务的规划中［12］。

着陆轨迹对探测器能否安全着陆至关重要。当探测器接近小行星表面时将处于潜在的碰撞危险中，并且探测器将着陆到地形复杂区域以采集到高价值的样本。这都要求探测器的着陆轨迹满足一定的约束条件，同时还需考虑如燃料消耗和着陆时间等性能指标。小行星着陆轨迹优化方法已经成为一个热门的研究问题。文献［13］采用内球谐引力场模型对小行星引力场进行建模，通过变量松弛和离散化处理将非凸的3-DOF 着陆问题转化为更容易求解的等效凸优化问题。文献［14］针对分段状态约束的轨迹优化问题，采用归一化方法，并引入了时间膨胀系数将其转化成为固定时间的轨迹优化问题。文献［15］提出了基于凸优化的轨迹优化方法，通过建立最小着陆误差目标函数，实现了不同飞行时间下太阳辐射压力-控制的轨迹优化，然后采用信赖域约束得到一系列SOCP 问题。文献［16］在Lambert 求解器的基础上提出了一种变飞行时间轨迹优化算法，用于解决小行星着陆过程中的燃料消耗问题。

上述方法都是基于3-DOF 的制导算法，即只涉及探测器质心的平移运动，而不考虑探测器姿态变化。3-DOF动力着陆制导起源于二十世纪的阿波罗登月计划［17］，其实现相对容易。对于平动和转动紧密耦合的未来小行星探测任务，3-DOF 制导方案可能无法满足探测器的任务需求，实现位置和姿态同步控制的6-DOF制导算法更具优势。

轨迹优化方法包括直接法和间接法。间接法采用Pontryagin 原理求解，并高度依赖于初始估计的准确性，所以使用间接法求解比较困难［18］。直接法将轨迹优化问题转化为参数优化问题，进而使用非线性规划对参数优化问题进行求解。直接法主要包括伪谱法、凸优化方法和打靶法，其中凸优化方法具有计算速度快和实时性高的特点，被广泛地应用于飞行器轨迹优化问题［19］。

本文提出一种6-DOF 小行星着陆轨迹序列凸优化方法。首先使用多面体引力场模型建立不规则小行星的引力场；通过对6-DOF 动力学模型及其约束进行线性化和离散处理，将原着陆轨迹优化问题转化为二阶锥规划问题，然后通过虚拟控制和信赖域增强算法的鲁棒性；最后通过模拟着陆433Eros小行星验证了算法的可行性和有效性。

1 小行星着陆动力学模型

1.1 多面体引力场模型

多面体引力场模型适合于描述形状不规则小天体的引力场，通过一系列三维实体来逼近小行星形状。Werner等［20］利用Gauss 散度定理推导出了多面体的引力场模型，由面引力和边引力两部分组成。不规则小行星附近空间任意一点的引力加速度可表示为：

式中：∇U(r)是引力加速度；G为引力常数；ρ为小行星密度；nf是多面体的面数；ne是多面体的边数；rf和re分别是探测器到第f个面（三角形）和第e条边的向量；Ff和Ee是和多面体形状相关的并矢对称矩阵；ωf和Le是描述计算点与多面体面和边相对关系的无量纲因子［10，16］。

1.2 小行星着陆动力学模型

本文涉及2 种与探测器运动相关的坐标系，如图1所示。

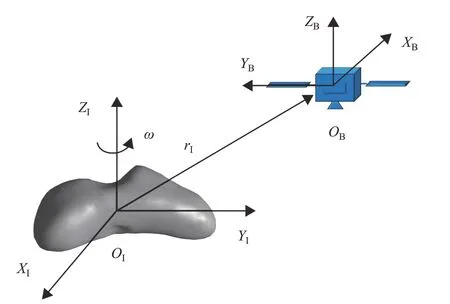
图1 坐标系的定义Fig.1 Definition of coordinate systems

小行星固联坐标系OI-XIYIZI（简写为OI系）：坐标原点位于小行星的质心，OIZI轴为小行星自转轴，OIXI轴为小行星最大惯性主轴，OIYI与OIXI，OIZI构成右手坐标系。

探测器本体坐标系OB-XBYBZB（简写为OB系）：坐标原点位于探测器的质心，OBXB，OBYB和OBZB分别为探测器的惯性主轴。

探测器的质量消耗计算如下：

式中：m(t)是探测器质量；TB(t)是探测器在OB系下的推力；α=-1 ()Ispg为质量流量系数，Isp和g分别为推力器比冲和地球标准重力常数。

探测器的动力学方程可以表示为：

式中：ω=[ω1ω2ω3]T。

四元数和欧拉角（偏航角ψ、俯仰角θ和滚转角γ）的转换关系定义如下：

1.3 状态约束和控制约束

首先探测器的质量m(t)应始终大于它的干重mdry，质量约束如下：

输出推力T(t)应介于最大推力Tmax和最小推力Tmin之间，推力约束如下：

输出力矩M(t)小于最大力矩Mmax即可，约束如下：

考虑到小行星形状不规则，并且存在着自转，探测器下降时可能会发生硬着陆现象。为了防止探测器撞击到小行星，需要对探测器的飞行路径进行约束。从距离小行星较远的位置到着陆点上方，探测器主要在小行星的外部空间飞行，因此形成包含小行星的椭球，也就是说椭球体积应大于小行星的实际尺寸。如图2 所示，最外层黄色的网格代表椭球，最里面灰色的是小行星（本文绘制的小行星是433Eros，其半长轴为16 km × 6.5 km × 6.5 km）。椭球以外的点满足≥1，整理后得到的椭球约束数学表达式如下：

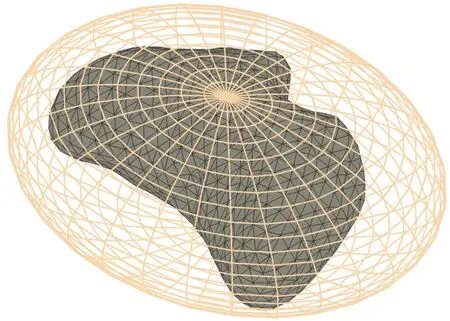
图2 椭球约束Fig.2 The ellipsoid constraint

式中：a，b，c是椭球的半长轴，由其构成的椭球要想将433Eros 小行星包围，需要满足a＞16 km，b＞6.5 km，c＞6.5 km；rI=[xyz]T是探测器位置；R是椭球半长轴形成的对角矩阵；tc为动力下降段到最终着陆段的时间。

当探测器进入到最终着陆段时，探测器与着陆点的距离足够近，则椭球约束不再适用。要实现高精度着陆，在最终着陆段需要确保探测器配备的相机能始终对着陆点进行监测。相机视野范围应该包括着陆点，也就是说相机视野范围大于相机光轴和视线向量之间的夹角，所形成的视场角约束如图3所示，定义如下：

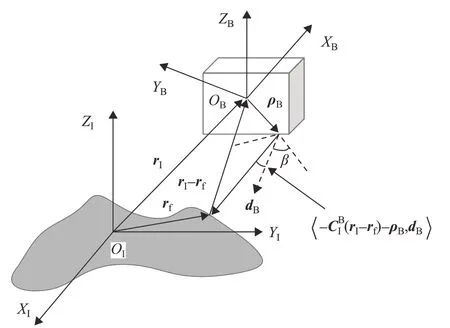
图3 视场角约束Fig.3 The field-of-view constraint

式中：β是相机视场角；ρB是相机在探测器上的安装位置；dB是相机光轴向量；tf为最终着陆时间；rI和rf分别为OI系下探测器当前位置和最终着陆位置。

2 小行星着陆序列凸优化算法

2.1 状态方程的凸化

系统状态方程式（3）及式（10）、式（11）等都是非凸的，可对其进行线性化，进而获得凸化的表达式。定义探测器的状态向量为x=[rTvTωTqT]T∈R13，控制变量为u=[TTMT]T∈R6。系统状态方程可表示为：

式（12）的线性化形式为：

式中相关的系数矩阵如下：

将探测器的状态向量分为平动状态xp=[r v]T和转动状态xr=[ω q]T，则式（13）可以分解为2 部分，如下：

其中相关的系数矩阵如式（16）～（17）所示

式中：E3代表三阶单位对角矩阵。

式中：Cω=[03×6，E3，03×4]，Cq=[04×9，E4]。

根据式（15）～（17）可得式（13）中相关矩阵的具体形式如下：

2.2 约束的凸化

引入松弛因子Γ=[ΓxΓyΓz]T代替控制力T=[ΤxΤyΤz]T，两者关系可以定义为Tj，j=x，y，z（代表估计值），则有：

对椭球约束（10）进行一阶泰勒展开，则有：

同理，对视场角约束（11）进行一阶泰勒展开，则有：

式中：h(x)计算如下：

2.3 离散化

将飞行时间[0，tf]离散化为N个子区间，设每个区间长度为Δt，则有：

系统的状态方程离散化后可以表示为：

式中：∀k∈K，K={0，1，2，…，N-1}，i代表迭代次数，相关系数矩阵定义如下：

当∀k∈Kc，Kc={0，1，2，…，Nc}，Nc=tcΔt，椭球约束离散化后：

当∀k∈Kf，Kf={Nc+1，…，N}，视场角约束离散化后：

控制力约束离散化后可以表示为：

2.4 虚拟控制和信赖域

由于对系统方程和约束进行了线性化，这样的做法将存在人为不可行性，对于飞行时间较短的轨迹优化问题可能存在不可行的解［21］。通过在线性化方程中引入虚拟控制项Vx可以解决该类问题，则式（24）可表示为：

椭球约束和视场角约束同样引入Ve和Vf，则式（26）和式（27）改写为：

将Vx，Ve和Vf加入到最小燃料消耗的目标函数中，则有：

式中：Wx＞0，We＞0和Wf＞0 为相应的权重系数；在求解过程中，虚拟控制项可视作强制惩罚项以保证算法的收敛性。

为确保线性化后能够捕获原始问题的非线性，可以引入信赖域约束使前后两步迭代之间没有明显的偏离［22］。在燃料最优的目标函数中，状态方程和约束的非线性主要是和xi(k)相关的，因此只引入状态信赖域约束即可。设第i次和i-1次的状态偏差为：

与状态相关的信赖域约束可以表示为：

上述约束引入到目标函数后，式（32）可进一步改写为：

式中：WΔ是信赖域约束的权重系数。

2.5 序列凸优化算法

经过上述凸化、离散化以及引入虚拟控制和信赖域后，小行星着陆轨迹凸优化子问题，即二阶锥规划问题（SOCP）如下所示：

式中：x0和xf分别表示初始状态和预计着陆状态；ef∈R13表示允许着陆误差；mwet和mdry分别表示探测器初始质量和探测器的净质量。

设最小状态偏差为ε，最大迭代次数为Niter，初始参考着陆参数表示为{x0(k)，u0(k)，m0(k)}，则小行星着陆轨迹序列凸优化算法流程如图4所示。

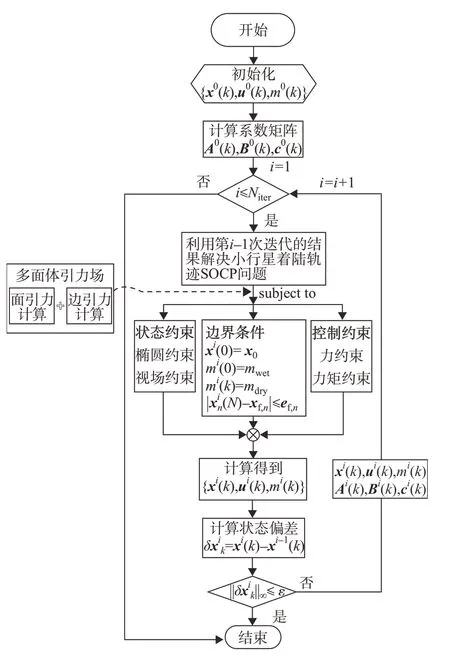
图4 小行星着陆轨迹序列凸优化算法流程Fig.4 Flow chart of sequence convex optimization algorithm for asteroid landing trajectory

首先利用初始状态x0和预计着陆状态xf计算初始参考着陆参数，然后利用其计算系数矩阵。在i小于最大迭代次数时，利用第i-1 次迭代的结果进行凸优化求解，该过程需满足状态约束、控制约束及边界条件，并且根据探测器位置矢量ri-1(k)实时更新引力加速度∇U(ri-1(k))；优化后可得到第i次迭代结果{xi(k)，ui(k)，mi(k)}，将第i-1 次结果和第i次结果进行比较，两者小于一定范围（最小状态偏差ε），可认为已经收敛并输出优化轨迹；否则以此次计算结果重新执行凸优化。以此类推，直到状态偏差满足最小状态偏差或者达到最大迭代次数。

3 仿真验证

为了快速进行序列求解，初始轨迹可利用初始状态x0和预计着陆状态xf均匀插值获取，如下：

燃料消耗会导致惯性张量发生变化，定义惯性张量更新方式，如下：

式中：Ji(k)代表第i次迭代k时刻的惯性张量；mi(k)是第i次迭代k时刻探测器质量。

为了校验所提出算法的有效性，本文以433Eros小行星为典型分析对象，它的自转角速度和密度分别为3.31×10-4rad/s和2.67×103kg/m3。仿真采用了856 个顶点和1 708 个面的小行星多面体模型，相关数据可以在PDS 网站上获取［23］。时间参数设定为动力下降段至最终着陆段历时tc=900 s 及最终着陆时间tf=1 200 s，允许状态偏差为ε=10-3，其他参数如表1和表2所示。

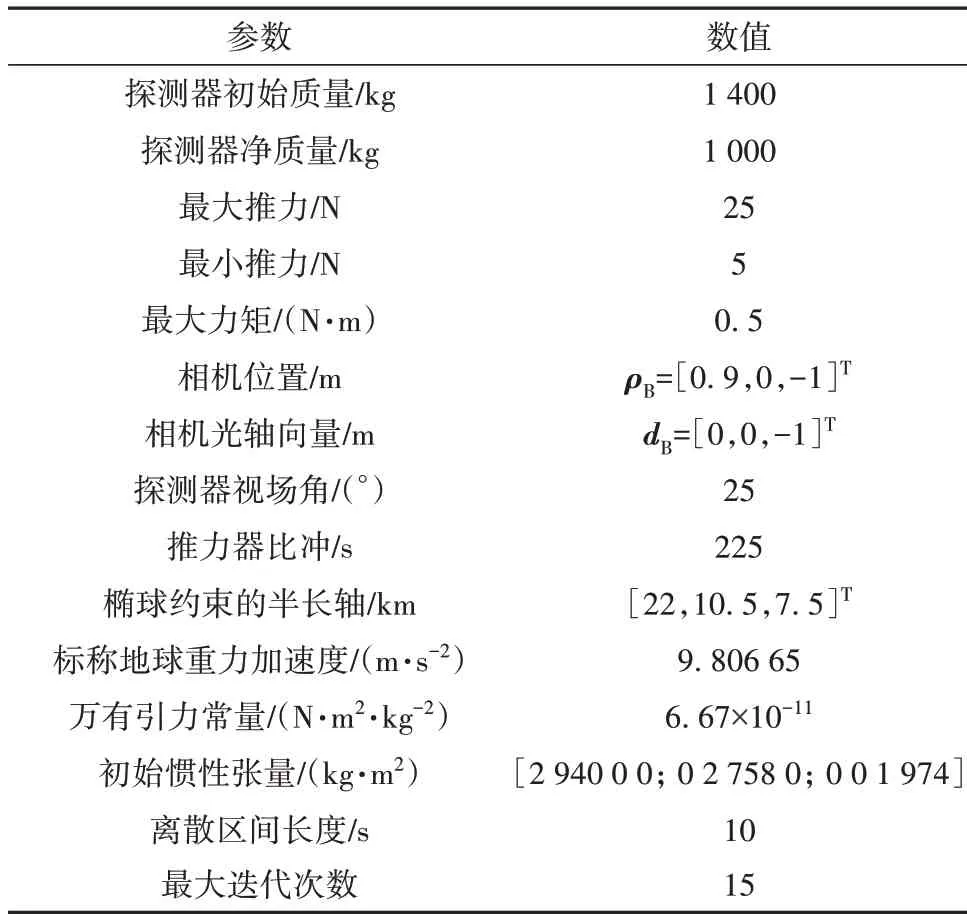
表1 仿真参数Table 1 Simulation parameters

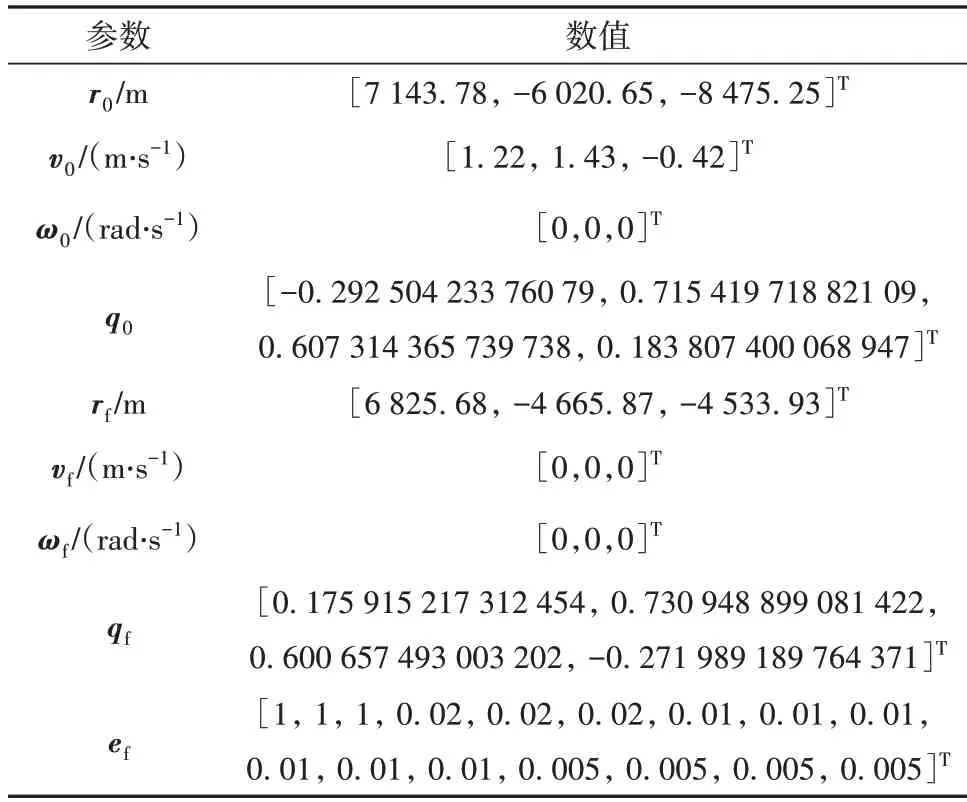
表2 初始状态、预计着陆状态及容许着陆误差Table 2 Initial state，final landing state and tolerating landing errors

本文数值模拟使用了MATLAB 软件下的CVX工具箱进行解算。根据上述模型和算法，小行星着陆轨迹序列凸优化仿真结果如图5～12 所示；为了直观地表示探测器姿态变化，本文将四元数转换为欧拉角（图8）。

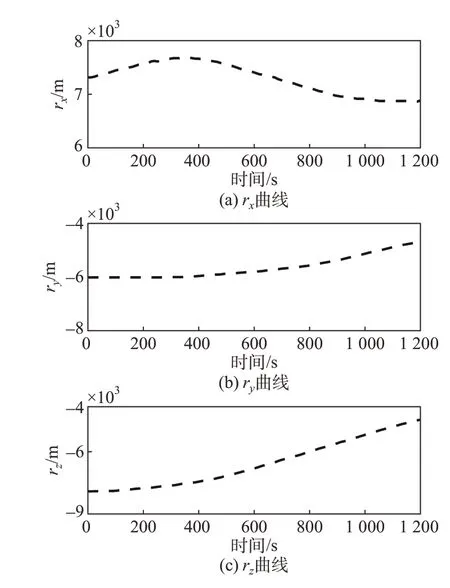
图5 位置变化曲线Fig.5 Curves of position

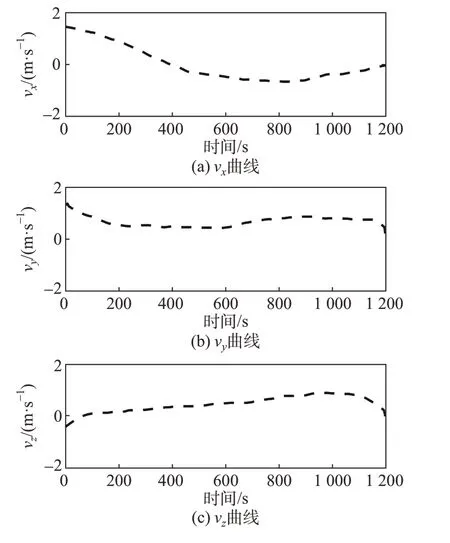
图6 速度变化曲线Fig.6 Curves of velocity

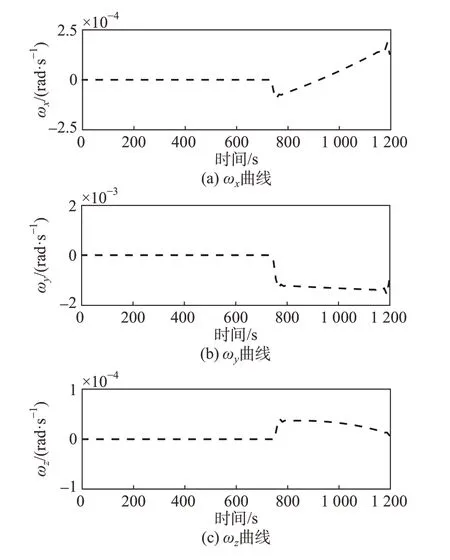
图7 角速度变化曲线Fig.7 Curves of angular velocity

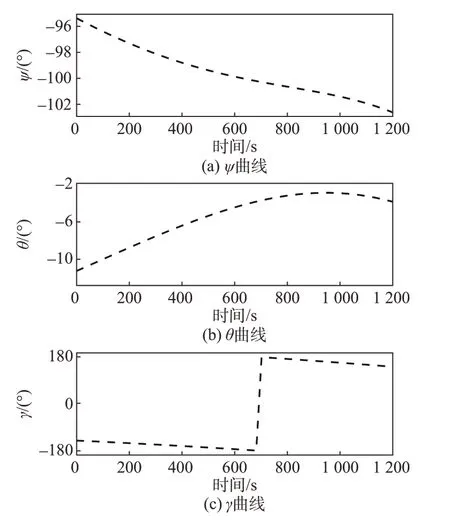
图8 姿态变化曲线Fig.8 Curves of attitude

如图5～8所示，所提出的算法可以引导探测器到达目标着陆点，探测器的最终着陆状态误差小于允许着陆误差ef，利用其优化出来的轨迹是有效的。

从图9～10 可知，探测器的推力和力矩均满足控制约束。探测器的质量变化如图11所示，最终剩余质量为1 394.8 kg，也就是说消耗燃料5.2 kg，满足质量约束。

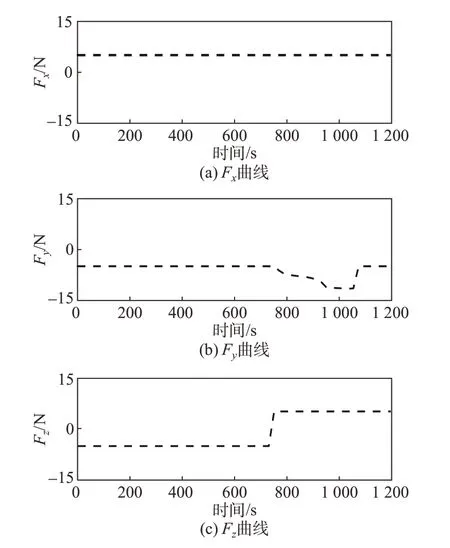
图9 推力变化曲线Fig.9 Curves of thrust

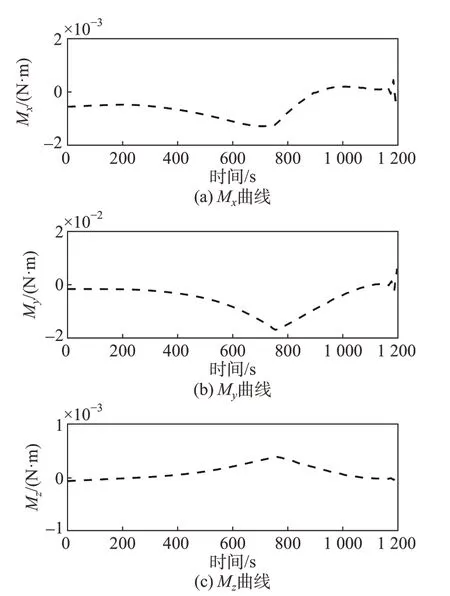
图10 力矩变化曲线Fig.10 Curves of moment

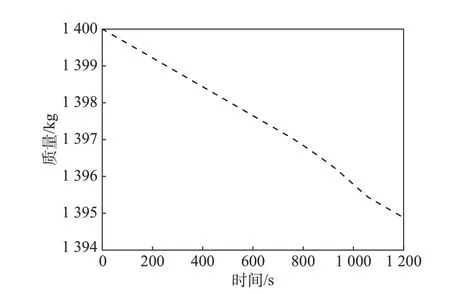
图11 质量变化曲线Fig.11 Curve of mass

式（10）表明椭球约束与探测器的位置相关，进而影响探测器着陆过程中的速度等参数；经计算，探测器的位置在动力下降段[0，tc]满足椭球约束。

式（11）表明视场角约束的作用是限制探测器姿态运动，即探测器要持续调整姿态才可以追踪着陆点；如图12 所示，探测器的视场角β在最终着陆段(tc，tf]满足视场角约束。

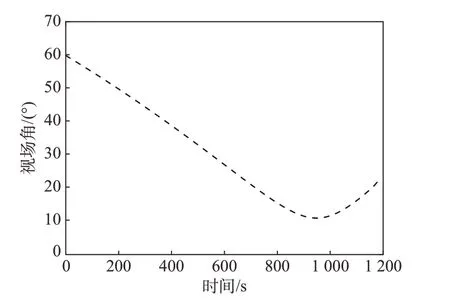
图12 视场角变化曲线Fig.12 Curve of angle of field of view

为了进一步验证轨迹优化算法对初始状态偏差的鲁棒性，本文进行了500次蒙特卡洛打靶仿真。初始位置和速度参数如表3 所示，其他未列举的参数与表1～2中相同。

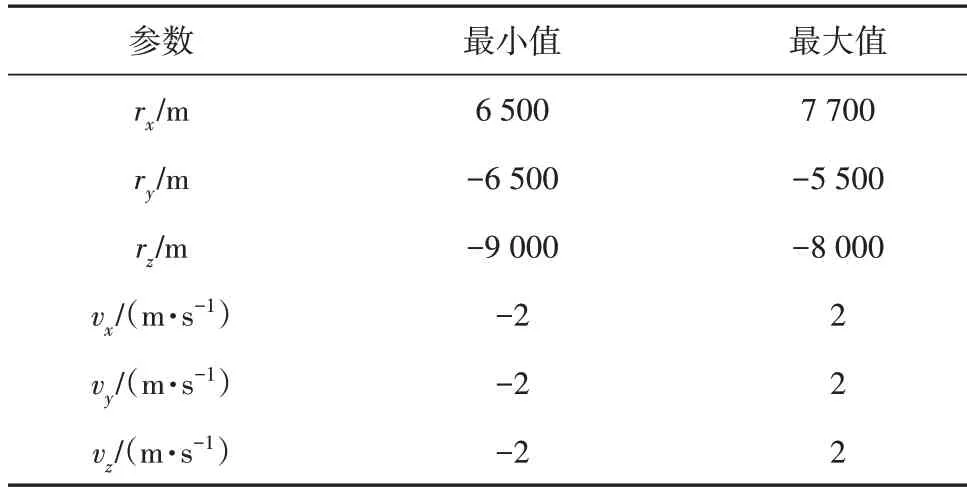
表3 蒙特卡洛打靶仿真初始位置和速度Table 3 Initial positions and velocities for Monte Carlo simulation

着陆误差统计如表4 所示，各个参数的单位与表2一致，其中最终着陆误差都达到了边界值（允许着陆误差ef）。由仿真结果可知，即使存在初始状态偏差，在制导算法作用下，探测器仍能以较小的状态误差到达着陆点，表明所提出的制导算法有很强的鲁棒性。

表4 着陆状态误差统计Table 4 Error statistics for landing state

4 结论

本文提出了一种6-DOF 小行星着陆轨迹序列凸优化算法。通过线性化和离散化将小行星着陆轨迹优化问题转化为一个可以进行序列凸优化求解的SOCP 问题；并引入虚拟控制项和信赖域，以保证线性化后采用凸优化方法是可行的。以形状不规则的433Eros 小行星为着陆目标，采用多面体引力场模型对该小行星进行引力场建模；仿真结果表明探测器能在节省燃料的同时进行高精度着陆，并满足各项约束。所提出小行星着陆轨迹优化算法可以扩展到6 自由度耦合的其他行星着陆问题，如火星或月球探测；同时，该方法精度高、鲁棒性强等优势对机载应用非常有吸引力。