关注图像信息 探寻解题思路

数学中考题对于函数的考查往往聚焦于函数的图像。我们可以通过对函数图像的直观想象，逻辑推理，挖掘出更多的内涵条件，进而解决综合型、应用型的函数问题。下面以2023年江苏省泰州市的中考题为例，谈谈如何关注图像信息，解决问题。

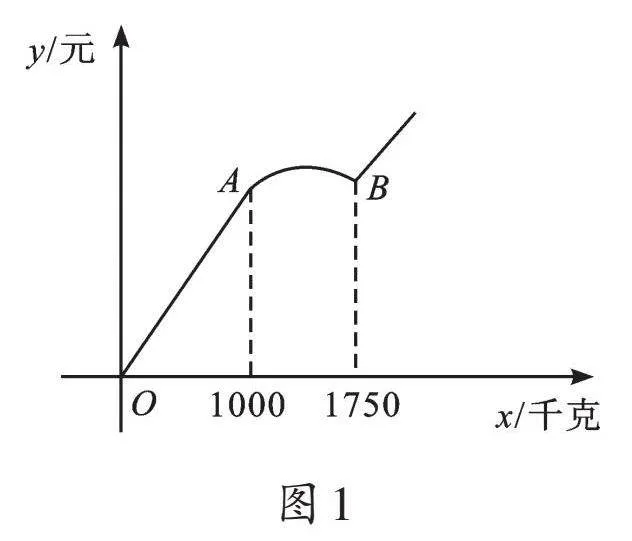
某公司的化工产品成本为30元/千克。销售部门规定：一次性销售1000千克以内时，以50元/千克的价格销售；一次性销售不低于1000千克时，每增加1千克降价0.01元。考虑到降价对利润的影响，一次性销售不低于1750千克时，均以某一固定价格销售。一次性销售利润y（元）与一次性销售量x（千克）的函数关系如图1所示。

（1）当一次性销售800千克时，利润为多少元？

（2）求一次性销售量在1000～1750kg之间时的最大利润；

（3）当一次性销售多少千克时，利润为22100元？

【分析】本题考查了一次函数和二次函数的实际应用。图像反映了一次性销售利润y（元）与一次性销售量x（千克）的函数关系，呈现出三段不同的函数。因此，我们在解决问题时要关注不同范围内的销售利润和销售量之间的关系，注意分类讨论。

解：（1）当x=800时，y=800×（50-30）=16000。

∴当一次性销售800千克时，利润为16000元。

（2）设一次性销售量在1000～1750kg

之间时，每千克商品销售利润为50-30-0.01·（x-1000）=-0.01x+30。

∴y=x（-0.01x+30）=-0.01x2+30x

=-0.01（x-1500）2+22500。

∵-0.01＜0，1000≤x≤1750，

∴当x=1500时，y有最大值，最大值为22500。

∴一次性销售量在1000～1750kg之间时的最大利润为22500元。

（3）①当一次性销售量在1000～1750kg之间时，利润为22100元，

∴-0.01（x-1500）2+22500=22100。

解得x1=1700，x2=1300。

②当一次性销售不低于1750kg时，均以某一固定价格销售，设此时函数表达式为y=kx（k≠0）。

由（2）知，当x=1750时，y=-0.01（1750

-1500）2+22500=21875。

∴B（1750，21875）。

将点B（1750，21875）代入y=kx，得k=12.5。

∴y=12.5x。

当y=22100时，22100=12.5x。

解得x=1768。

综上，当一次性销售1300kg或1700kg或1768kg时，利润为22100元。

【点评】如图2，在解决函数的应用这一类问题时，我们应结合题目条件和函数图像所给信息，将实际问题转化为数学问题，并建立函数模型，通过解决函数问题进而解决实际问题。在此过程中，应充分借助模型思想，增强应用意识。

对于函数类问题，同学们只要充分关注函数图像信息，认真分析，与题意整合，关联，充分挖掘题目中的条件，相信一定能水到渠成。

（作者单位：江苏省南京市致远初级中学）