追根析分布，变中寻本质

二次函数一直是初中数学中考中重点考查的内容，其考查范围主要包括：二次函数的概念、求解二次函数表达式、二次函数的图像及性质、二次函数与一元二次方程的关系、用二次函数解决实际问题等。现以2023年江苏省南京市中考第25题第（3）问为例，剖析一元二次方程根的分布情况的问题。

例 已知二次函数y=ax2-2ax+3（a为常数，a≠0）。若该函数的图像与x轴有两个公共点（x1，0）、（x2，0），且-1＜x1＜x2＜4，则a的取值范围是 。

【分析】二次函数y=ax2-2ax+3（a为常数，a≠0）的图像与x轴的交点横坐标是一元二次方程ax2-2ax+3=0的根，二次函数y=ax2-2ax+3过定点（0，3），且对称轴为直线x=1，由于a的符号未知，故分a＞0和a＜0两种情况讨论。

解：二次函数y=ax2-2ax+3的对称轴为直线x=1，过定点（0，3），顶点坐标为（1，3-a），二次函数y=ax2-2ax+3与x轴有两个公共点且满足-1＜x1＜x2＜4。

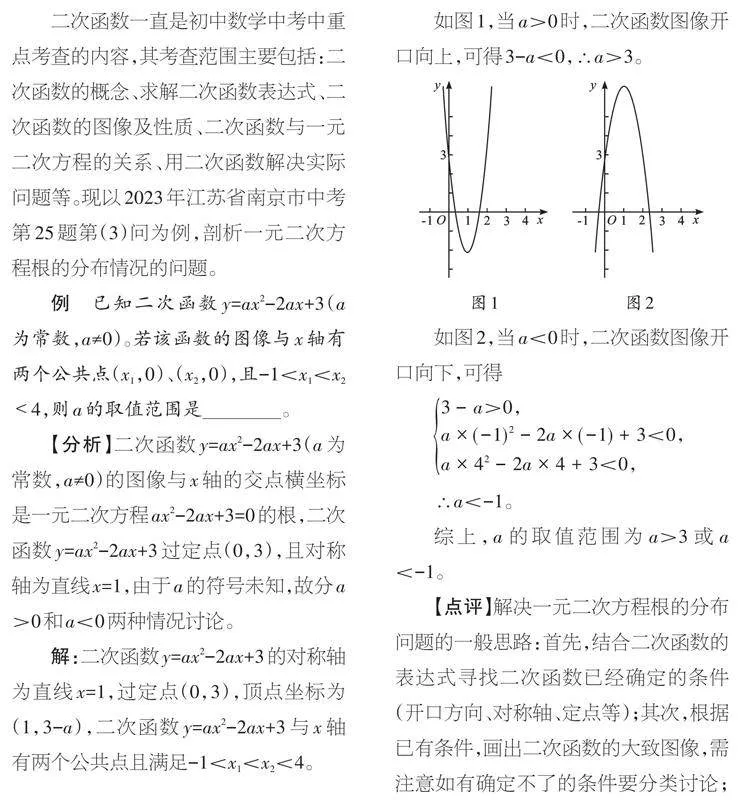
如图1，当a＞0时，二次函数图像开口向上，可得3-a＜0，∴a＞3。

如图2，当a＜0时，二次函数图像开口向下，可得[3-a＞0，a×（-1）2-2a×（-1）+3＜0，a×42-2a×4+3＜0，]

∴a＜-1。

综上，a的取值范围为a＞3或a＜-1。

【点评】解决一元二次方程根的分布问题的一般思路：首先，结合二次函数的表达式寻找二次函数已经确定的条件（开口方向、对称轴、定点等）；其次，根据已有条件，画出二次函数的大致图像，需注意如有确定不了的条件要分类讨论；最后，结合图像，以开口方向、对称轴、顶点坐标、判别式、端点处函数值等为思考方向，找到问题成立的限制条件，并正确求解。

下面我们以二次函数y=ax2-2x+3（a为常数，a＞0）与x轴有两个交点为例，改变交点的取值范围来探究交点存在的条件。

变式1 若该函数的图像与x轴有两个公共点（x1，0）、（x2，0），且x1＜4＜x2，则a的取值范围是 。

【分析】此二次函数开口向上，过定点（0，3），与x轴两个交点的横坐标一个大于4、另一个小于4，由此画出其大致图像（如图3）。

解：如图3，由题意知a×42-2×4+3＜0，∴a＜[516]。又∵a＞0，∴0＜a＜[516]。

【点评】二次函数开口向上时，如果此函数对应的一元二次方程的两个根x1、x2满足x1＜z＜x2，则应满足二次函数在z处函数值小于0。

变式2 已知二次函数y=ax2-2x+3（a为常数，a＞0）。若该函数的图像与x轴有两个公共点（x1，0）、（x2，0），且1＜x1＜x2，则a的取值范围是 。

【分析】此二次函数开口向上，过定点（0，3），与x轴两个交点的横坐标均大于1，可以画出其大致图像（如图4）。由条件“与x轴有两个公共点”，可知b2-4ac＞0或顶点处纵坐标小于0；由条件1＜x1＜x2，可知对称轴大于1，且二次函数在端点1处的函数值大于0。

解：如图4，由题意知，[（-2）2-4a×3＞0，--22a＞1，a×12-2×1+3＞0，]

∴-1＜a＜[13]。

又∵a＞0，∴0＜a＜[13]。

【点评】二次函数开口向上时，如果此函数对应的一元二次方程的两个根x1、x2满足m＜x1＜x2，则应满足对称轴大于m，b2-4ac＞0，端点m处函数值大于0。同理，两根x1、x2满足x1＜x2＜n，则应满足对称轴小于n，b2-4ac＞0，端点n处函数值大于0。

变式3 若该函数的图像与x轴有两个公共点（x1，0）、（x2，0），且1＜x1＜x2＜4，则a的取值范围是 。

【分析】已知二次函数开口向上，过定点（0，3），与x轴两个交点介于1、4之间，由此画出其大致图像（如图5）。由条件“与x轴有两个公共点”，可知b2-4ac＞0或顶点处纵坐标小于0；由条件1＜x1＜x2＜4可知对称轴在1、4之间，二次函数在端点1、4处的函数值都要大于0。

解：如图5，由题意知，[1＜--22a＜4，（-2）2-4a×3＞0，a×12-2×1+3＞0，a×42-2×4+3＞0，]

∴[516]＜a＜[13]。

【点评】二次函数开口向上时，如果该函数对应的二次方程的两个根x1、x2满足m＜x1＜x2＜n（m＜n），则应满足对称轴大于m且小于n，b2-4ac＞0，端点m、n处的函数值都大于0。

变式4 若该函数的图像与x轴有两个公共点（x1，0）、（x2，0），且1＜x1＜3＜x2＜4，则a的取值范围是 。

【分析】二次函数开口向上，过定点（0，3），与x轴两个交点的横坐标一个介于1、3之间，另一个介于3、4之间，画出其大致图像（如图6）。

解：如图6，由题意知，

[a×12-2×1+3＞0，a×32-2×3+3＜0，a×42-2×4+3＞0，]

∴[516]＜a＜[13]。

【点评】二次函数开口向上时，如果此函数对应的二次方程的两个根x1、x2满足m＜x1＜z＜x2＜n，此二次函数需满足端点m处函数值大于0，端点z处函数值小于0，端点n处函数值大于0。

（作者单位：江苏省南京市致远初级中学）