基于FPGA与STM32的双路信号源分离装置
邓星月,王琪盛,吕庆梅
绍兴文理学院元培学院,浙江绍兴,312000
0 引言
信号处理在通信中发挥着至关重要的作用,涵盖了信号的产生、传输、接收以及处理等方面。传统信号分离装置主要采用主分量分析和最大似然估计方法对混合矩阵和噪声协方差进行估计,设计模拟电路分离信号[1]。由于模拟电路存在信号质量不稳定、抗干扰能力弱等问题,本设计选择数字滤波的方法处理信号。利用FPGA电路与STM32处理器对信号进行处理,能提高运行速度、增加抗干扰能力和数据准确性[2]。本文的主要研究内容为:通过对两路信号和进行相加混合得到信号,并对混合信号进行数据采集、分析与处理,经过STM32处理器和FPGA电路,分离出信号和[3]。本装置的处理芯片采用STM32F407,其作用是调整数据采样率并进行快速傅里叶变换(FFT),得到最大频率和次大频率;FPGA电路采用EP4CE22E22A7芯片,其作用是使得信号经过两个带通滤波器后分离信号;另外,本装置通过两个数模转换器实现对两路信号的还原与显示,当混合信号波形和频率可变时,信号分离电路仍能正确分离信号。
1 系统设计分析
1.1 系统整体分析
本系统设计主要由硬件电路和软件设计两部分组成。硬件电路包括加法器、ADC08200模数转换器、基于FPGA的数字滤波器和数模转换电路,用于将、信号相加混合传输,经过处理器分离信号后数模转换输出波形[4];软件设计主要实现FFT变换、调整数据采样频率,计算、原始信号频率,并根据三次谐波和基波分量的比值,判断波形类型。最后通过液晶显示设备显示、频率、波形类型和按键设置的相位差。整体方案框架如图1所示。
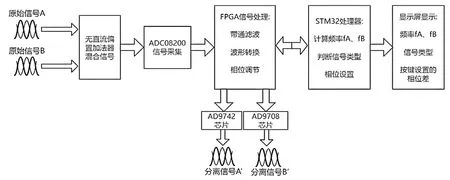
图1 系统整体方案框架图
1.2 硬件电路分析
1.2.1 无直流偏置加法器
无直流偏置加法器电路如图2所示。
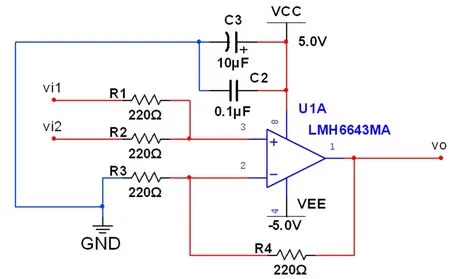
图2 无直流偏置加法器电路
偏置电路的作用是满足各级所需电位,以提供合适的静态工作点。本装置以LMH6643比例放大器为基础,采用双电源供电,输入输出偏置相同且都为交流电。由于LMH6643的偏置电流较大,所以电阻可适当调整但不宜过大。接下来利用叠加原理,分析输出信号与输入信号之间的关系:
1.2.2 ADC08200采集电路
(1)信号偏置处理
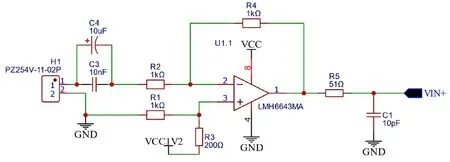
图3 信号偏置电路
(2)ADC08200转换电路
ADC08200是一个高速模数转换器,具有成本低、功耗低、体积小和易于使用等优点。采样频率高达200Msps,即使信号频率为100kHz的三角波,也同样满足采样需求。为1.2V直流电压,作为加在放大器同相端的输入。当输入为0时,电路为反相放大电路,即对端口的交流信号进行放大,放大倍数为-1;另外,当端口的交流信号为0时,电路为同相放大电路,则有以下输出公式:
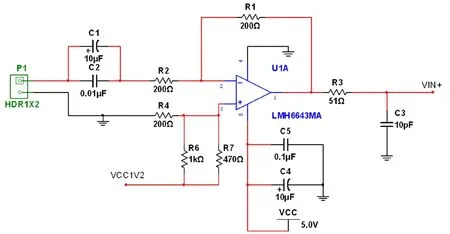
图4 ADC08200 转换电路原理图
1.2.3 信号分离处理器FPGA电路
为保证当混合信号的波形和频率可变时,本系统仍能正确分离两路信号,故舍弃模拟滤波器而采用数字滤波器实现上述功能。本系统设计的数字滤波器既能实现线性相位和相位控制,又能灵活改变滤波器的类型和参数,避免了模拟滤波器所无法克服的电压漂移、温度漂移和指标计算复杂等问题[7]。
数字滤波器时域上输入输出的关系是:
本系统采用EP4CE22E22A7作为FPGA的处理芯片,对混合信号进行数据处理和滤波,控制数字滤波器的工作范围,分离两路信号。同时,ARM板上的STM32处理器对信号处理有着同样重要的作用。首先,FPGA将AD采集的混合信号经过采样率为2048K的带通滤波器,使得STM32对其进行2048点数的FFT变换,点与点频率间隔为1K[8]。FFT输出的模的最大值为,次大值为。STM32负责计算信号频率、波形类型和按键设置的相位差,最终通过串口发送给FPGA。FPGA已知、之后,将频率信号分别经过两个带宽小于5K,采样率分别为、的带通滤波器[9],得到正弦信号,信号分离初步完成。为便于区分和理解FPGA和STM32两者的工作范围,制作了如图5所示的分工区域图。
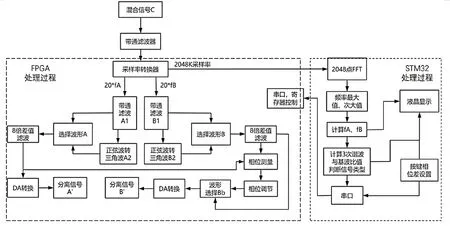
图5 FPGA 和STM32 的分工区域图
1.2.4 数模转换电路
由于本系统是将混合信号分为两路信号,故需要两个数模转换芯片分别对输出信号进行转换,并在示波器上显示无失真波形。考虑到转换速率问题,本装置选用AD9742(12位分辨率)和AD9708(8位分辨率)两种芯片,其转换速率都高达210Msps,完全满足分离模拟信号的带宽要求。系统中的两路数模转换电路,AD9742位于ARM核心板上;AD9708位于扩展DA电路上,接下来以AD9742芯片为例分析数模转换过程。
根据AD9742数据手册,本芯片可选择片内或片外参考电压,本设计选用片内1.2V参考源,且,。接下来开始计算各输出电压、电流值:
设计如图6所示的DA转换电路,其中VOUTA与VOUTB分别为差分放大电路的反相输入端和同相输入端,且放大电路采用1.2V直流偏置。利用叠加原理分析计算如下:
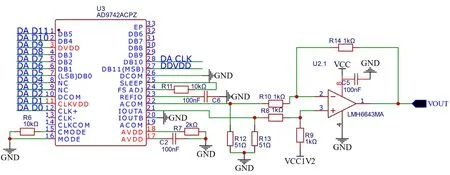
图6 DA 转换与差分放大电路
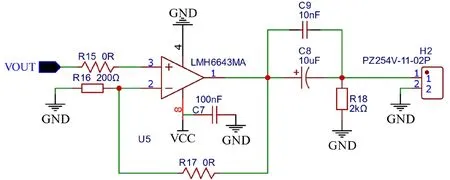
图7 DA 输出调理电路
1.3 软件设计分析
软件设计将硬件电路采样和处理的数据信号进行程序算法,计算相应指标以及数据分析。STM32主要完成的步骤是:①对采样后的混合信号进行2048点数的FFT变换;②分别计算正弦波、三角波的三次谐波和基波分量的比值,判断波形类型;③对分离信号进行8倍插值滤波,动态控制相位差。其具体逻辑过程如图8所示。
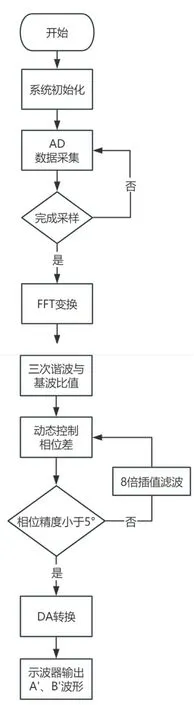
图8 软件设计流程图
1.4 主要功能模块程序设计分析
1.4.1 FFT变换与波形判断
另外,函数FFT返回值的数据结构具有对称性,所以在实际计算时,的取值范围为。FFT输出结果的模的最大值和次大值,即为初始信号、的频率,其中最大值为信号的频率,记为;次大值为信号的频率,记为。
对于波形判断来说,正弦波只有基波分量,而三角波具有快速衰减的奇数次波分量,主要为基波和三次谐波。通过计算两个波形的三次谐波和基波分量的比值,即可快速分辨出波形类型。
1.4.2 设置与控制相位功能
信号精度提高后,对其进行初相位差公式计算[10],计算公式如下:
2 测试结果与分析
2.1 实际电路测量结果
2.1.1 固定频点正弦波分离
结果如图9、图10所示。在研究双路信号的分离过程时,已通过多组实验结果验证本系统的可行性,这里列举两组数据详细说明。当A、B信号为固定频点正弦波时,第一组信号分别为50kHz、100kHz,峰峰值均为1V的正弦波,经系统分离后,得到分离信号分别为50.136kHz、99.576kHz,误差均在5%以内;再来看第二组数据,当原始信号分别为90kHz、100kHz,峰峰值为1V的正弦波时,得到分离信号分别为89.968kHz、99.880kHz,误差低于2%,分离结果更精确,完成还原信号的目的。
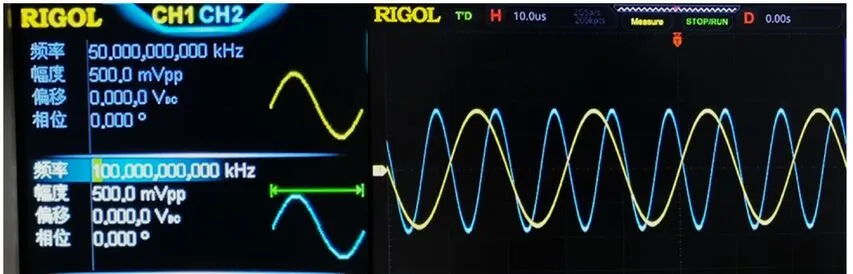
图9 固定频点正弦波信号参数设置
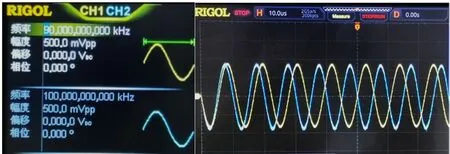
图10 固定频点下的正弦波信号分离显示
2.1.2 可变频点正弦波/三角波分离
结果如图11、图12所示。在研究不同波形、频率的信号分离时,需对双路信号进行相关参数设置。从上述两组数据来看,第一组信号为60kHz、峰峰值为1V的正弦波,=90kHz,峰峰值为1V的三角波。分离出信号为60.210kHz、为89.972kHz,误差均在5%以内;第二组信号为95kHz、峰峰值为1V的正弦波,=100kHz,峰峰值为1 V 的三角波。分离出信号为95.038kHz、为99.815kHz,误差降至1%以内。
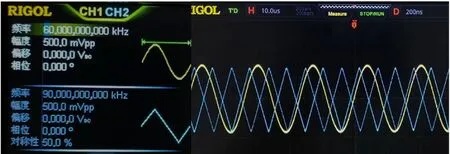
图11 可变频点双波形信号参数设置
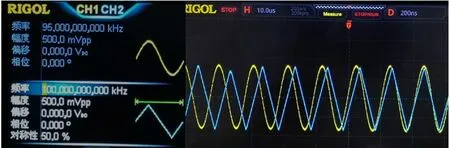
图12 可变频点下的双波形信号分离显示
2.1.3A´与B´初相位差的设置
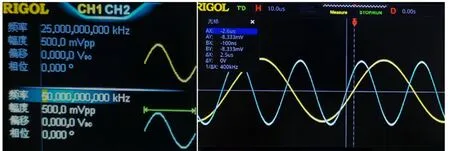
图13 固定频点下的双波形信号参数设置
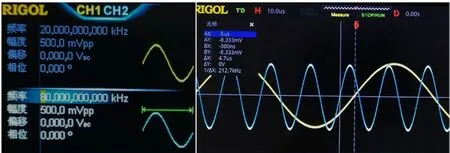
图14 A´与B´初相位差的输出波形显示
2.2 测量数据分析
2.2.1 双路正弦波信号分离测量数据
通过多组双路正弦波信号数据验证了本信号分离装置的可行性,其中信号、的频率范围在20~100kHz,峰峰值为1V保持不变。从测量结果来看,分离出的信号与原始信号误差均在5%以内,达到精度要求,如表1所示。

表1 双路正弦波信号测量结果数据对比
2.2.2 正弦波/三角波信号分离测量数据
本组数据验证了不同波形、频率对信号分离装置的影响,其在20kHz和100kHz的临界频率时,信号误差均在1%以内,具有良好的信号分离能力。且从前文提到的输出波形上来看,均可输出连续稳定的不失真波形,如表2所示。

表2 不同波形信号测量结果数据对比
2.2.3 设置A、B初相位差的测量数据
本组数据验证了在不同波形下,设置A、B初相位差对信号分离装置的影响。从数据结果上来看,输出信号A´与B´的初相位差误差均在1%以内,满足精度要求,实现了按键设置与控制初相位差的作用,如表3所示。

表3 不同波形的初相位差测量结果数据对比
3 结语
本文设计了一款基于FPGA数字滤波器的双路信号源分离装置,通过加法器混合信号、AD采集、数字滤波、DA转换,实现了波形、频率可变,分离两路信号的过程。相较于传统电路,采用STM32与FPGA配合工作,极大地弱化了电路的复杂程度,提高了运行效率,增加了数据准确性,对日后深入研究信号分离系统具有一定指导和参考意义。

