基于岭回归的动态死亡率预测方法及其改进

李雨欣

(南开大学金融学院, 天津 300350)

得益于社会经济发展与医疗条件的不断改善,人类寿命不断延长。据国家统计局政府公开信息,截至2022年末,全国60岁及以上人口28 004万人,占总人口的19.8%。其中65岁及以上人口为20 978万人,占14.9%。人口增长与经济发展之间存在着密切联系,既可以具有相互促进的关系,也可能形成相互制约的局面。人口死亡率关乎社会养老保障、商业养老年金、长寿风险等的管理。随着我国人口老龄化程度的进一步加深,对于人口死亡率的建模尤为重要。而当前较为流行的对死亡率历史演变的大部分模型都是使用按年龄、时期和队列(或出生年份)分解死亡率进行的。这3个变量形成了一种自然的方法,可以分析个人的死亡率如何随着年龄的增长而变化、医疗和社会进步随时间的影响,以及个人从出生起对终身死亡率的影响。本文在年龄-时期-队列(age-period-cohort,APC)模型的估计方式上进行推广,在广义线性模型(general liner model,GLM)的基础上使用岭回归改进APC模型,以解决APC模型所存在的共线性问题,并对日本总人口数据进行建模分析、评价与预测。

1 文献综述

当前国内外学者对于模型的选择多采用动态死亡率模型,即随机死亡率模型。随机死亡率模型的研究起源于Lee-Carter模型,该模型使用包含年龄与日历年的死亡率数据,根据这两个变量建立死亡率模型,将日历年作为一个时间序列进行预测,从而获得对死亡率的未来预测结果。Lee-Carter模型随后衍生出许多变体并得到了广泛应用,RH(Renshaw-Haberman)模型就是其中之一,RH模型向Lee-Carter模型中引入描述了出生年效应的参数,通过将时期和队列参数作为时间序列,进行预测后可以进一步获得死亡率的预测结果。这一改进显著提高了模型的拟合与预测效果。随后,为解决RH模型的稳健性,Currie等[1]对模型进行了简化,形成了仅包含年龄、时期、队列效应,而不包含交互项的年龄-时期-队列(APC)模型,该模型对美国历史数据有很高的拟合度。在应用于随机死亡率估计之前,APC模型已在人口学和医学的领域中得到了广泛的应用。然而,APC模型具有完全的多重共线性。Fosse和Winship[2]对APC模型的点估计进行了总结,认为解决APC模型完全的多重共线性的方法可分为两大类:一类是使用明确的约束,如将两个类别相关的效果设置为彼此相等;另一类是使用机械约束,如岭回归、偏最小二乘回归和主成分回归等。Olaniran和Moyosola[3]对APC模型进行了岭回归改进后,结合蒙特卡洛模拟法对法国总人口死亡率进行模拟,证明了岭回归改进具有良好的效果。Hunt和Blake[4]对APC模型的可识别性问题进行了全面分析,并讨论了如何预测死亡率模型,认为可识别性问题涉及确定性趋势,这些趋势必须通过额外的任意可识别性限制在3种效应中进行分配。Hunt和Blake[5]随后回顾了迄今为止提出的APC模型,分析了APC死亡率模型的结构,列出了使用这些模型构建时应考虑的关键原则。

相较之下,国内对于人口死亡率的研究相对较少。旷开金等[6]运用灰色预测模型GM(1,1)以及3层BP(back propagation)神经网络结构模型,分别对福建省人口死亡率进行建模预测。赵明等[7]使用灰色预测模型,改进了Double-Gap方法对寿命差距进行建模,并将预测结果与传统 Double-Gap 方法、Lee-Carter模型和贝叶斯分层模型进行比较。赵明[8]采用多人口Li-Lee模型对人口死亡率进行联合预测,并将预测结果与单人口Lee-Carter模型进行比较,以探寻适合中国人口死亡率预测的模型方法。周华林等[9]采用ACF(0)模型、 多人口Lee-Carter交叉分类可信度模型和单人口Lee-Carter模型预测人口死亡率,并运用人口-发展-环境(population-development-environment ,PDE)分析模型预测我国人口老龄化变动趋势。

2 理论模型

2.1 随机死亡率模型

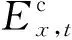
(1)

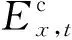
(2)

Lee和Carter在1992年提出的随机死亡率模型的构成如下:

lnmx,t=αx+βxκt

(3)

式中:mx,t为年龄为x的人在日历年t的死亡人数;αx为对数死亡率随年龄x的变动;κt为对数死亡率随日历年t的变动;βx为年龄对日历年的敏感度。通过对κt进行时间序列预测可以对模型进行外推。

Renshaw和Haberman[10]向Lee-Carter模型引入了队列效应,将模型拓展为包含出生年参数γt-x的随机死亡率模型:

(4)

该模型除年龄、时期以及队列效应参数以外,还包含了年龄随时期、队列的交叉项,计算相对复杂。Currie等[1]对RH(Renshaw-Haberman)模型进行了简化,使模型变为仅包含的年龄、时期、队列效应的APC模型:

lnmx,t=αx+κt+γt-x

(5)

以上随机死亡率模型的估计与预测均可分为两步,首先是对模型参数进行估计,即使用数据进行拟合,随后对包含时期效应与队列效应模型的两种参数使用时间序列的方法进行预测,从而得到预测的死亡率。

2.2 拟合方法——广义线性模型拟合

使用泊松分布的广义线性模型对APC模型进行拟合较为常见,但由于存在多重共线性问题,需另外添加约束条件以使模型可被识别。假设拟合模型包含na个年龄,ny个日历年,因此有n=nany个观测值。

设X=[Xa:Xy:Xc],其中Xa为代表年龄效应的n×na维的矩阵,由ny个na维的单位矩阵堆叠而成;Xy为代表时期效应的n×ny维的矩阵,由na个ny维的单位矩阵堆叠而成;Xc为表示队列效应的n×nc维的矩阵,该矩阵的列为队列效应的nc个出生年,则对于第n个观测值,即该矩阵的第n行,除该观测值的出生年所在列的位置为1外其余元素为0。此外,定义1p为由p维元素均为1的列向量,Iq为维度为q的单位矩阵。因此X矩阵可以表示为克罗内克尔积的形式:X=[1ny⊗Ina:1na⊗Iny:Xc]。易知矩阵X的秩比其行数少3,模型是不可被识别的。

将对应于矩阵Xa的系数列向量设为α,对应于矩阵Xy的系数列向量设为κ,对应于矩阵Xc的系数列向量设为γ,则广义线性模型估计式的系数列向量为θ=(αT,κT,γT)T。为使用最大似然估计法,需要为这个估计式添加限制条件。Currie[11]提供了下列方式:

(6)

将这3个限制条件写为类似于X的矩阵形式,即

(7)

将表示限制条件的矩阵H作为限制矩阵,并入到矩阵X中,即

(8)

式中:Xaug为得到的增广矩阵,Hθ=0。因此如果Xaug是满秩矩阵时,θ有唯一解。

然而R语言中的gnm函数无法对参数的相互关系进行设定,只能够设定某几个参数的限制条件,因此使用一种不同的设定,κ1=γ1=γnc=0,它的限制矩阵为

(9)

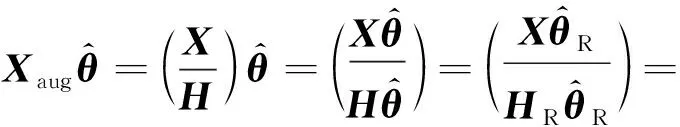
(10)

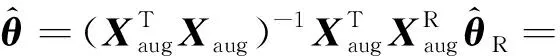
(11)

这样即可得到符合限制条件的系数值。

2.3 泊松岭回归估计

泊松岭回归估计(Poisson Ridge regression,PRR)能够消除模型存在的多重共线性。在解的矩阵中添加一个k倍的单位矩阵,尽管会使模型发生偏移,但可以很好地消除其多重共线性。PRR估计量在死亡率模型中可以定义为

(12)

式中:W为由死力μx,t构成的对角矩阵;k为一个非负的常值;I为单位矩阵。当k=0时岭回归估计量将会变回为最大似然估计量,k值越大,模型的方差越小,偏差越大。此时的回归系数可以表示为

(13)

本文主要使用均方根误差、似然函数和贝叶斯信息准则进行评价。

(1)均方根误差(RMSE)的计算公式为

(14)

(2)似然函数的计算公式为

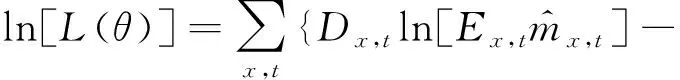
(15)

式中:L(θ)为似然函数的估计值。通常来说,似然函数的值越大,模型拟合效果越好。

(3)贝叶斯信息准则(BIC)的计算公式为

BIC=-2ln[L(θ)]+klnN

(16)

式中:k为模型中所使用的参数的个数;N为观测样本的个数。BIC的值越小,表明模型的拟合效果越好。

3 实证分析

3.1 数据说明

鉴于我国仅有1994—2021年共计28年的数据,时期跨度很小,且1996年日历年数据末组为“85+,”1995—2015年的隔5年全国1%人口抽样调查数据末组为“100+”,其余年份均为“90+”。部分死亡人口数据存在空缺值,同时文献[8,12]指出人口普查在低龄和高龄期存在不同程度漏报,尤其是新生儿死亡数据漏报严重。因此本文选取1980—2020年日本两性人口0～95岁数据、使用1980—1999年的死亡数据作为训练集进行建模并拟合,使用2000—2020年数据作为测试集进行预测,数据来源于人类死亡率数据库(Human Mortality Database,HMD),数据时间跨度达40年,且缺失值较少。

3.2 模型拟合结果

分别使用Currie[11]带限制条件的广义线性模型与附加岭回归的改进模型对数据进行拟合并对比其效果。

首先,应用R语言中的gnm(广义非线性模型)包中的gnm函数来对APC模型进行估计,并设定死亡人口数服从泊松分布、总人口暴露数为偏移量、连接函数为对数函数。当形式为线性的模型进入gnm函数中,gnm函数退化为glm函数,即广义线性模型函数。但gnm函数的优势在于可以添加单个参数的限制条件,即上述理论模型中的3个参数为零。在使用gnm函数时,需添加constrain ="[?]"的参数以弹出窗口对κ1=γ1=γnc=0的条件进行设定。

随后将最大似然估计得到的系数进行矩阵运算以得到预测的死亡率、RMSE,并将系数分解为3种效应。使用交叉验证的方式得到k值,设定k值的区间为0～1,对步长为0.001的k值进行计算,得到使RMSE最小的k值作为最优值,随后代入到模型中得到总体死亡率的拟合。为提高计算效率,使用网格搜索的方式对k值进行求解:在(0,1)的区间内首先设定步长为0.1计算RMSE,选取使RMSE最小的k值,记为k(1),随后,可在(k(1)-0.1,k(1)+0.1)的区间内,设置步长为0.01进行搜索,得到使RMSE最小的k值,记为k(2)……依次类推,直到得到满足精度下的k值。

表1中为改进模型与原模型评价准则的对比,均方根误差、似然函数、贝叶斯信息准则3个评价准则中岭回归改进的模型相较于广义线性模型均表现良好,可见岭回归模型在拟合效果上起到了改进的作用。

表1 模型拟合效果比较

3.3 模型预测

分别对两种方法的参数κt与γc进行时间序列预测。图1给出了75、80、85、90岁总人口的死亡率。从图1中能够看出,对于高龄数据,岭回归方法的预测效果明显优于最大似然方法。且随着估计年龄的提高,越来越接近真实的粗死亡率数据。而对于每一选取年龄的预测,岭回归估计的预测结果都要优于广义线性模型的估计。

图1 1980—2020年日本75、80、85、90岁人口死亡率

4 结论

对随机死亡率APC模型的估计方式进行改进,引入岭回归估计模型,并基于日本1980—1999年0～95岁人口死亡率,分别使用广义线性泊松回归模型,与改进的岭回归模型进行死亡率的拟合,随后对2000—2020年的0～95随人口死亡率进行预测,并与真实值进行模型评估准则比较。实证分析结果表明,在拟合效果与预测结果上,改进的岭回归模型优于使用最大似然估计的GLM模型,尽管会造成一定的估计偏移,但会使模型均方根误差、似然函数与贝叶斯信息准则得到显著改进。本文的不足之处在于,对于死亡率的拟合除假设死亡率服从泊松分布以外,还可能假设死亡率服从二项分布,是否能够提出该方式的岭回归改进模型尚待进一步研究。