B样条函数法似计算方法

张友华,袁 波*,徐子杰,郑世宇

(1.贵州大学 空间结构研究中心,贵州 贵阳 550025;2.贵州大学 贵州省结构工程重点实验室,贵州 贵阳 550025)

B样条函数法是基于变分原理和B样条为基础建立的数值计算方法,作为一种良好的逼近工具,被应用于分析工程中的各类结构。样条函数方法不仅拥有通用有限元法的许多优点,包含计算精度高、系数矩阵具有对称性、适应不同边界条件等;基于B样条的优异性能,该方法还具有计算量更小、更易于计算机程序编制等优点。随着科学技术的进步,工程对于数值计算方法要求更精确,实际情况中结构承受的荷载并非线性分布,因此,基于样条函数法研究结构受任意分布荷载的数值计算方法具有现实意义。

1946年,美国数学家I.J.Schoenoerg首先提出B样条函数。1976年,国内外学者开始将B样条函数用于结构分析,并提出了多种样条函数方法。石钟慈[1]基于三次B样条及变分法推导出样条有限元法,分析各种边界条件的板梁组合弯曲问题。秦荣[2]基于B样条、三角函数及能量法提出样条有限点法,分析弹性薄板受均布荷载弯曲问题。此后,秦荣[3]在样条函数的基础上提出样条边界元法、样条子域法、板壳分析等新理论新方法,并用于规则结构及非规则结构的分析求解。秦荣在文献[4]中阐述样条函数法中结构受集中力、均布荷载、线荷载、任意荷载的数值积分方法。此后,多位学者在文献[2]中对样条函数法及任意荷载的计算方法进行了大量的研究。

此前,基于最小势能原理,运用B样条函数的分部积分公式计算任意荷载函数与B样条位移函数乘积的积分,该方法存在计算高次B样条函数构成的基函数运算量大、处理复杂荷载不便、编程工作量大等问题。在本文中,提出使用n次Lagrange插值多项式构造需求的荷载函数,发挥多项式与样条函数的乘积便于数值积分的特性,简化荷载列阵的计算,本方法的具体步骤和数值积分公式均在算例中体现。参考文献[5-10]中的算例,基于样条函数法解圆柱壳问题时,由于坐标轴建立的特殊性,结构自重荷载与环向坐标位置为三角函数关系,且可同文献中的计算结果进行直接比较,验证本方法的误差大小,故取文献[6]相同尺寸的圆柱壳算例。

1 样条函数方法解圆柱壳结构

1.1 位移函数

图1为圆柱壳结构模型,坐标轴x和y布置在板的中性平面内,坐标原点布置在圆柱壳的顶端角点上,取x轴沿壳体中曲面的环向,y轴沿壳体中曲面的纵向,z轴沿壳体中曲面的法向。结构在x与y方向上的长度分别取为a和b,则取值范围可表示为0≤x≤a及0≤y≤b。沿x方向及y方向分别作均匀划分为N段、M段,本文选择以三次B样条函数乘积的线性组合作为结构的位移函数。表示如下:

(1)

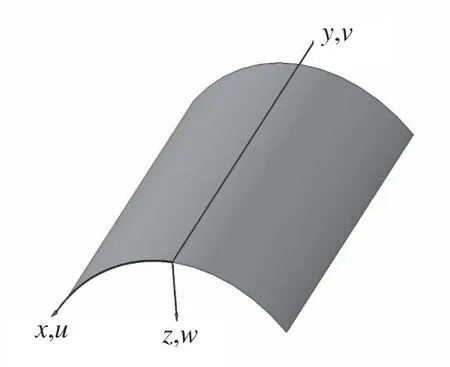
图1 圆柱壳结构模型Fig.1 Structural model of cylindrical shell

现将(1)式写成矩阵形式:

(2)

(3)

上式(2)、(3)中,ψ⊗φ表示矩阵ψ与φ的Kronecker乘积,aij、bij和cij为样条线点参数,φi(x)和ψj(y)都是与三次样条函数有关的基函数。

其中,

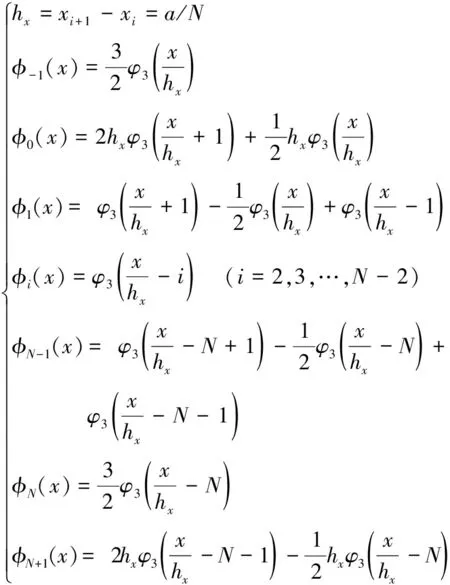
(4)

1.2 样条基函数

本文选用如下φi(x)基函数,(ψj(y) 基函数也选用如下相同格式,只需改hx为hy,改N为M),如下所示,式(2)的φ可以写成

φ=ΦQ

(5)

其中,

(6)

(7)

式中,I为(N-3)行(N-3)列的单位矩阵,样条基函数组合系数矩阵Φ=φ3(x/h-i)为三次样条基函数,Q为(N+3)行(N+3)列的样条基函数组合系数矩阵。矩阵Ψ与矩阵φ的构造方式相同,且选用相同样条基函数组合系数矩阵Q(只需把hx改为hy)。

1.3 薄板的基本方程

论文假设薄板中平面应力与弯曲应力互不影响,薄板的基本方程则由平面问题的基本方程和弯曲问题的基本方程组合而成。

1.3.1几何方程

位移函数采用(1)式所示的双三次样条函数的形式,则几何方程为

(8)

其中,

(9)

(10)

(11)

1.3.2物理方程

(12)

式中,D和R都是弹性矩阵。对于正交异性板壳及各项同性板壳,D和R为

(13)

其中,

(14)

(15)

当板壳各项同性时,则式(14)(15)简化为:

(16)

(17)

式中:Ex、Ey、Rx、Ry及μx、μy为x,y方向的弹性模量及泊松系数,d为板壳厚度;Nx、Ny、Nxy为壳体的薄膜内力;Mx、My、Mxy分别为壳体的弯矩和扭矩。

1.4 圆柱薄板的总势能泛函

(18)

式中:Π为圆柱壳拱的能量泛函;U为位移向量,q为荷载向量。

将式(8)、(12)带入圆形薄板总势能泛函方程(18)中,可以将其改写成如下形式:

(19)

运用变分原理可以得到

Gδ=f

(20)

其中,

(21)

(22)

1.5 板块的刚度方程

式(20)为圆柱壳的总刚度方程。现将式(21)、(22)展开,得

(23)

(24)

(25)

本文对以上公式符号做出了如下定义

(26)

2 荷载列阵的数值积分

2.1 基于Lagrange插值的近似计算

由图1中可知,圆形薄板任意位置处的自重荷载q均可以沿圆形薄板分解为切向和法相的荷载,则x,y,z方向的荷载可用函数表示,即

(27)

将上式(27)带入式(24)中,得

(28)

在此处设Lagrange插值逼近的函数如下式:

(29)

式中:Pn(x) 表示正弦函数的n次Lagrange插值多项式;Ln(x)表示余弦函数的n次Lagrange插值多项式。

将式(29)带入式(28)中,得

(30)

依据n次Lagrange中插值多项式函数的特点,式(30)荷载列阵在x方向上的积分项可展开为

(31)

式中:an和bn分别为插值多项式Pn(x)及Ln(x)中幂函数xn的系数。

因此,只要求出每一项进行累加即可得到目标函数在区间上的定积分。

由式(5)及(31)可以得到下式:

(32)

2.2 数值积分公式

上式中矩阵Φ中的每一项是三次B样条函数,由B样条函数的数值计算特性可知,单独对B样条函数进行多重积分与多次求导是易于得出结果的,因此,可运用分部积分法建立下列积分公式对式(32)中每一项进行计算得到荷载列阵的值(依据本文需要,取到四次Lagrange中插值多项式函数),其中,每一项的数值积分方法如下所示。

在区间[0,a]上N等分,令t=(x/hx-i),通过换元法积分,则可得到下式:

(33)

(34)

再运用分部积分法对式(34)中每一项进行数值计算得到下式:

(35)

基于B样条函数φn(x)的求积分公式便可计算式(35),积分公式如下所示:

(36)

式中:B样条函数φn(x)右上角负号表示求积分次数。

2.3 构造插值多项式

在考虑逼近曲线的光滑性、连续性、易于编程等特点后,本文选用二次、三次及四次等不同Lagrange插值多项式逼近正弦及余弦函数。由于结构从坐标原点处开始,沿x正负方向荷载变化规律一致,其逼近区间选为[0,π/2],其插值节点与插值多项式如下表1、表2所示,插值多项式函数图如图2所示。

表1 正弦函数插值节点与插值多项式Tab.1 Sinusoidal function interpolation nodes and interpolation polynomials

表2 余弦函数插值节点与插值多项式Tab.2 Cosine function interpolation nodes and interpolation polynomials

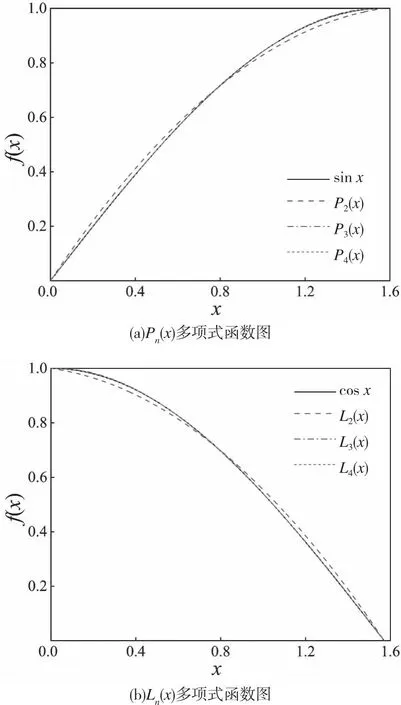
图2 插值多项式函数图Fig.2 Interpolation polynomial approximation rendering

正弦函数插值多项式的具体表达式如下式所示:

(37)

余弦函数插值多项式的具体表达式如下式所示:

(38)

3 数值算例

圆柱壳拱屋顶承受自重荷载。圆柱壳直线边界自由。参考文献中的算例,为同其他计算方法作比较,本文中算例曲线边界约束设置为简支,其结构及尺寸如图3所示。依据结构对称的受力特性,取对半结构进行计算,网格划分为10×10的网格。本方法计算结果与相关文献方法及精确解(扁壳解法)结果比较见表3和图4,与精确解(扁壳解法)的相对误差见表4。

表3 特殊点的位移和内力Tab.3 Displacement and internal force of special points

表4 特殊点位移和内力的相对误差Tab.4 Relative error of displacement and internal force at special points

图3 结构尺寸Fig.3 Structural dimension diagram

图4 内力分布图Fig.4 Internal force distribution diagram

综合分析上述算例结果,如表4所示,二次、三次、四次插值方法在特殊点处的相对误差均低于1.5%,均满足工程要求的计算精度,且三次、四次插值方法的误差低于二次插值方法,结合图2中三次、四次插值函数逼近效果优于二次插值函数分析,表明两者之间存在着一致性。如图4所示,三种插值方法的位移与内力沿不同方向上的分布均与精确解(扁壳解法)一致。

4 结论

本文发展了一种插值逼近形式的数值计算方法求解结构受任意荷载问题。基于样条函数法及Lagrange插值法,推导了近似计算方法的数值积分公式,并通过解圆柱壳结构算例详细展示了本方法的具体步骤。通过文中算例分析,得出以下结论:

1)本文使用三种不同插值多项式得到解与精确解(扁壳解法)及相关文献解对比均具有较高计算精度,证明了本方法能够有效分析结构受任意荷载问题。

2)近似计算方法以n次Lagrange插值多项式作为荷载函数,具有与原函数相同的光滑性、连续性、单调性等数学特性。本文基于Lagrange插值法的灵活性,取不同插值节点构造了三种不同的插值多项式,基于其具有的广泛适用性,对两种不同分布荷载均构造了插值函数,说明本方法对于任意荷载均具有较强适用性。

3)本文通过插值逼近的方法及多项式与B样条函数乘积易于数值积分的思路,用近似函数替代原荷载函数,从而优化计算流程,解决复杂荷载不便于积分运算的问题。为未来研究结构受任意荷载问题提供新思路,具有广阔的发展和应用前景。