利用勾股定理求立体图形的最短问题

王爱玲

空间几何体中的最短路线问题，往往是先转化为平面内的最短路线问题，可先画出方案图，然后确定最短距离及路径图。对于几何题内问题的关键是将立体图形转化为平面问题求解，然后构造直角三角形，利用勾股定理求解。

方法总结。1.解决立体图形中最短距离问题的关键是把立体图形平面化，即把立体图形沿着某一条线展开，转化为平面问题后，借助“两点之间，线段最短”或“垂线段最短”，进而构造直角三角形，借助勾股定理求解。

2.平面图形的最短路径通常是作轴对称变换，转化为“两点之间线段最短”的模型来解决问题。常见的有圆柱体的展开、长方体的展开、楼梯的展开、绕绳的展开等等，下面我们就通过一些典型的例题对这些问题逐一讲解。

题型一 用展开图求长方体中的最短问题

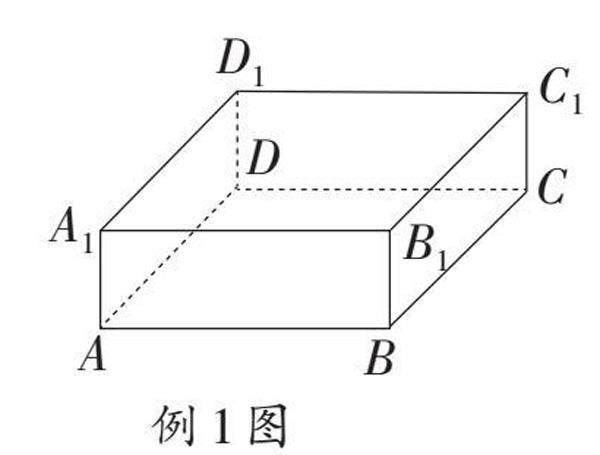
例1 （2022秋·南关区校级期末）如图，一长方体木块长AB=6，宽BC=5，高BB1=2.一只蚂蚁从木块点A处，沿木块表面爬行到點C1位置最短路径的长度为（）

A.[89] B.[85] C.[125] D.[80]

【分析】连接AC1，求出AC1的长即可，分为三种情况：画出图形，根据勾股定理求出每种情况时AC1的长，再找出最短的即可。

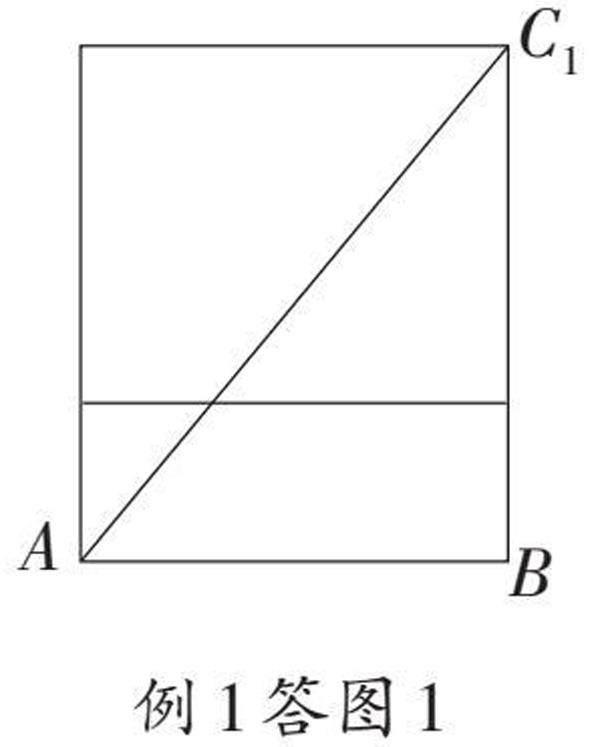
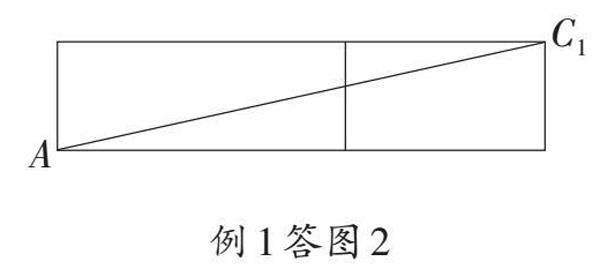
【解答】解：展开成平面后，连接AC1，则AC1的长就是绳子最短时的长度，如图1，由勾股定理得：AC1=[85]（cm）；如图2，由勾股定理得：AC1=5[5]（cm）；如图3，同法可求AC1=[89]（cm）。∵[85]＜[89]＜5[5]，∴最短路径的长度为[85]cm。

题型二 用展开图求圆柱体的最短问题

例2 （2022秋·惠济区校级期末）一只蚂蚁从圆柱体的下底面A点沿着侧面爬到上底面B点，已知圆柱的底面周长为12cm，高为8cm，则蚂蚁所走过的最短路径是        cm．

【分析】将圆柱体展开，利用勾股定理进行求解即可。

【解答】解：如图，线段AB即为所求，由题意得：∠ACB＝90°，AC＝6cm，BC＝8cm，∴AB=10（cm）。即蚂蚁走过的最短路径为：10cm。故答案为：10。

【点评】本题考查了平面展开——最短路线问题，勾股定理的应用。圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，高等于圆柱的高，本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决。

学会把几何体表面展开成平面图形，找到最短路径。通过展开图形，构建直角三角形，运用勾股定理求出最短路径。过程与方法：通过动手操作，找到最短路径；画出展开后的平面图形，把实际问题转化成用勾股定理能解决的数学问题。情感态度与价值观：能灵活运用数形结合的思想，提高运用勾股定理解决实际问题的能力，培养归纳总结规律的能力。