基于深度强化学习的汽车零件生产车间AGV节能调度算法
荣子鸣
(新疆大学商学院,乌鲁木齐 830000)
0 引言
AGV(automated guided vehicle)[1],是指装备有电磁或光学导引装置,以电池为动力,具有运行、停止、安全保护等多种功能的自动引导小车。随着智能制造在制造业企业的不断推进,作为智能制造关键性设备的AGV 在以汽车零件生产车间为代表的各种产品生产车间中的应用越来越广泛,受到行业内研究者的广泛关注。2021 年,我国提出了“碳达峰”“碳中和”理念。工业[2]作为降碳节能的主战场,要平衡好自身发展与节能减排之间的关系。作为工业重要组成部分的汽车制造业也积极响应降碳节能,AGV 的引入大大助力了降碳节能的推进,AGV 完全由电力驱动,本身没有碳排放,是较为环保的运输工具。但市场竞争的加剧,汽车零件生产车间承担的生产任务越来越多、引入的AGV 越来越多,AGV 调度场景逐渐由已知所有任务转变到任务动态生成。传统的AGV 调度算法难以适应这些变化,将AGV 任务分配和路径规划分开计算,导致AGV 路径规划解效果不佳,完成所有任务所行驶路程过长,浪费了大量电力,此外,导致多AGV 调度场景中发生碰撞冲突的次数大大增加。
目前,上述车间多AGV 调度中所存在问题的研究已取得了较大的进展。张宇航等[3]提出了一种基于改进A*算法的路径规划方法,通过提高算法效率节约了能源。魏刘倩[4]构建了一种基于灵活时空网络模型的AGV 节能路径规划办法,并根据模型设计了一种双层启发式算法进行求解,得到了有效的节能路径规划解并证明了优越性。张中伟等[5]提出了一种基于粒子群优化算法的AGV 节能路径规划算法,降低了AGV 完成所有任务的耗能。郑晓军等[6]建立了以软时间窗为约束的多车型AGV优化配送模型,最后使用遗传算法对其求解,成功降低了能耗。王唯鉴等[7]采用了一种基于多智能体强化学习的多AGV 任务分配方法,优化了车间多AGV 任务分配的流程。Krell 等[8]提出了一种融合可视图法的粒子群优化算法,成功降低了能耗。Zhang 等[9]提出了一种改进A*算法,大大降低AGV 完成所有任务需要的行驶里程,从而节约了能源。Du 等[10]建立了一种改进的遗传节能路径规划算法,并进行了对比实验验证它的优越性。Hu 等[11]提出了一种带基准线的节能路径规划方法,并设计仿真实验验证该方法的有效性。Zhu 等[12]提出了一种DQN(Double Deep Q Network,Double DQN)算法多AGV 节能路径规划算法,降低了AGV在未知环境下的能量消耗。
但是现有的研究仍然存在一些问题,目前大部分研究将节能指标聚焦在完成所有任务时间和路径长度[13]上,将碰撞冲突次数也作为节能指标的研究较少。此外,目前现有的AGV 节能调度算法多采用传统的启发式算法,如A*算法[3,9]、Dijkstra 算法[14]、粒子群优化算法[5,8]、遗传算法[6,10,15-17]。这些算法无法适应当前动态生成任务的AGV 调度场景,而对适用动态环境的深度强化学习算法研究较少。此外,现有的研究大多将AGV 调度中的任务分配和路径规划分开计算,联合计算AGV 任务分配和路径规划的AGV调度算法研究较少。
因此,本文建立以最小化完成所有任务的最长行驶路径(以下简称最长路程)和碰撞冲突次数(以下简称冲突次数)为目标的汽车零件生产车间多AGV 节能调度模型,并提出了一种改进的Double DQN 算法对模型进行求解,最后在仿真环境中验证算法的有效性并且与遗传算法进行对比,证明基于改进Double DQN 的车间AGV调度算法的优越性。
1 问题描述与数学模型
1.1 问题描述
目前汽车零件生产车间中,位于停靠区可使用的AGV 数量为k,其编号集合K为{1,2,3,…,g,…,k}。其停靠点集合o为{o1,o2,o3,…,ok},停靠点ok坐标为(Ax0k,Ay0k)。车间中的各个区域会先后生成的搬运任务数为n,由k辆AGV 从各自停靠点ok出发去协同完成。但由于生产的持续性,同一时间里,汽车零件柔性生产车间中最多同时存在的待完成任务数量为m(m<n),可以得到一个任务最大个数为m的动态待完成任务列表M,一个长度最大值为m的动态待完成任务列表I={I1,I2,…Ii,Ij,…,Im},新产生的任务为Im+1,Im+2,…,In。列表I中第i号任务记作Ii,其起点记作Iis,坐标为(Iisx,Iisy);其终点记作Iie,坐标为(Iies,Iiey),W=o∪I表示所有任务位置和所有AGV停靠点的位置集合。
由于有多个AGV 协同完成任务,所以先要将任务列表I的任务进行均衡分配,保证每个AGV 任务负载相对均衡,然后根据任务分配的结果每个AGV 进行路径规划完成任务,路径规划的原则为在尽量避免碰撞的情况下缩短任务路径。如果单个AGV 被分配到多个任务,也要在路径规划之前,确定执行任务的先后顺序。AGV 完成任务的过程可以用pick up and delivery来概括,首先前往任务起点完成pick up(取货),接着前往任务终点送货(delivery),当货物送至终点任务完成。当AGV 完成被分配的任务后会暂时处于空闲状态,等待任务列表I更新加入新的任务。为了兼顾各个AGV 任务负载均衡和利用效率,任务列表I中的新任务会按先完成先分配和轮流分配组合规则来进行分配。当新任务产生时,分配给处于空闲状态的AGV;当存在多个空闲AGV 时,优先分配给已完成任务数量较少的AGV。如此循环往复直到所有任务都被分配、AGV 完成被分配的任务,本轮作业结束。多AGV调度的流程如图1所示。

图1 多AGV调度流程示意图
为了方便建模,本文对多AGV 调度问题做出如下假设:
(1)假设每台AGV 在调度过程中都电量充足,不会因缺电停止工作。
(2)每台AGV 在调度过程中保持匀速,速度为1 个单位长度/秒,不考虑起步的加速和停靠过程中的减速。
(3)每台AGV 调度中装卸物料的时间与调度时间相比忽略不计,不影响本文问题的解决,因此本文研究的问题不需要考虑装载和卸载的时间。
(4)AGV 都是同质的,即所有硬件条件完全相同。
(5)车间的AGV 通道为横纵向布置,AGV行驶距离用曼哈顿距离表示。
1.2 数学模型
为建立多AGV 调度数学模型,定义如下模型参数、决策变量、目标函数和约束条件。
(1)模型参数。
:表示第k辆AGV 从任务i起点到任务i终点搬运物料所用的时间;
:表示第k辆AGV 从任务i终点到下一任务j起点的运行时间;
:表示第k辆AGV 从停靠点ok行驶到第一个任务起点所用的时间;
Vk:表示第k辆AGV的运行速度。
(2)决策变量。
:0-1 变量,若第k辆AGV 完成任务i后接着完成任务j,等于1,否则为0;
:0-1 变量,如果任务i被第k辆AGV 完成,则等于1,否则等于0;
:整数变量,表示第k辆AGV 完成任务i接着再完成任务j,即完成其被分配任务的先后顺序;
Smax:整数变量,表示所有AGV 完成所有任务的过程中所行驶的最长路程;
Fki:整数变量,表示第k辆AGV 完成任务i过程中的冲突次数。
(3)目标函数。
式(1)表示最小化最长路程,式(2)表示最小化AGV冲突次数。
(4)约束条件。
约束(4)保证第k辆AGV 从停靠点ok出发完成任务。约束(5)、(6)表示每个任务只会被每辆AGV完成一次。约束(7)表示所有任务都会被完成。约束(8)为线路平衡约束,用于均衡AGV任务分配。约束(9)表示AGV与任务之间的分配关系。约束(10)表示第k辆AGV 从停靠点出发到第一个任务起点间的距离时间关系。约束(11)表示第k辆AGV 完成任务i运行过程中的距离时间关系。约束(12)表示第k辆AGV 从任务i终点到下一个任务j起点运行过程中的距离时间关系。约束(13)为消除子循环约束。
2 算法设计
Double DQN 作为DQN 算法的改进,很大程度上缓解了传统DQN 中Q 值估计过度的问题,具有稳定性好、误差较小、易于实现等特点。算法的主要步骤为状态动作空间设计、奖励函数设计、神经网络训练。
2.1 状态动作空间设计
2.1.1 状态空间设计
(1)AGV状态。
表示第k辆AGV 的运行状态,停止状态用0 表示,运行状态用1 表示,碰撞状态用2 表示。
表示第k辆AGV 的实时位置,第k辆AGV 会在的区域内运行,第k辆AGV的实时位置坐标会连续变化,第k辆AGV 的实时坐标可以用来判断第k辆AGV是否顺利完成了避障以及是否完成了目标。
表示第k辆AGV 的实时目标位置,指第k辆AGV 当前要到达的目标位置(任务起点或终点)。
(2)任务状态。
I表示当前动态待完成任务列表。
表示任务i的状态。任务未分配状态用0表示,当任务i刚产生时,处于未分配状态;已分配待开始状态用1 表示,当任务i被分配给第k辆AGV 但AGV 尚未到达任务起点时,处于已分配待开始状态;任务进行中状态用2表示,
当AGV 到达任务i起点提取到物料时,任务状态转变为进行中;任务已完成状态用3 表示,当AGV 到达任务i终点卸下物料时,任务状态变为已完成,任务i被从I中剔除。
2.1.2 动作空间设计
在多AGV 调度的过程中,每个AGV 有5 个动作,分别为0(静止)、1(向上)、2(向右)、3(向下)、4(向左),每个AGV 的动作选择ak构成了多AGV 调度优化算法的动作空间A,如式(14)、(15)所示。
2.2 奖励函数设计
本文根据目标函数将奖励函数分为两个部分:目标奖励和避障奖励。每个AGV 每到达一个目标点获得的奖励为1,每个AGV 每发生一次冲突获得的奖励为-1,以每个AGV 每完成一个任务为一个迭代,每个迭代的总奖励为目标奖励和避障奖励之和,每个迭代的奖励累加为总奖励。
2.3 神经网络设计
Double DQN 算法有当前Q 网络和目标Q 网络两个神经网络,输出分别记为Qn(si,ai,θ)和Qt(s'i,aimax,θ-),其中θ为神经网络参数,随着训练的持续不断更新。本文采用有两个隐藏层的全连接结构来构建两个神经网络,损失函数为两个神经网络输出Q值的均方误差φ,如式(16)所示,其中N为目标网络更新频率。
与传统Double DQN 算法不同,本文所提出的Double DQN 重点关注经验中已经选择过的动作,只更新已选择动作的Q值,从而加快算法迭代,具体见如下算法流程。
改进Double DQN算法:车间多AGV调度优化算法
输入:状态信息(每台AGV 状态信息、任务信息)、车间环境地图Map
输出:最大Q值、每台AGV 动作选择、每台AGV目标位置
初始化:探索率ε、学习率α、奖励衰减因子γ、初始状态s0、经验池memory、目标网络更新频率C
0 for episode
1 读取车间环境地图Map 数据以及当前状态信息,根据组合规则得出每台AGV 任务分配与任务排序结果和目标位置。
2 根据每台AGV 当前观测内容选择每台AGV 动作并记录当前训练步数step。
3 for eachA∈a
4 if random(0,1)<ε
5=max(A)
6 else
7=random(A)
8 ifε_increment is not None elseε_max
//随着训练的持续逐渐增加ε到最大值
9 endif
10 endfor
11s'=s+
//将采用的动作作用于环境并计算出每台AGV的总奖励以及采取动作后的新状态s'
12
//将计算的结果存入经验池中
13 if(step>200)and(step%5==0):
//达到指定条件后开始训练
14 learn(step)
//在经验池中选取经验开始训练
15Qt(s,a)=Qn(s,a)
//当前Q网络对当前所有状态动作对的Q值估计复制给目标Q网络
16 根据采集到的经验,修改目标Q 网络输出的Q值,将之前经验中选择的动作a的Q值修改为Rtotal+γ*maxQt(s'),计算Qt'(s,a)与Qn(s,a)的均方误差,作为损失函数反向传递给神经网络进行训练。
17 以目标网络更新频率C更新目标Q 网络参数
18 endif
19s=s'//更新状态
20 step++
21 判断训练是否继续:到达终止状态(所有AGV 完成所有任务)或达到迭代次数
22 如果达到终止条件,则终止;否则从第1步开始继续训练。
23 endfor
3 算法实施与结果分析
3.1 算法训练过程
仿真训练场景设置50*50的栅格地图,经过测试,约训练4000 个回合达到收敛,故设置训练次数为4000,学习率为2e-2,设置探索概率ε由0.05逐渐衰减为0.03,采样容量大小为1000。
图2和图3 分别展示了训练过程中损失函数和奖励函数的变化情况。

图2 训练过程中奖励函数变化情况

图3 训练过程中损失函数变化情况
可以看出训练4000个回合后算法基本收敛,由图2可以看出在训练早期,由于没有训练出有效的策略,所获得的奖励较低且不稳定,随着训练的持续,智能体逐渐学习到有效策略,算法收敛。
3.2 算法性能对比
为充分展示算法性能,基于最长路程和总冲突次数两个指标,选择了不同规模的应用场景。栅格地图大小设置为50*50,AGV数量设置为5,动态任务序列长度m和总任务数量n分别设置为不同的5 组值,即5 个任务场景。结果见表1,无论哪种场景,基于改进Double DQN 的调度算法的性能表现均优于目前车间常用的传统算法(遗传算法,GA),随着任务数量的不断增加,基于改进Double DQN 的调度算法的性能优势越来越显著,最长路程最多减少18.61%,冲突次数最多减少18.58%,通过减小行驶路径长度、碰撞次数实现了节能。
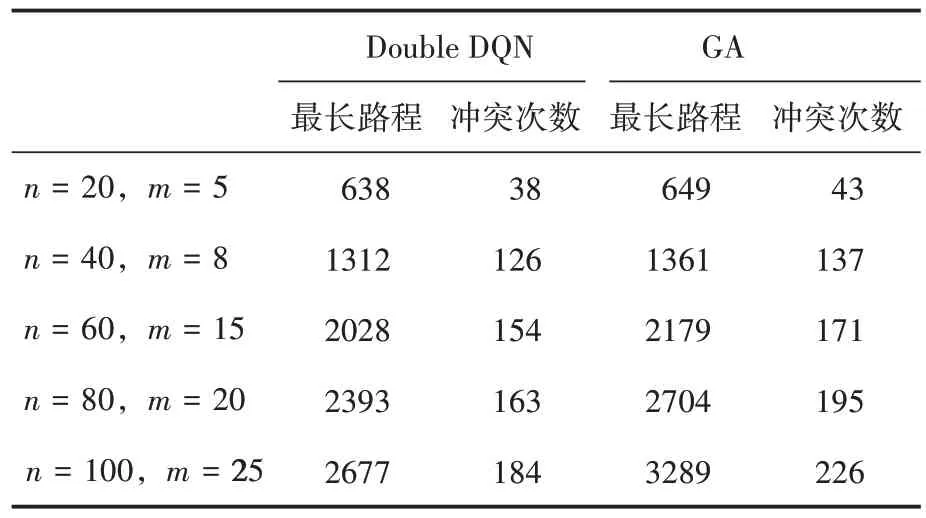
表1 算法性能对比
4 结语
本文针对当前汽车零件生产车间AGV 调度算法性能落后、忽视任务分配与路径规划耦合性的问题,应用栅格地图对多AGV 调度场景进行建模并提出了一种基于改进Double DQN 的AGV 调度算法,通过算法训练和与传统调度算法进行对比,证明了所提出算法的可行性以及在节能上的优越性。

