未知环境下基于Dueling DQN的无人机路径规划研究
赵恬恬,孔建国,梁海军,刘晨宇
(中国民用航空飞行学院空中交通管理学院,广汉 618300)
0 引言
随着大数据和人工智能技术的发展,无人机(unmanned aerial vehicle,UAV)在农业和交通等领域得到广泛应用。无人机路径规划是指在环境中规划一条安全路径,使无人机能够避开障碍物,从初始位置到达目标位置[1]。
目前,路径规划领域已经有许多研究方法可供借鉴,可以分为智能仿生学方法和传统方法两类。智能仿生学方法包括蚁群算法、粒子群算法、麻雀搜索算法等;传统方法包括模拟退火算法、人工势场法、A*算法等。Lamini等[2]在考虑距离、安全性和能源因素的情况下,提出一种基于遗传算法的路径规划方法,相较于其它算法,减少了路径步数和平均迭代次数;余翔等[3]提出改进A*算法和人工势场法的路径规划方法,通过混合式启发函数改进了A*算法的搜索节点,并与APF 算法融合,以提高路径规划的效率和摆脱局部最优点;Amala 等[4]提出了一种基于Q-Learning动态避障的无人机路径规划方法,引入最短距离优先级策略,并将其与A-star和Dijkstra等算法进行了对比,实验结果表明该方法能够减少无人机到达目标所需的距离;毛国君等[5]提出了一种改进的算法ε-Q-learning,通过不断调整贪婪因子ε,从而有效减少搜索代价。
综上所述,国内外关于无人机路径规划问题的研究相对较多且较深入。研究大多基于已知环境的信息,缺乏对未知环境信息下的三维路径规划的研究。为此,本文提出一种未知环境下基于Dueling DQN 的无人机路径规划方法,首先,在DQN 的基础上引入了对抗网络架构;其次,设计状态空间并定义离散的动作和适当的奖励函数以引导无人机学习最优路径;最后,在一定范围内随机生成的三维环境中进行仿真验证。
1 相关工作
1.1 深度强化学习
强化学习主要通过智能体与环境的交互和不断试错来学习最优策略,已广泛应用于自然科学和各种工程领域。强化学习的问题被建模为马尔可夫决策过程,其核心为四元组:{s,a,r,s'}。如图1 所示,在强化学习中,智能体负责根据环境状态s进行决策,选取动作a并执行,环境模型负责生成奖励值r和更新后的状态值,并反馈给智能体。智能体根据奖励值进行自我调整,以此不断迭代优化自身的决策机制[6]。
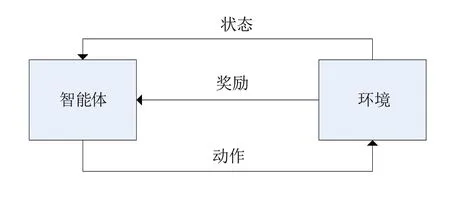
图1 智能体强化学习交互示意图
强化学习算法通常使用基于表格的Q-Learning算法。然而由于Q-table 的限制,这种算法可能无法处理高维度问题。为了解决这些问题,深度强化学习将深度学习和强化学习相结合,以解决复杂的场景问题[7]。首先,使用深度学习对输入的数据进行处理,以便发现数据中的规律。然后结合强化学习,不断调整神经网络的参数,使其能够更好地适应Q-table。最后智能体依据神经网络能够获得一个更为理想的策略[8]。
1.2 Dueling DQN算法
DQN[9]是一种强化学习算法,通过学习一个价值函数来指导智能体在环境中做出动作。然而,DQN 存在一个问题,即它将所有的动作价值都通过一个网络输出,这样会导致每个动作的价值难以准确估计[10]。因此,在DQN 的基础上引入了对抗网络架构,即Dueling DQN[11]。Dueling DQN(Dueling DeepQ-Network)是一种将神经网络分成值网络和优势网络的算法,值网络用于计算每个状态的价值函数,而优势网络用于计算每个动作相对于平均水平的优势程度,如图2所示,为DQN和Dueling DQN 的网络结构图。通过结合这两个网络,Dueling DQN 提高了算法的效率和精度,也适用于解决状态和动作空间较大的问题[12]。最终价值函数可以如式(1)所示。
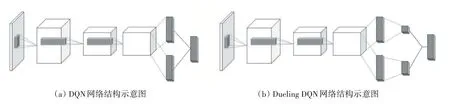
图2 网络结构图
式中:V(s,ω,α) 为状态s下的价值函数,A(s,a,ω,β)为s下采取a的优势函数,ω为网络参数;α为价值函数独有部分的网络参数,β为优势函数独有部分的网络参数。
为了对无人机当前状态进行整体评判,同时又对无人机当前状态下的动作进行优势评估,可以通过式(2)计算最终的价值函数。
式中:∑A为除当前动作a外其它所有动作的集合, |A|为动作的个数。
2 Dueling DQN在无人机路径规划中的应用
2.1 状态空间
为了保证无人机能够避免碰撞并采取合理的行动,需要考虑环境中的目标位置、边界信息以及障碍物的高度和位置[13]。在本文仿真环境中,生成多种随机障碍物,且其高度是随机变化的。通过引入这些障碍物,为无人机提供了多样化的飞行场景,增加了环境的复杂性和挑战性。这样做的目的是测试无人机路径规划算法在各种不同情况下的适应性和鲁棒性。在计算无人机当前位置与目标点位置的距离以及初始状态位置与目标点位置的距离时,使用曼哈顿距离作为衡量标准。
2.2 动作空间
动作选择是强化学习中的一个关键要素。在无人机路径规划中,无人机通过采用不同的策略来选择下一步的动作。通过执行不同的动作,无人机可以获得相应的奖励值。高奖励值表示该动作具有更高的价值,这使得无人机在下一次训练中更有可能选择该动作。通过不断优化动作选择策略,无人机可以逐渐学习到最优的路径规划策略,以获得最大的回报值[14]。在本文实验中,无人机能够采用27(所在平面网格以及上、下共三个平面的运动方向)个方向的动作,图3 所示为无人机所在平面对应的动作选择(包括静止在原地)。

图3 无人机运动方向示意图
2.3 奖惩函数
在强化学习中,奖励函数是影响无人机路径规划的重要因素,设置合理的奖励函数可以有效地提高无人机路径寻找的正确性和有效性。奖励函数R在状态S下的t时刻到t+1时刻的状态所能获得的期望奖励如式(3)所示。
累计奖励函数值Gt,也就是回报,如式(4)所示。
式中,γ是折扣因子,体现在未来时刻回报奖励的衰减效果。无人机的目标是通过找到最终目标的位置来最大化回报值。因此,奖励值的设定对路径规划的结果有不可忽视的影响。
在本文中,考虑了爬升过程中的奖励和目标奖励。爬升过程中的奖励即如果当前位置距离目标高度越远,则高度变化率对总回报造成的影响越大,如式(5)所示。目标奖励的影响受到无人机与目标点之间距离的影响。当无人机距离目标点较近时,目标奖励的影响较小;反之,影响较大,如式(6)所示。
式中,ωc是爬升参数;hz是无人机当前位置的高度;htarget是目标位置的高度;ωt是目标参数;是当前位置与目标位置的曼哈顿距离。
除此之外,奖励函数在设置的同时也考虑以下因素,如当无人机到达目标点的奖励值设置为+100,碰到障碍物的奖励值设置为-100,处于静止状态的奖励值设置为-500,步数超过最长步长的奖励值设置为-10,电量耗尽的奖励值设置为-10。
2.4 神经网络训练
Dueling DQN 的训练过程分为两个阶段:经验回放和神经网络训练。在经验回放阶段,智能体从环境中随机采样一批状态序列(s,a,r,s')并存储到一个缓存区中。这些状态序列包括成功的路径,也可以是失败的路径或任意时刻的路径。通过不断地从缓存区中随机采样状态序列,可以避免因为数据的相关性导致的数据偏差问题。如图4所示为Dueling DQN的结构图。

图4 Dueling DQN的结构图
本文采用梯度下降法来不断更新网络参数以使得训练的神经网络准确地估计Q值。为了衡量Q值估计的准确性,使用均方误差作为损失函数的计算指标。通过最小化损失函数,可以提高神经网络对Q值的准确估计能力。
3 实验结果与分析
3.1 实验场景描述
为了验证该算法的性能,本文在Python 的实验环境下对DQN 和Dueling DQN 作对比试验。首先构造了三维网格化环境,环境的长宽高均固定,分别为200、200、50,单位为米。环境中的障碍物、无人机初始状态位置和无人机目标点位置均为一定范围内的随机生成。为了减少由于无人机自身原因造成路径规划失败,在每次训练中使用10 架无人机对同一仿真实验环境进行训练。使用的激活函数为ReLU,优化器为Adam。所使用的仿真环境软硬件设置见表1。

表1 实验环境配置表
3.2 实验结果
在训练初期,无人机会以随机的轨迹前进,并且无法有效躲避障碍物,但通过学习和积累记忆,它可以逐渐学会安全地规避障碍物,并成功到达目标位置。一旦无人机在不碰撞障碍物的情况下成功到达目标位置,后续训练中它将倾向于选择这条路径作为最短路径。使用ε-greedy 探索策略,在每次训练中,无人机有一定概率按照预先设定的ε 值探索其他路径,而非仅仅选择最优路径。通过这种算法,无人机能够逐步扩充自身的经验库,并找到最优的最短路径,具体参数设置见表2。
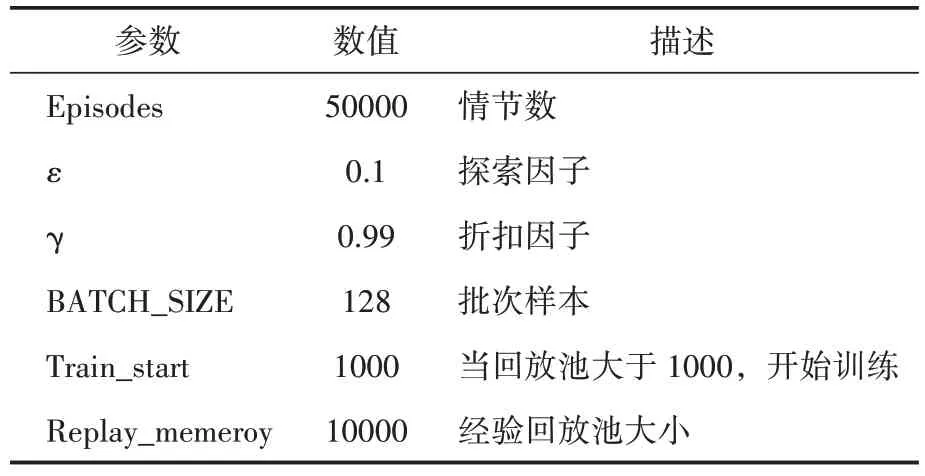
表2 参数设置
3.2.1 可视化结果对比
根据上述的实验环境和参数设置,使用DQN 和Dueling DQN同时训练50000 次,从简单环境与复杂环境进行了对比实验。实验结果如图5、图6 所示。在简单环境中, DQN 和Dueling DQN都成功地规避障碍物,找到起点到终点的路径。然而,在寻找路径过程中,Dueling DQN 不论是对障碍物的敏感度还是路径的平滑性方面都表现更好。在复杂环境下,DQN寻找出的路径在接近终点的时候陷入了局部收敛状态,而Dueling DQN 则是避开障碍物成功找到一条路径,因此,在收敛性方面Dueling DQN也优于DQN。

图5 简单环境下仿真结果示意图

图6 复杂环境下仿真结果示意图
3.2.2 平均回报值对比
图7 所示为两种算法的平均回报值对比。从图中可以看出,开始回报值为负值,表示无人机处于探索学习阶段;回报值上升表示无人机通过探索学习到了较好的策略;最后稳定阶段,表示无人机已经学习到了通往目标点的最优路径。在迭代了10000 次后,Dueling DQN 已经保持在稳定状态,而DQN 在迭代15000 次以及40000 次附近均有大幅度的变化。该结果表明基于Dueling DQN的无人机路径规划方法可规划出更优的移动路径,较高的平均回报值使无人机的方向性更好,这种方向性可以有效地避免无人机与障碍物的碰撞以及减少非必要的路径点。

图7 两种算法的平均回报值对比
3.2.3 三种指标对比
图8所示为两种算法的成功率、碰撞率和超过最长步长率对比。成功率是由在每次迭代中无人机成功找到路径的架次与总架次的比值得到的,由图8可以看出,在迭代1000次时,两种算法的成功率无很大差异,当迭代次数增加至10000 次、30000 次、50000 次时,Dueling DQN的成功率明显大幅度增加,在50000次时,保持在80.56%,而DQN的成功率仅有62.85%。

图8 两种算法对比
碰撞率是由在每次迭代中无人机因碰撞而造成该次迭代结束的架次与总架次的比值得到的,在前1000次迭代中,因为对于环境不熟悉,无人机是以一个随机的状态去选取动作,因此无法有效地躲避障碍物,在经历了10000 次与50000 次迭代后,Dueling DQN 的碰撞率也是明显低于DQN的碰撞率。
超过最长步长率是由在每次迭代中无人机因超过设置的最长步长而造成该次迭代结束的架次与总架次的比值得到的。在迭代训练的初期,无人机以随机的轨迹前进,在寻找路径的过程中会浪费大量的步数,因此两种算法的超过最长步长率均较高,随着迭代次数的增加,DQN 仅由价值函数值去选取动作,未考虑该动作的优势,因此在50000 次后,其超过最长步长率仍保持为30.68%,而Dueling DQN 由每个状态下价值函数与优势函数的数值选取最优动作,因此在50000 次后,其超过最长步长率由45.73%降至14.54%。
总的来说,基于Dueling DQN 的无人机路径规划方法相对于DQN 在未知环境下表现更好。它能够规划出更优的移动路径,具有较高的平均回报值和成功率,同时减少了碰撞和超过最长步长的概率。这意味着Dueling DQN 能够更有效地选择动作,避免与障碍物碰撞并减少不必要的路径点。因此,该方法在应急救援等复杂场景中能够高效地规划路径,避开障碍物。
4 结语
(1)基于Dueling DQN 的无人机路径规划方法在未知环境下展现出的综合性能,包括更好的收敛性、更高的成功率、更低的碰撞率以及更小的超过最长步长率。这说明基于Dueling DQN 的无人机路径规划方法在复杂未知环境下具备更强的适应性和优越性能,能够有效地应用于诸如应急救援等领域的复杂场景中。
(2)未来的研究方向包括以下几个方面:首先,进一步优化算法性能,通过改进深度强化学习的网络结构、调整超参数或引入新的训练技巧,提高路径规划算法的效率和准确性;其次在路径规划过程中考虑环境的变化,以适应实时的场景变化。这些工作将有助于推动无人机路径规划技术的发展和实际应用。

