乘法公式与几何图形

文／万广磊

学习整式的乘法公式时，大部分同学都是通过背诵来记忆公式的，很容易忘记和混淆。其实，同学们不妨选择运用数形结合的思想，结合几何图形进行理解，这样不仅能记忆清晰，还能准确应用。

在解决数学问题的过程中，人们常对同一个量（图形的面积、点的个数、三角形的内角和等）用两种不同的方法计算，从而建立相等关系，我们把这个思想称为“算两次”，也称作“富比尼原理”。这是一种重要的数学方法。接下来，我们就运用“算两次”的方法，结合长方形和正方形，来理解和记忆完全平方公式与平方差公式。

如图1，大正方形的面积可以表示成（a+b）2，也可以表示成a2+2ab+b2，于是，我们得到两数之和的平方公式（a+b）2=a2+2ab+b2；同理，如图2，我们得到两数之差的平方公式（a-b）2=a2-2ab+b2；如图3，我们得到a+b、a-b、ab之间的等量关系公式（a+b）2=（a-b）2+4ab；如图4，我们得到三个数之和的平方公式（a+b+c）2=a2+b2+c2+2ab+2ac+2bc。

图1

图2

图3

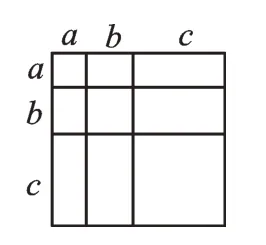
图4

同理，如图5，我们还可以得到两个数的平方差公式（a+b）（a-b）=a2-b2；如图6，我们得到两数之和的立方公式（a+b）3=a3+3a2b+3ab2+b3。

图5

图6

利用图形来记忆这些公式，你有没有觉得更简单呢？

我们再来继续研究，两个数之和的4 次方、5 次方……n次方（n≥4）的结果，有没有什么规律可循呢？对于这个问题，我们要请出“杨辉三角”了。我国南宋数学家杨辉给出了如图7 所示的三角形，这个三角形叫作“杨辉三角”，它里面的数字就是我们要找的规律。

我们把图7 中局部的汉字转化为图8 中的数字，再来研究a、b之和的乘方公式，如图9所示。

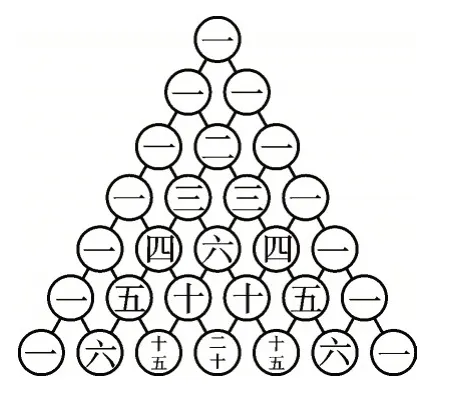
图7

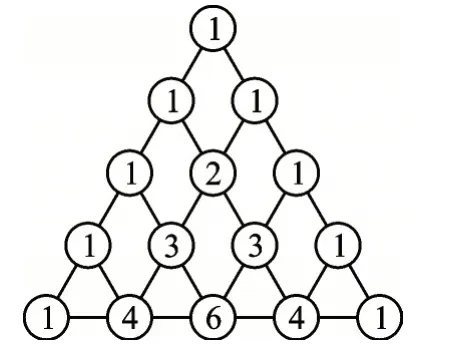
图8

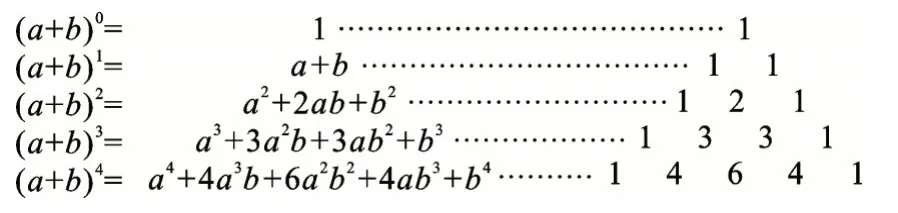
图9

如图8、图9，这个三角形给出了（a+b）n（n=0、1、2、3、4）的展开式（按a的次数由大到小顺序排列）的系数规律。例如，第三行的三个数1、2、1，恰好对应（a+b）2的展开式a2+2ab+b2中各项的系数；第五行的五个数1、4、6、4、1，恰好对应着（a+b）4的展开式a4+4a3b+6a2b2+4ab3+b4中各项的系数。没错，“杨辉三角”给出了二项和的乘方展开式中的系数规律，体现了数学的统一美、对称美、奇异美。

同学们，此时你应该会写出（a+b）5的展开式了吧？老师再来考考你们，如图10，两个两条直角边的长分别为a、b，斜边长为c的直角三角形和一个两条直角边都是c的直角三角形拼成了一个梯形。你能利用面积相等的原理，发现直角三角形的三边a、b、c之间的数量关系吗？如果能，说明你真的很棒，因为你验证了数学史上著名的勾股定理哦！

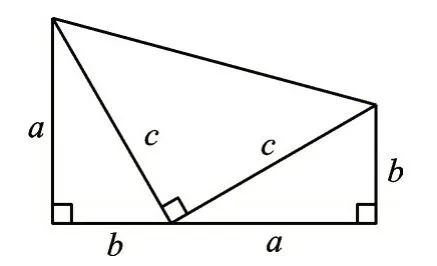
图10