多角度思考 多方法解题
文/江苏省盐城市鹿鸣路初级中学 谢天畅
苏科版数学八年级下册第73 页有这样一道题:
如图1,在▱ABCD中,对角线AC、BD相交于点O,G、H分别是OB、OD的中点,过点O的直线分别交BC、AD于点E、F。求证:四边形GEHF是平行四边形。
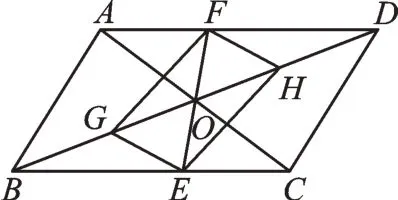
图1
要证明一个四边形是平行四边形,我们可以从平行四边形的判定方法入手。我们已经知道平行四边形的判定方法有:两组对边分别平行的四边形是平行四边形,两组对边分别相等的四边形是平行四边形,一组对边平行且相等的四边形是平行四边形,对角线互相平分的四边形是平行四边形。因此,我们可以从不同的角度进行思考,寻求解决本题的方法。
证法一:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD∥BC。
∴∠DAO=∠BCO。
又∵∠AOF=∠COE,
∴△AOF≌△COE(ASA)。
∴OE=OF。
∵G、H分别是OB、OD的中点,
∴四边形GEHF是平行四边形。
对于证法一,我根据四边形GEHF的对角线GH与四边形ABCD的对角线BD共线这一特征,选择从对角线的角度思考解题方法。
证法二:同证法一,可得AD=CB,AD∥BC,BO=DO,△AOF≌△COE。
∴AF=CE。
∴AD-AF=BC-CE,即DF=BE。
∵G、H分别是OB、OD的中点,
∴OG=OH。
∴OD+OG=BO+OH,即DG=BH。
∵AD∥BC,∴∠ADO=∠CBO。
∴△DGF≌△BHE(SAS)。
∴GF=HE。
同理,可得△DHF≌△BGE,
∴HF=GE。
∴四边形GEHF是平行四边形。
对于证法二,我找出隐藏在图形中的全等三角形,证得四边形两组对边分别相等,从而解决问题。
证法三:同证法二,可得△DGF≌△BHE,
∴GF=HE,∠DGF=∠BHE。
∴GF∥HE。
∴四边形GEHF是平行四边形。
对于证法三,我在证法二的基础上,根据图形中的全等三角形,证得四边形的一组对边平行且相等,从而解决问题。
对于此题,虽然从不同的角度出发,可以选择不同的解题方法,但是比较上面的3 种证明方法,我觉得证法一更为简捷。
教师点评
谢同学能够依据所学知识,从多个角度思考问题,积极寻求不同的解题策略,拓宽解题思路,不断发展自己的思维能力。这种勇于思考、不断探索的精神值得大家学习。

