基于套索与优化算法的矿山岩质边坡可靠度研究
郑阿鑫


摘 要:【目的】为解决拟合边坡极限状态方程时存在的过拟合与共线性等问题,且为获得更符合实际的安全系数,在考虑剪胀角的基础上,建立基于LASSO-GA-PSO的矿山岩质边坡可靠度分析模型。【方法】通过将Slide与FLAC3D相结合的方法,计算考虑剪胀角变化的边坡安全系数;采用LASSO对数据进行拟合,获得相应的极限状态方程;编写用遗传算法与LHS优化的自适应粒子群算法程序,建立基于LASSO-GA-PSO的边坡可靠度分析模型,进而确定边坡的可靠度指标。【结果】二次带交叉项的LASSO-GA-PSO模型所得的可靠度指标为2.325 7,略小于LASSO-Monte-Carlo的2.387 9,误差为2.6%。【结论】模型具有较好的优化结果,可为类似工程提供参考。
关键词:矿山岩质边坡;剪胀角;FLAC3D;LASSO算法;可靠度指标
中图分类号:TD804 文献标志码:A 文章编号:1003-5168(2024)05-0043-04
DOI:10.19968/j.cnki.hnkj.1003-5168.2024.05.009
Study on the Reliability of Mine Rock Slopes Based on Lasso and
Optimization Algorithm
ZHENG Axin
(School of Civil and Surveying Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)
Abstract: [Purposes] In order to solve the problems of overfitting and collinearity that exist in fitting the slope limit state equations, and to obtain more realistic safety factors, a mine rock slope reliability analysis model based on LASSO-GA-PSO is established based on the consideration of dilation angles.[Methods] By combining Slide with FLAC3D, the slope safety factor considering the change of dilation angle is calculated the data were fitted by LASSO to obtain the corresponding limit state equation; The adaptive particle swarm optimization algorithm program based on genetic algorithm and LHS optimization is compiled, and the slope reliability analysis model based on LASSO-GA-PSO is established to determine the reliability index of the slope. [Findings] The reliability index obtained from the LASSO-GA-PSO model of quadratic polynomial with cross terms is 2.325 7, which is slightly smaller than that of 2.387 9 of LASSO-Monte-Carlo, and the error is 2.6%. [Conclusions] The model has a good optimization result and can provide reference for similar projects.
Keywords: mine rock slope; dilation angle; FLAC3D; LASSO algorithm; reliability index
0 引言
邊坡稳定性是直接关系到矿山安全生产与发展的重大问题[1],矿山边坡滑坡等失稳状况引起的事故时有发生。例如,2023年阿拉善盟孪井滩生态移民示范区新井煤业有限公司矿区发生山体滑坡,事故最终造成较多的人员伤亡,直接经济损失达20 430.25万元。因此,合理评估矿山边坡的可靠度具有重要的理论与实际意义。
近些年,许多学者的研究极大丰富了边坡可靠度理论,常见的分析方法有蒙特卡洛模拟[2]、响应面法[3]等,亦有学者将LASSO算法应用于边坡工程中。例如,为解决响应面法的试验点选择与随机变量共线性问题,黄小城[4]将均匀设计方法与LASSO算法结合,提高了边坡可靠度计算精确度。Camilo等[5]应用LASSO算法精炼了逻辑回归模型,并分析了日本佐渡岛滑坡失效概率。谢梦龙等[6]采用LASSO算法建立了边坡土体强度参数与安全系数的关系,并通过变量筛选作用,寻找到了边坡的危险面。此外,岩土体的剪胀角Ψ也是不可忽视的参量。但传统条分法无法考虑剪胀角对边坡的影响,在实际工程中,一般假定[Ψ=0°]或φ,但均不符合实际情况[7]。
本研究从LASSO算法在边坡可靠度应用与剪胀角取值两个方面进行分析。首先,应用FLAC3D探讨边坡剪胀角对安全系数的影响,并确定Ψ的取值;其次,应用LHS进行抽样,将Slide与FLAC3D结合,计算剪胀角的安全系数;再次,用LASSO确定极限状态方程;最后,采用遗传粒子群算法确定可靠度指标,建立基于LASSO-GA-PSO的边坡可靠度分析模型,并对结果进行分析。
1 LASSO算法原理
1996年Tibshirani提出了LASSO算法(Least Absolute Shrinkage and Selection Operator),又称套索算法[8]。该算法是一种有偏估计,可以处理具有复共线性的数据,通过构造合适的罚函数,使平方误差损失最小,进而压缩高度相关变量的回归系数为零,从而获得优化回归模型。
3 工程案例
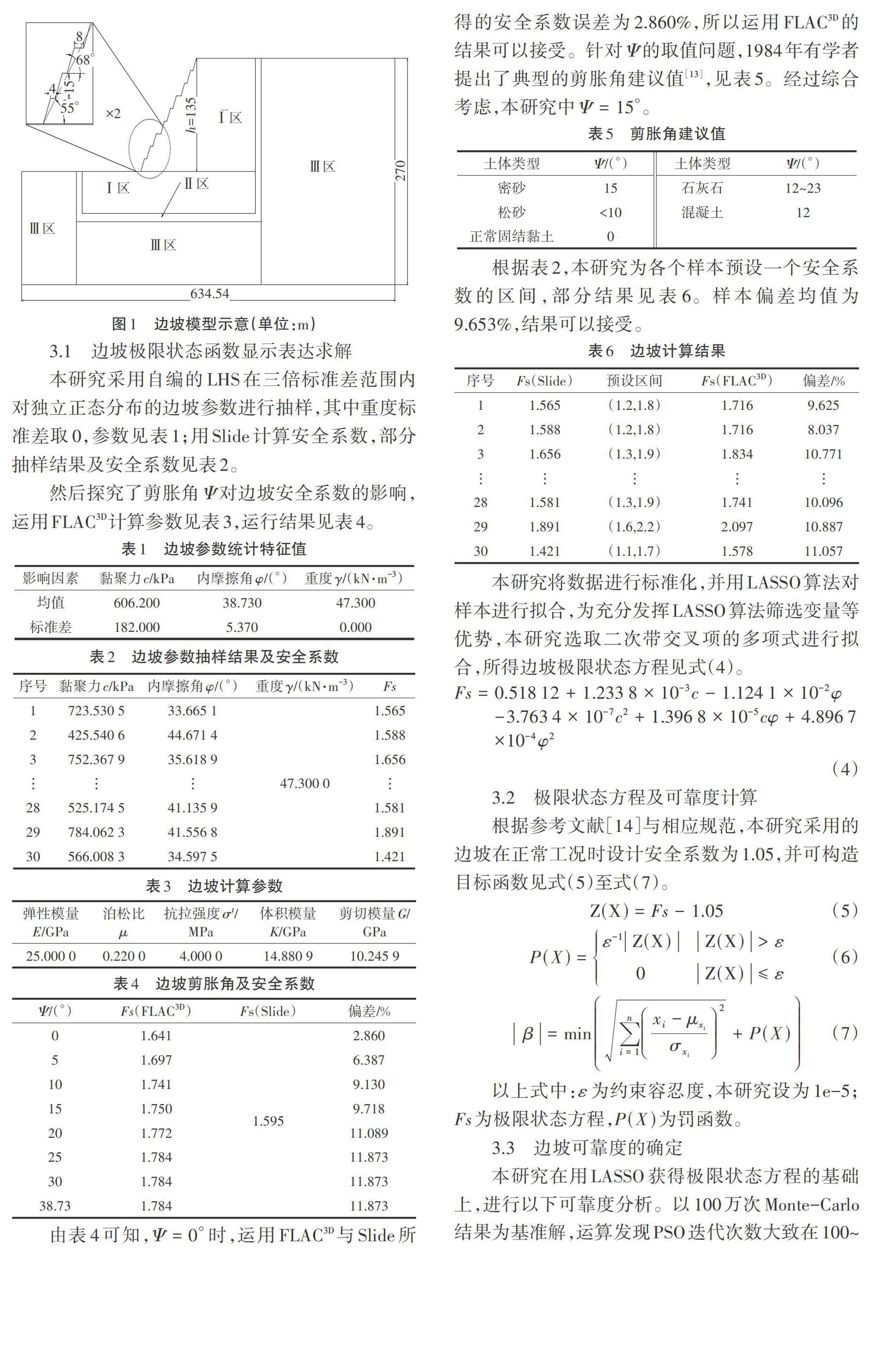
本研究以参考文献[11]中的边坡为例,根据相关研究[12],将坡顶到右边界设为2.5H,坡脚到左边界设为1.5H,高度设为2H,如图1所示。本研究将ANSYS与FLAC3D结合建模后,采用Solid 185单元将其划分成三部分:①单元约为1.0 m的加密区(Ⅰ区);②单元约为1.5 m的过渡区(Ⅱ区);③单元约为2.0 m的一般区(Ⅲ区)。
3.1 边坡极限状态函数显示表达求解
本研究采用自编的LHS在三倍标准差范围内对独立正态分布的边坡参数进行抽样,其中重度标准差取0,参数见表1;用Slide计算安全系数,部分抽样结果及安全系数见表2。
然后探究了剪胀角[Ψ]对边坡安全系数的影响,运用FLAC3D计算参数见表3,运行结果见表4。
由表4可知,[Ψ=0°]时,运用FLAC3D与Slide所得的安全系数误差为2.860%,所以运用FLAC3D的结果可以接受。针对Ψ的取值问题,1984年有学者提出了典型的剪胀角建议值[13],见表5。经过综合考虑,本研究中[Ψ=15°]。
本研究将数据进行标准化,并用LASSO算法对样本进行拟合,为充分发挥LASSO算法筛选变量等优势,本研究选取二次带交叉项的多项式进行拟合,所得边坡极限状态方程见式(4)。
3.2 极限状态方程及可靠度计算
根据参考文献[14]与相应规范,本研究采用的边坡在正常工况时设计安全系数为1.05,并可构造目标函数见式(5)至式(7)。
3.3 边坡可靠度的确定
本研究在用LASSO获得极限状态方程的基础上,进行以下可靠度分析。以100万次Monte-Carlo结果为基准解,运算发现PSO迭代次数大致在100~300之间,GA迭代次数主要为20~50,而GA-PSO迭代次数相对多一些,迭代次数主要为20~100,三类算法迭代结果对比如图2所示,结果见表7。对比可靠度指标可知,GA-PSO的结果与PSO几乎一致,与Monte-Carlo相差2.6%,而GA的结果与Monte-Carlo误差为8.8%。研究还发现GA-PSO的结果稳定,而PSO与GA存在“早熟”现象,后者更为明显,并且部分解大于GA-PSO的结果,更靠近Monte-Carlo的结果,但不符合可靠度指标几何意义。综上所述,LASSO-GA-PSO模型具有较好的边坡可靠度分析能力。
4 结论
①本研究将FLAC3D与Slide结合,考虑岩体的剪胀角Ψ,计算更符合实际的边坡安全系数,同时采用LASSO算法获得了边坡的极限状态方程,并根据可靠度指标几何意义,应用GA与LHS优化的PSO算法,计算边坡的可靠度指标,建立了效果良好的LASSO-GA-PSO矿山岩质边坡可靠度分析模型。
②本研究以某台阶边坡为例,应用LASSO-GA-PSO模型进行了可靠度分析,结果与LASSO- Monte-Carlo相差不大, 且优于LASSO-GA及LASSO-PSO的结果,该模型可为类似工程提供参考。
參考文献:
[1]杜时贵.大型露天矿山边坡稳定性等精度评价方法[J].岩石力学与工程学报,2018,37(6): 1301-1331.
[2]彭兴,李典庆,曹子君,等.基于蒙特卡洛模拟的岩质边坡可靠度设计方法[J].岩石力学与工程学报,2016,35(S2):3794-3804.
[3]李典庆,郑栋,曹子君,等.边坡可靠度分析的响应面方法比较研究[J].武汉大学学报(工学版),2017,50(1):1-17.
[4]黄小城.基于共线性问题的岩质边坡可靠度分析及其工程应用[D].重庆:重庆大学,2018.
[5]CAMILO C D, LOMBARDO L, MAI M P, et al. Handling high predictor dimensionality in slope-unit-based landslide susceptibility models through LASSO-penalized Generalized Linear Model[J]. Environmental Modelling and Software,2017,97:145-156.
[6]谢梦龙,叶新宇,张升,等. LASSO算法及其在边坡稳定性分析中的应用[J].岩土工程学报,2021,43(9):1724-1729.
[7]吴顺川,李浚弘,张化进,等.考虑岩土体剪胀特性的边坡稳定性分析[J].中国安全生产科学技术,2020,16(10):108-114.
[8]TIBSHIRANI R. Regression shrinkage and selection via the lasso: a retrospective[J]. Journal of the Royal Statistical Society. Series B (Statistical Methodology),2011,73(3) :267-288.
[9]HOLLAND J H. Adaptation in Natural and Artificial Systems [M]. Ann Arbor:University of Michigan Press,1975.
[10]KENNEDY J,EBERHART R C. Swarm Intelligence [M]. USA: Academic Press,2001.
[11]李佳伦,张志贵,李斌,等.露天矿采场边坡稳定性概率分析[J].化工矿物与加工,2022,51(9):15-18,23.
[12]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002(10):57-61,78.
[13]刘波,韩彦辉. FLAC原理实例与应用指南[M].北京: 人民交通出版社,2005.
[14]王彪龙,刘晓,郭将.基于杂交粒子群响应面的边坡稳定可靠性算法[J].人民长江,2018,49(16):97-105.

