基于ADAMS的混凝土振动搅拌机振动特性分析

孙博士,杜辉辉,周昱豪,黄益之

长安大学道路施工技术与装备教育部重点实验室,陕西 西安 710064

0 引言

混凝土是胶凝材料将骨料胶结而成的固体复合材料,是建筑工程和道路施工的主要材料,其均匀度和强度是最重要的性能评价指标[1]。在搅拌振动的过程中,对混合料施加振动,有效降低了混合料的内摩擦力和黏聚力,破坏水泥颗粒的聚集状态,加快水泥等胶凝材料的水化反应,使混凝土在宏观和微观都能快速达到均匀[2]。Lobanov et al.[3]分析了振动参数与混合料塑性黏度和剪切应力的关系,推导出振动对混合料状态的影响方程。刘慧明[4]对双卧轴振动搅拌机的振动分布情况进行研究,通过试验测试和模态分析研究振动搅拌装置的振动传播规律。王玄丰[5]发现振动搅拌过程中,不同振动参数产生的附加载荷会影响搅拌机的稳定性和可靠性。以上研究主要侧重于振动参数对混合料均匀度和设备可靠性的探讨,对振动搅拌装置振动特性的影响考虑不充分。

混凝土振动搅拌机是一种新型搅拌设备。与传统强制搅拌技术相比,采用振动与强制搅拌相结合的方式,提高了混凝土搅拌质量和效率[6]。混凝土振动搅拌机的振动特性对机器可靠性和混凝土搅拌质量有显著影响。本文结合产品实际情况,建立了单端偏心激振结构的振动搅拌装置模型,使用机械系统动力学自动分析(ADAMS)软件对不同工况下的振动搅拌模型进行仿真,研究了不同振动参数对振动系统、搅拌系统等结构振动特性的影响。最后,对仿真结果进行了对比分析,为混凝土振动搅拌机振动参数的选取提供了一定参考。

1 混凝土振动搅拌机工作原理及振动参数

1.1 搅拌机工作原理

振动搅拌机搅拌装置分为搅拌端和振动端。在搅拌端,2个搅拌轴在搅拌驱动电机的带动下同步反向运转,对拌缸内的混合料进行强制搅拌。在振动端,2个独立的振动驱动电机带动激振器与搅拌装置相连,将振动直接传递给搅拌装置。目前,混凝土振动搅拌机搅拌装置主要采用单端偏心激振结构,振动搅拌装置简图如图1所示。

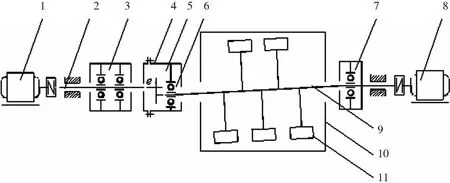
1—振动驱动电机;2—振动传动轴;3—支承轴承;4—偏心轴承座;5—激振器;6—振动端轴承;7—搅拌端轴承;8—搅拌驱动电机;9—搅拌轴;10—搅拌缸;11—拌臂及叶片。图1 振动搅拌装置简图

振动传动轴与搅拌轴连接处存在偏心轴段,搅拌轴回转轴线与振动轴回转轴线存在夹角,搅拌驱动电机带动搅拌轴围绕自身轴线做定轴转动,振动驱动电机带动振动轴高速旋转时,偏心轴段使搅拌轴绕着振动轴轴线做定轴转动。搅拌轴的整体运动可以看作一个复合运动,其振动端是类锥摆的圆周运动。在搅拌过程中,搅拌装置中的搅拌轴和拌臂及叶片时刻受到振动激励,产生振动。搅拌装置在拌缸内对混合料进行强制搅拌时,使混合料也处于颤振状态,提高了混合料搅拌效率和质量。试验证明,混凝土振动搅拌机在搅拌过程中只需达到3～5g(1g=9.8 m/s2)的振动强度,就能达到良好的搅拌效果,在确保轴承寿命和机器稳定性的同时,还能保证混凝土的搅拌质量[7]。

1.2 搅拌机振动参数

振动搅拌的主要振动参数是振动强度D、激振频率f和激振器振幅A。搅拌机的振动强度公式如下。

(1)

式中:振动传动轴驱动角频率ω=2πf是振动参数之一,激振器振幅A等于振动轴上偏心轴径的偏心距e,g为重力加速度。

理论上,混凝土进行振动搅拌时的振动强度越高,越容易破坏混合料内部的黏聚结构,缩短搅拌时间,使混合料更快达到均匀。然而振动强度过大,会导致机器本身在附加惯性力和惯性力矩的作用下,产生强烈的振动,从而降低设备的可靠性。因此,需要选择合理的振动参数,在满足机械强度设计要求的同时,为混合料提供良好的振动搅拌效果。

2 模型建立与仿真

2.1 模型建立

采用SolidWorks建模软件对单轴振动搅拌装置进行建模。本次仿真针对振动搅拌机的工作原理建立1个简化模型,在基本不减小搅拌装置刚度和质量的前提下,去掉搅拌装置不必要特征。为确保在ADAMS中,满足搅拌轴运动自由度需求,搅拌轴两端的调心滚子轴承均使用关节轴承代替。振动搅拌装置测点分布如图2所示。为研究振动搅拌系统的振动特性,在搅拌轴和振动轴上均标记5个测点,其中侧点3和侧点C分别位于振动轴与传动轴的质心处,侧点5、侧点B和侧点D位于支撑轴承质心处,侧点1位于搅拌轴振动端最大偏心距处,所有测点均布置在各轴轴线上。

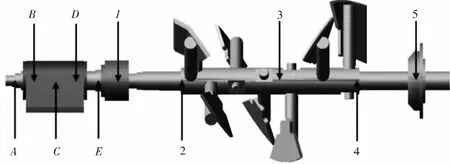
图2 振动搅拌装置测点分布图

2.2 添加约束和驱动

模型导入ADAMS后,各个零件是独立状态,需要对每个部件进行连接,组成一个机械系统。将单轴振动搅拌装置三维模型以Parasolid格式导入ADAMS中,添加各零件材料为steel,给模型添加运动副,两端关节轴承的内外圈添加球铰副。在振动轴与振动轴承座之间添加轴承模块,轴承与轴和轴承座之间的碰撞接触使用ADAMS中的冲击函数法进行模拟计算。其他部件之间均为固定副。同时为满足多自由度驱动需求,使用点驱动代替转动驱动,实现搅拌装置的振动与搅拌相结合,对振动搅拌装置同时进行运动学和动力学仿真分析。

2.3 仿真试验设计

为了研究振动参数对振动搅拌模型的振动特性影响,以偏心距e和振动频率f作为变量,进行仿真试验,仿真试验方案如表1所示。

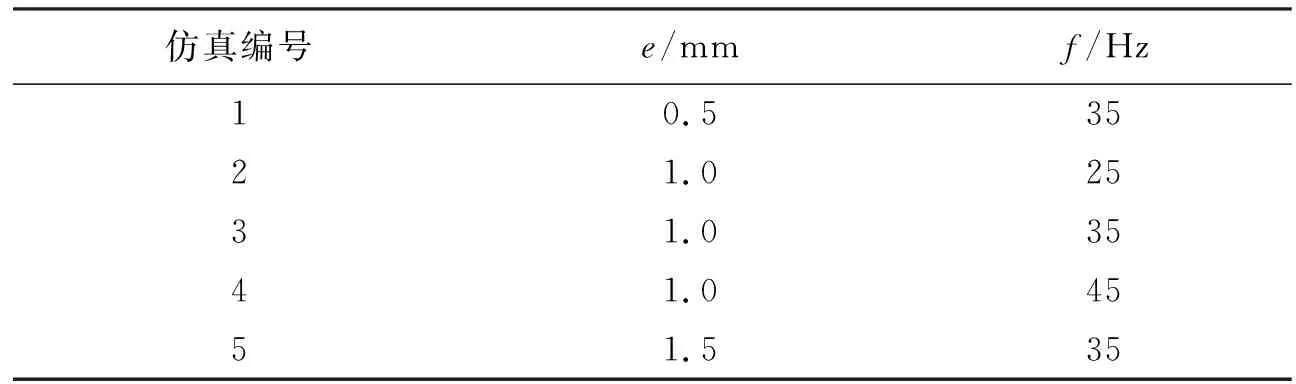
表1 仿真试验方案

3 仿真结果与分析

3.1 仿真验证分析

导入ADAMS添加运动关系,标记测点如图2所示,振动频率f为35 Hz,偏心距e为1.0 mm,设置仿真时间5 s,仿真步数5 000步。测点1的振动加速度如图3所示,因为传动轴与振动轴承座使用了ADAMS轴承模块,在启动阶段,测点振动加速度存在剧烈波动,运转稳定后,曲线为正弦波形,以搅拌轴轴向方向为z方向,则测点1在x、y方向正弦波相位差约为90°。图4是搅拌轴上各测点坐标位置随时间变化情况,在x、y方向,从搅拌轴的振动端向搅拌端,各测点振幅与各测点轴向位置为线性递减关系。由此可知搅拌轴的振动特性符合规则的圆锥振动分布。

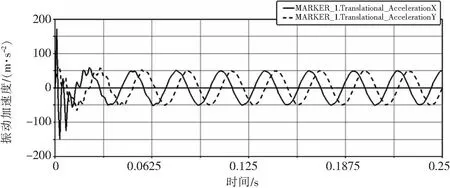
图3 测点1振动加速度在x、y方向随时间变化曲线

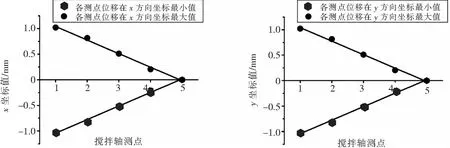
图4 搅拌轴上各测点坐标位置随时间变化情况

3.2 振动特性分析

振动参数对振动分布的影响如图5所示。

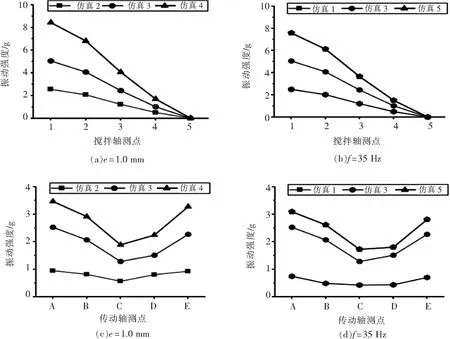
图5 振动参数对振动分布的影响

由图5(a)可以看出,在相同偏心距e下,搅拌轴上的振动强度由近振端到搅拌端呈线性衰减,即各点振动强度与振动频率成正比。由图5(b)可以看出,在相同振动频率f下,振动分布规律相似,各点振动强度的大小与偏心距e成正比。将两图进行对比分析可以看出,与最大偏心距相比,振动频率对振动强度的影响更显著。由式(1)可知,这是因为振动强度与振幅A成正比,与振动角频率ω2成正比,角频率增加1倍,振动强度则增加4倍,符合位移振动模型的振动规律。图5(c)、(d)表明在搅拌过程中,振动轴将部分振动能量通过激振器传递到振动轴上。振动轴上的振动强度由两端向中间递减,呈现“中间小,两边大”的振动分布规律。由图2可知,E点与A点相比更靠近轴承,轴承支撑力更大。而且A点远离搅拌轴振动端,受到的附加载荷更大。这使得振动轴上测点A振动强度总是略大于E,符合振动分布规律。以上仿真表明,振动参数对两轴上振动强度大小的影响较大,对两轴的振动分布规律无明显影响。

由于振动端与机架固定,考虑到传动轴的振动幅度过大时,使轴承的附加反动力过大,导致机器的稳定和可靠性差。因此,需要在增加搅拌轴振动强度的同时,尽可能降低振动轴的振动强度。从图5(c)、(d)可以看出,振动轴上振动强度受到振动频率影响更显著。因为混凝土是多相混合材料,当振动角频率ω接近或达到其共振频率时,振动搅拌效果比较理想。且需要避免激振装置的固有频率,防止振动搅拌机产生共振现象。当振动参数振动频率f为35 Hz,偏心距e为1.0 mm时,能够满足搅拌轴振动强度需求,同时振动轴振动强度较低,振动参数选择比较合理。

4 结论

1)基于振动搅拌机原理,建立了振动搅拌装置模型,满足了ADAMS中搅拌轴与传动轴的运动需求,验证了仿真模型搅拌轴的振动特性符合圆锥振动模型。

2)搅拌轴的振动强度会影响振动轴的振型,使振动轴呈现“两边大,中间小”的振动规律。搅拌轴上的每个测点符合正弦波运动规律,各测点振动加速度从近振端向搅拌端呈现线性递减规律。

3)通过仿真试验可知,振动参数对两轴上振动强度大小的影响较大,对轴上振动分布规律无明显影响。选择合理的振动参数,能够保证振动搅拌效果的同时,加强机器的稳定性和可靠性。本研究对振动搅拌装置振动参数的选取提供了参考。