从动脑思考转为动手思考的代数变形——以巧用拼图因式分解教学设计为例

赵建平 方秀娟

(1.浙江省湖州市吴兴区教育局教学研究与培训中心,浙江 湖州 313000;2.浙江省湖州市吴兴实验中学,浙江 湖州 313000)

浙教版初中数学七年级教材中的因式分解,针对十字相乘法的教学篇幅很少而且内容很浅,但高中及后续数学学习对这方面的要求却比较高.为更好掌握十字相乘法分解因式,尝试用拼图游戏的思路来设计本课,让学生在抽象的代数变形中将动脑思考转变为可操作的动手思考[1].

1 设计动脑思考解决不了的劣构问题

七年级学生对于二次项系数不是1的二次三项式还不能因式分解,教材中只对二次项系数为1的整式采用十字相乘法分解,课前设计一个学生不能解决的问题,利用“挖坑”的学习法激发学生的认知冲突,引发其动手思考.

例1 把多项式3a2+7ab+2b2因式分解.

在学生一筹莫展时,直接给出图片信息作为辅助.已有面积分别为a×a,b×b,a×b的A型、B型、C型纸片若干,拼成图形如右图所示,根据图片信息,思考能否帮助完成刚才的因式分解问题.

观察图1可以得出,长方形恰由3个A型、2个B型的正方形纸片以及7个C型的长方形纸片构成,面积即为3a2+7ab+2b2,同时长方形的面积也可以表示为(3a+b)(a+2b),即为长与宽的乘积,所以3a2+7ab+2b2=(3a+b)(a+2b).根据因式分解时定义,此即为因式分解的结果.

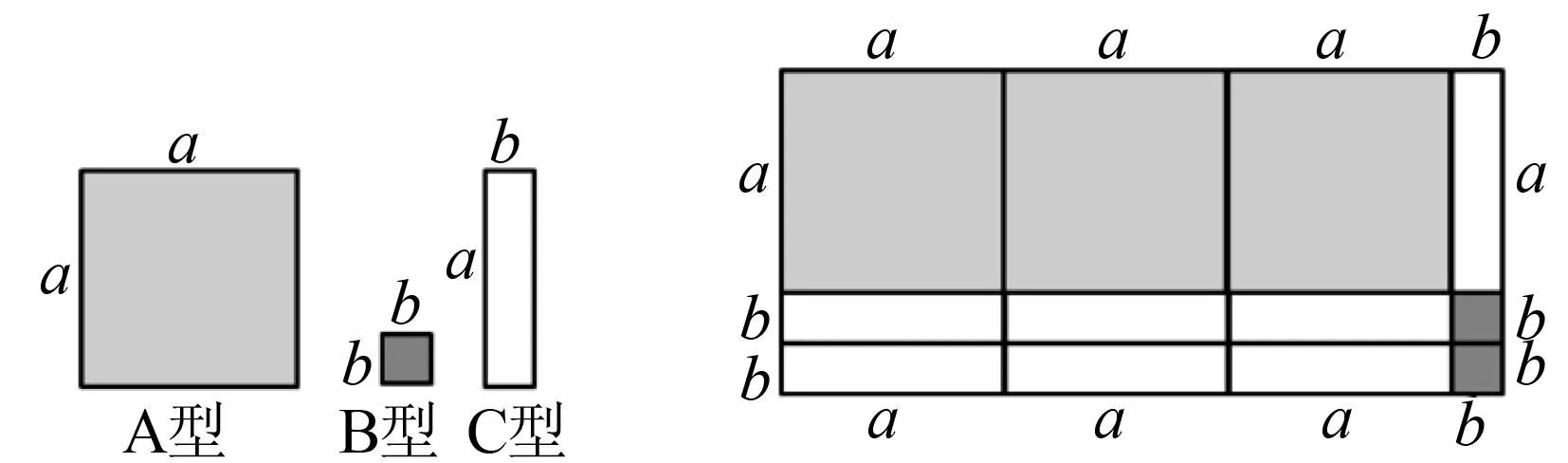
图1 A型、B型、C型纸片及其拼成的长方形

设计意图：引导学生在回忆已有的因式分解方法(提取公因式法、公式法等)的基础上,思考当遇到已有的知识不能解决的问题时如何更进一步地探究.图形信息的转换之间,可以直接读出代数语言作为结论,图形的语言信息究竟还可以有哪些规律性的结论帮助我们进行代数上的分解,触发了对以上拼图问题的进一步的思考.

2 搭建可操作性强的动手思考平台

通过有启发的尝试与探究,巧用拼图解决了较为简单的二次三项式因式分解后,通过层层推进有梯度的三个学生活动在拼图中进行技巧探寻,从而搭建了许多动手思考的平台,让学生利用提供的“支架”进行深度思考.

例2 按要求完成下列活动：

活动1：回忆完全平方公式(a+b)2=a2+2ab+b2对应的几何图形.

分析学习过程中其实已经涉及图形语言与代数信息的关联探讨.图2是边长为(a+b)的正方形,可以拆解成1个a×a,1个b×b的正方形以及2个a×b的纸片.该公式从左往右看为整式乘法,从右往左看即为因式分解,所以若能倒推先得到图形的面积构成及拼法,就能通过从外围边长反推因式分解结果.

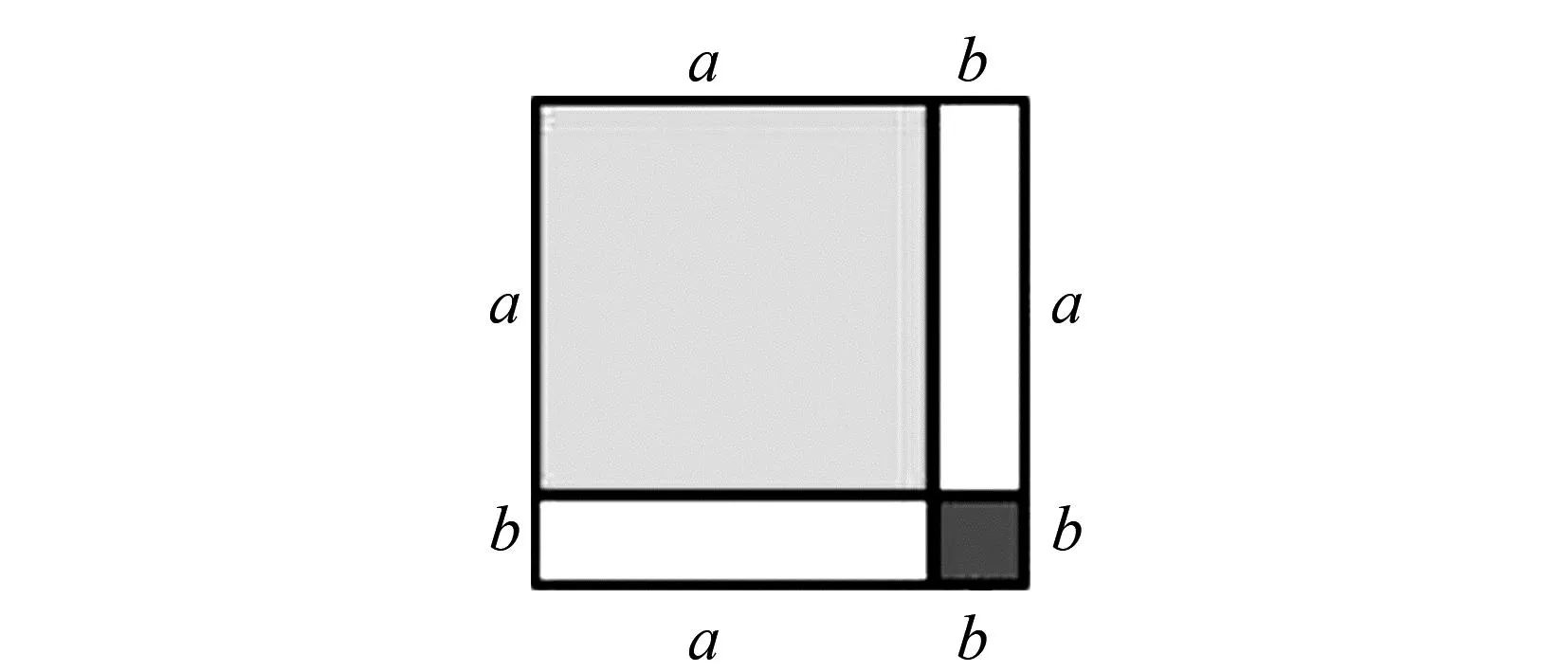
图2 (a+b)的正方形

活动2：如图3,思考1个a×a、4个b×b的正方形以及4个a×b的纸片还可以拼成怎样的规则图形,得到怎样的等式.

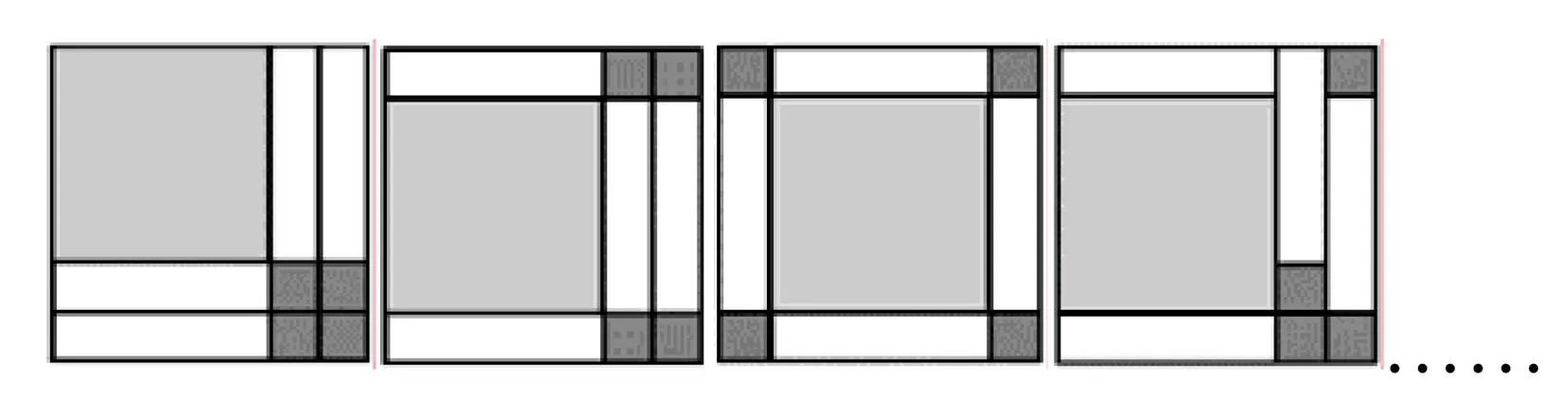
图3 不同拼图方法示意图

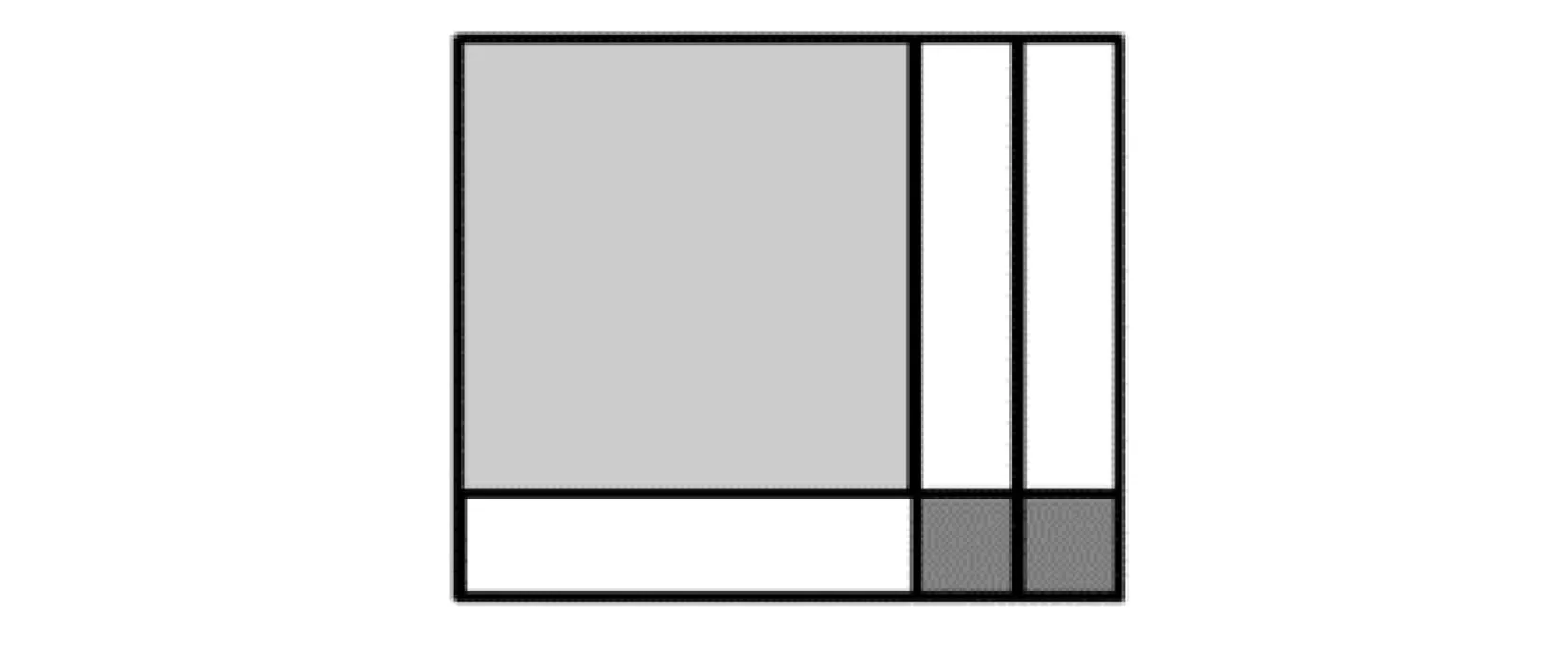
图4 活动5拼图示意图

活动3：想要拼得再大一点的正方形,至少还需要不同类型的纸片多少张,对于不同小正方形的纸片数量各有什么要求?(各类正方形纸片数量都是平方数1,4,9,……)

活动4：有3张A型(a×a),4张B型(b×b),5张C型(a×b)纸片．从中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(无空隙、无重叠地拼接),求拼成的正方形边长的最大值.

分析在得到了拼成正方形所需的小正方形数量上的规律后,范围内只有1张A型、4张C型纸片的数量是满足要求的,深化学生对于拼图过程中数量规律的理解.

活动5：分别选取适当数量的A型(a×a)、B型(b×b)、C型(a×b)纸片,拼出一个长、宽分别为(a+2b)和(a+b)的长方形,求需要A型、B型、C型纸片各自的张数,并思考如何摆放.

设计意图：从拼成正方形推广到更为普遍的长方形,一步步探究拼图过程中的数量规律(正方形数量各为平方数)和位置规律(相等边贴着放,正方形对角放,定边长再平移).基本拼图规律的总结,让之后深入运用与问题思考有迹可循.

3 拓展多维开放的动手思考空间

通过不同的动手尝试与思考,解决拼图过程的思维阻焊点.本课例中设计三个有深度问题,引发学生多角度去思考,拓展了更加开放的动手思考的空间,让学生进行从图形变化到代数变形的自我建构[2],从而利用“支架”进行深度思考.

例3 完成下列问题：

问题1：思考a2+5ab+6b2的因式分解结果.

分析1张a×a,6张b×b的正方形纸片摆放位置需要先确定,后者就有1×6,6×1,2×3,3×2几种不同位置情况,引导学生深度思考,当填补部分需要a×b的长方形个数刚好为5个时可以判断该种摆放方式符合要求.利用分类讨论的思想进行具体分析.显然,第三、四两种情况刚好满足拼图要求.此时因式分解的结果为a2+5ab+6b2=(a+3b)(a+2b)或a2+5ab+6b2=(a+2b)(a+3b).

设计意图：图5通过分类讨论面积为a2与b2的正方形的摆放位置去凑剩余部分满足中间项5ab的做法,类比于用十字相乘法因式分解中的“拆两头,凑中间”来验证的思想.

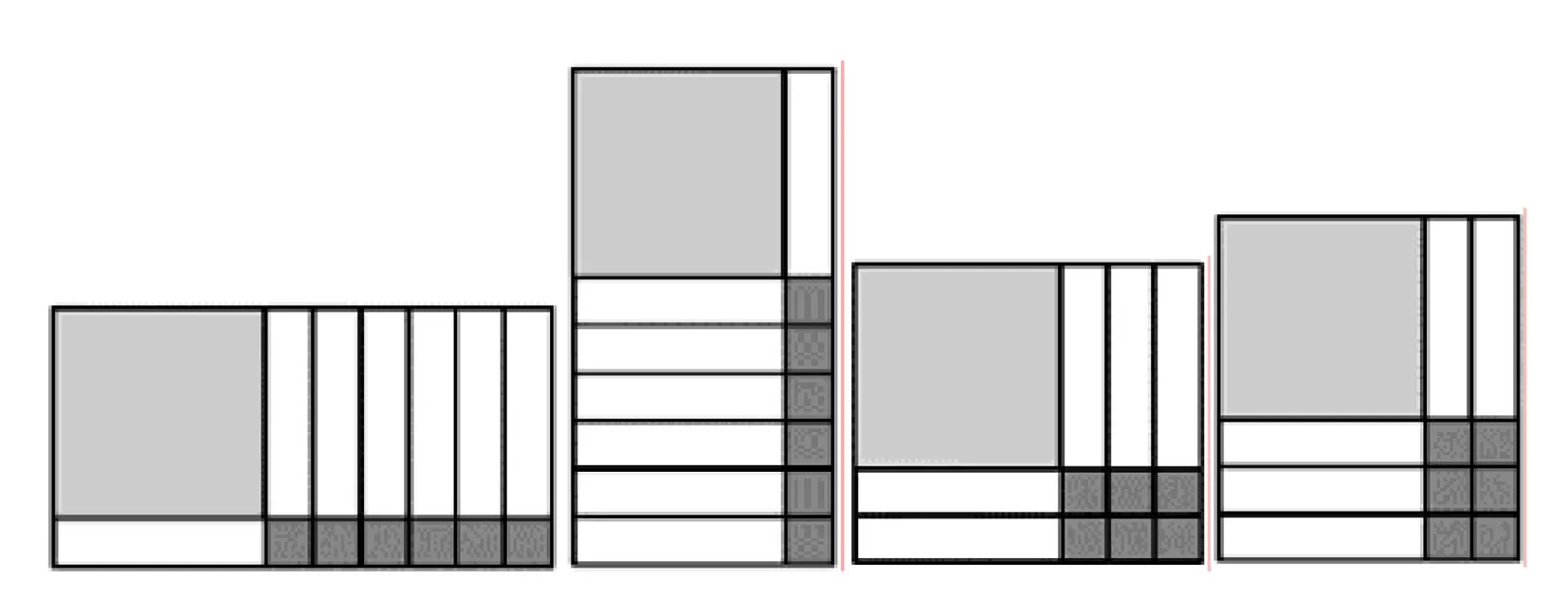
图5 问题1的不同拼图

问题2：能否用适当数量的A型、B型、C型卡片,拼成一个面积为2a2+3ab+3b2的长方形.

分析图6不论两类正方形的位置怎么摆放,所需要面积为a×b的长方形个数都不能刚好为三个,因此无法用拼图所得.

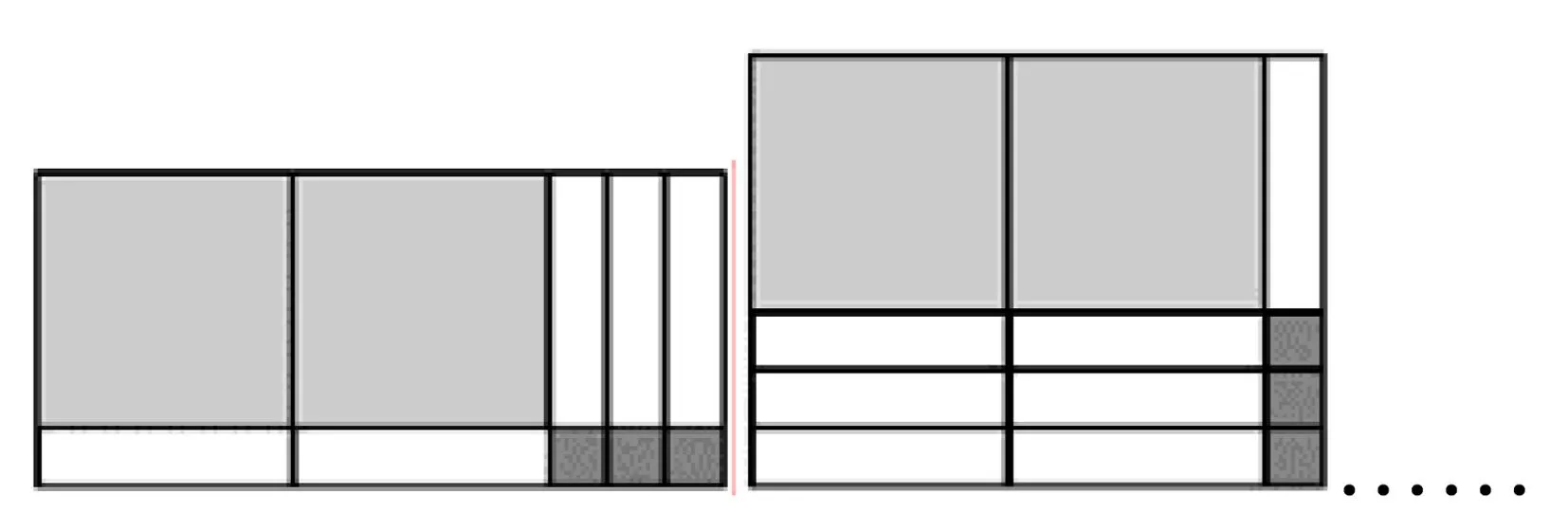
图6 问题2拼图

设计意图：若二次三项式无法进行因式分解,进而对应面积的长方形不可能通过拼图所得.发现了这一因式分解的验证依据,进一步引申对长方形面积的思考：即用来拼图的正方形与长方形纸片张数有一定的数量要求.通过问题循序渐进地抛出与解决,慢慢引导学生发现并探究拼图过程中的规律.

问题3：若取A型、B型、C型卡纸片若干张(三种纸片都要取到),拼成一个长方形,使其面积为4a2+mab+b2,求m的值．

设计意图：小组合作的形式,让学生发散性地对得到的知识进行验证与思考,在组内合作讨论、组间交流学习过程中,进一步深化对应用性知识的理解.

4 反思与建构动手思考后的活动经验

对小组合作及动手操作中积累的活动经验进行反思,提炼拼图与解决问题中的爬坑经验.本课例中的问题思考,正是反思与建构动手思考后的理论感悟,让学生在已有经验上迁移应用[3].

例4 问题思考：对下列多项式a2-ab-2b2进行因式分解.

分析回忆平方差公式(a+b)(a-b)=a2-b2对应图形的由来,如图7,若长方形的面积表达式中出现负号,巧用割补法把不规则图形通过先切割、再找等边进行拼接组成规则图形即可得到a2-ab-2b2=(a+b)(a-2b).

图7 例4拼图

设计意图：负号的引入,引发学生联想平方差公式推导过程中割补法的运用.从不规则图形转化成规则图形的化归思想,以及从遇到问题到方法找寻的思考探究过程,让学生进一步感受数学学习中数形结合、层层递进的美妙感.

5 结束语

通过先给学生设计用动脑思考无法直接解决的实际问题,激发学生认知冲突后创新,再搭建让学生操作的动手思考平台,进而逐步启发与拓展多维的动手思考空间,最后进行理论提炼后积累活动经验,从而解决生活中的实际问题.本课例通过拼图,利用给定面积的长方形的长与宽,引导学生在数形结合的思想中用拼图进行因式分解,通过“外拼”与“内割”总结不同类图形的拼接规律,巧借拼图将数学符号语言与数学图形语言进行了结合,让多维的图形变化归一成简约的代数变形表达,从而在数学动手操作中培养学生核心素养.