初中数学解题能力培养的基本策略——以人教版“圆”的相关知识为例

刘艾芳

(日照市新营中学,山东 日照 276800)

在初中数学教学中,培养学生的解题能力至关重要.笔者以具体的几何问题为例,探索培养学生数学解题能力的基本策略,旨在为初中数学解题教学提供坚实的理论和实践基础,以促进学生全面而深入地学习数学,提高学生分析问题和解决问题的能力,提升其数学核心素养[1].

1 利用基本定义和公式直接解决问题

图1 例1题图

点评本题的解决,体现了学生利用基本定义和公式直接解决问题的能力.在解决本题的过程中,学生容易发现△ABC是等腰三角形,这是根据等腰三角形的定义得出的.进一步,△ABC实际上是等边三角形,因为它的一个内角等于60°,根据等边三角形的判定即可得出结论.利用三角形的内角和定理可以计算出未知角的度数,利用圆周角定理可以推断出圆心角∠AOC的度数,这体现了学生对圆和三角形性质的基本理解[2].

2 利用辅助线解决问题

例2 如图2所示,⊙O为△ABC的外接圆,AB是⊙O的直径,作OD∥BC,与过点A的切线交于点D,连接DC并延长,交AB的延长线于点E.求证：DE是⊙O的切线.

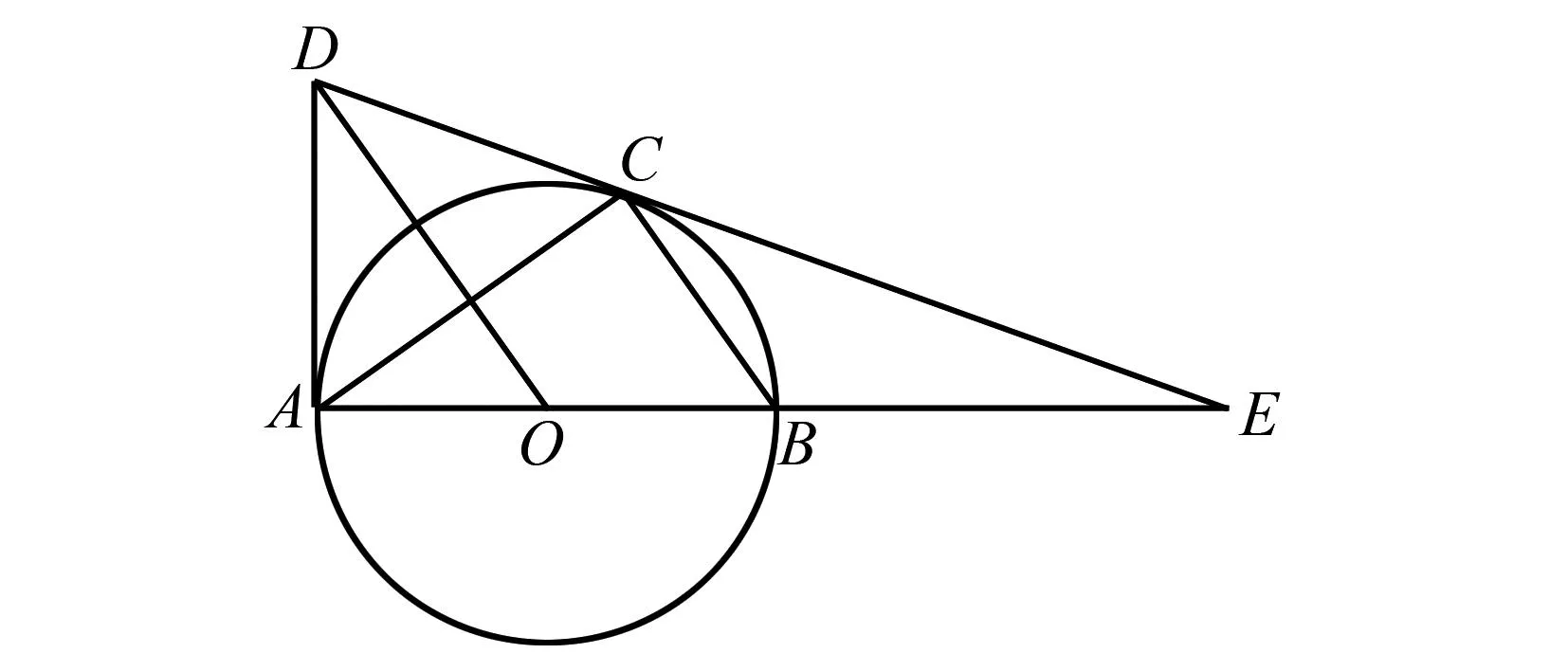
图2 例2题图

解析如图3,连接OC.因为AD为⊙O的切线,所以∠DAO=90°.因为OC和OB均为⊙O的半径,所以OB=OC,AO=CO,所以⊙OCB为等腰三角形,所以∠OCB=∠OBC.因为OD//BC,所以∠OBC=∠DOA,∠OCB=∠DOC,所以∠DOC=∠DOA,所以△ADO≌△CDO,所以∠DAO=∠DCO=90°.因为OC为⊙O的半径,所以DE是⊙O的切线.

图3 例2解法图

点评在这个问题中,引入辅助线OC是关键步骤.它建立起了已知条件与所证结论之间的逻辑关系,从而使问题得以解决.问题中运用了圆的半径相等、切线与半径垂直、等腰三角形两底角相等基本几何性质,这些都是初中数学的核心知识点,通过实际问题的解决,加深了对这些性质的理解.通过这个例子,可以使学生了解如何在解决几何问题时灵活运用基本定理和性质,鼓励学生在遇到难题时尝试引入辅助线,为问题解决创造条件[3].

3 利用转化思想解决问题

例3 如图4,水平放置的圆柱形水管道的截面半径是0.8 m,其中水面高0.4 m,求截面上有水部分的面积(结果保留π).

图4 例3题图

图5 例3解法图

点评在解题过程中,展现了转化思想的巧妙运用,将复杂的弓形面积问题转化为扇形面积与三角形面积之差,彰显了将问题转化为更简单形式的策略,为培养学生解决问题能力提供了有力的范例.

这种方法为教学实践中培养学生解题能力、数学思维能力提供了有益的经验,也适用于初中数学其他类型的题目.例如,复杂图形面积的计算问题,在计算由不同形状图形组合而成的复杂图形的总面积时,可将复杂图形拆分为三角形、矩形、梯形等基本图形,分别计算各个基本图形的面积,然后根据图形面积关系即可求得总面积.在初中数学教学中,教师可引导学生通过确定图形间的相似性或等价性,将问题转化为熟悉的图形进行求解.

4 利用发散思想解决问题

例4 已知圆O的半径是6,弦AB=10,弦CD=8,且AB∥CD,求AB与CD之间的距离d.

解析此题分两种情况讨论.

点评在数学解题教学中,分类讨论思想是一个非常重要的解题策略,它对学生解题能力的培养具有深远的影响.通过解决这道与圆有关的几何问题,可以发现分类讨论思想发挥了重要作用,它防止了漏解.其实,分类讨论思想不仅适用于几何问题,还广泛应用于代数、概率、函数等多个数学领域.

5 利用数形结合思想解决问题

例5 如图6所示,在平面直角坐标系中,以(m,0)为圆心的⊙O′与x轴相交于C、D两点,与y轴相交于A、B两点,连接AC、BC.

图6 例5题图

(2)在(1)的结论下,延长EC到P点,连接PB,若PB=PE,请证明PB与⊙O′相切;

(3)如果m=1,⊙O′的半径为2,求(2)中直线PB的解析式.

(2)如图7所示,连接O′B,则∠CO′B=2∠CAB.因为PB=PE,∠PBE=∠PEB=2∠CAB=∠CO′B,所以∠PBO′=∠PBE+∠EBO′=∠CO′B+∠EBO′=90°,所以PB⊥O′B,所以PB与⊙O′相切.

图7 例5解析图

点评本题借助数形结合思想,将圆的相关知识、直线方程、三角形及数学运算相结合,涉及初中数学多方面知识,其综合性较强,具有一定的难度.在训练此类问题时,教师要运用多媒体数字化工具,将数形结合过程演示给学生,以此激发学生的学习兴趣,培养其解决问题的能力.

6 结束语

通过对与圆有关问题的深入探讨,不仅揭示了基本数学概念和解题策略的重要性,还强调了在数学教学中培养学生综合能力的必要性.这些教学方法和思维训练将为学生打下坚实的数学基础,为其未来的学习奠定基石.希望通过本文的讨论,能够为初中数学教学提供有益的参考和启发,助力学生在数学学习道路上取得更大的成就,不断提升其数学核心素养.