剪拼构造法的实践探究

朱海燕

(浙江省宁海县城关中学,浙江 宁波 315600)

三角形是初中几何中最基本的图形,全等三角形的判定与性质是解决几何问题的重要工具.本文以具体的几何问题为例,说明剪拼构造法在解题中的应用,以此培养学生的几何推理能力.

1 题目呈现

如图1,在△ABC中,AD是BC边上的中线,F是AD上一点,延长BF交AC于点E,AE=EF,求证：BF=AC.

图1 △ABC示意图 图2 倍长中线示意图

学生根据已有的经验会想到倍长中线,如图2和图3所示.倍长中线法的本质是构造全等三角形,再结合生成的等腰三角形,通过等量代换证明结论.

图3 倍长中线示意图

2 尝试剪拼构造

通过学习,学生已经掌握了全等三角形的定义,即能够完全重合的两个三角形叫作全等三角形.若将图2中的△BDF剪下来,会与△CDG重合.利用逆向思考方法,可以将图2看成是将△BDF剪拼至△CDG后生成的构造图.类似地,图3可以看成是将△ACD剪拼至△GBD构造得到.由此可以看出,可以尝试利用剪拼法构造全等三角形[1].

下面尝试对△BDF进行剪拼.剪虽易,拼却不易,拼到哪里去?怎么拼?再次观察图2,发现可以看成是以BD=CD为条件进行剪拼的.

2.1 以BD=DC为条件进行剪拼

如图4,将△BDF剪拼至△DCG,易发现CG∥AD,△AOD与△COG都是等腰三角形.故添加辅助线后可进行如下推理：过点C作CG∥AD,且CG=DF,连接DG.易得△BDF≌△DCG,所以∠BFD=∠G.因为AE=EF,CG∥AD,所以∠DAO=∠ADO=∠G=∠ACG,所以△AOD与△COG都是等腰三角形,所以OG=OC,OA=OD,所以AC=DG=BF.

图4 △BDF剪拼至△DCG示意图

如图5,将△BDF剪拼至△CDG,此法即为图2中的倍长中线构造法.

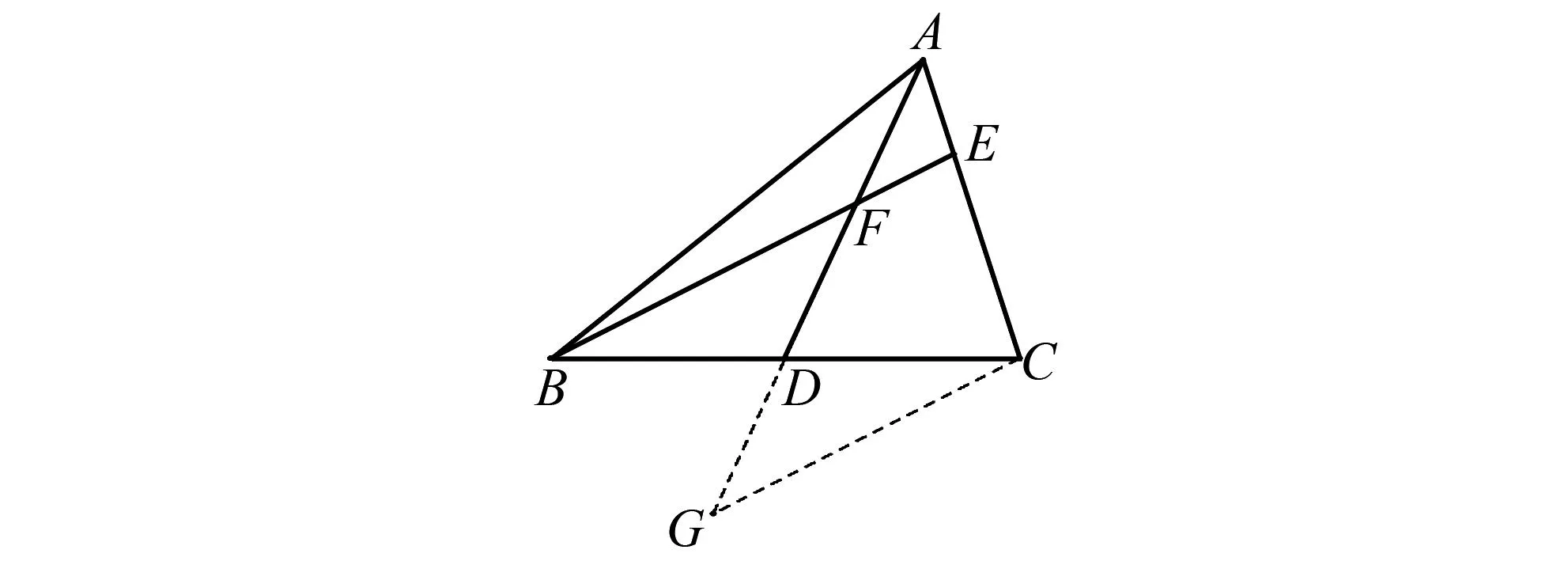
图5 △BDF剪拼至△CDG示意图

2.2 以DF=DF为条件进行剪拼

如图6,将△BDF剪拼至△GDF,生成了等腰三角形BFG和平行四边形AFGC.由此可进行如下推理：过点F作∠DFG=∠BFD,且使FG=BF,则△BFG为等腰三角形.由等腰三角形性质可得BH=GH.又因为BD=CD,所以DH是△BGC的中位线,所以DH∥GC.又易证AC∥FG,所以四边形ACGF是平行四边形,所以AC=FG=FB.

图6 △BDF剪拼至△GDF示意图

如图7,将△BDF剪拼至△GFD,生成平行四边形BDGF、等腰△AOD及等腰△COG,图形结构与图4相同,证法类似,不再赘述.

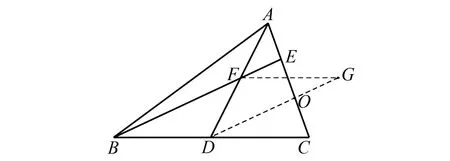
图7 △BDF剪拼至△GFD示意图

2.3 以BF=AC为条件进行剪拼

如图8,将△BDF剪拼至△CGA,生成等腰△DCG.故添加适当的辅助线后可得如下推理：过点C作CG=CD,交AD于点G,则∠FDC=∠DGC.又因为∠FAE=∠BFD,所以∠ACG=∠FBD.因为BD=CD,CD=CG,所以CG=BD,故可证△BDF≌△CGA,所以BF=AC.

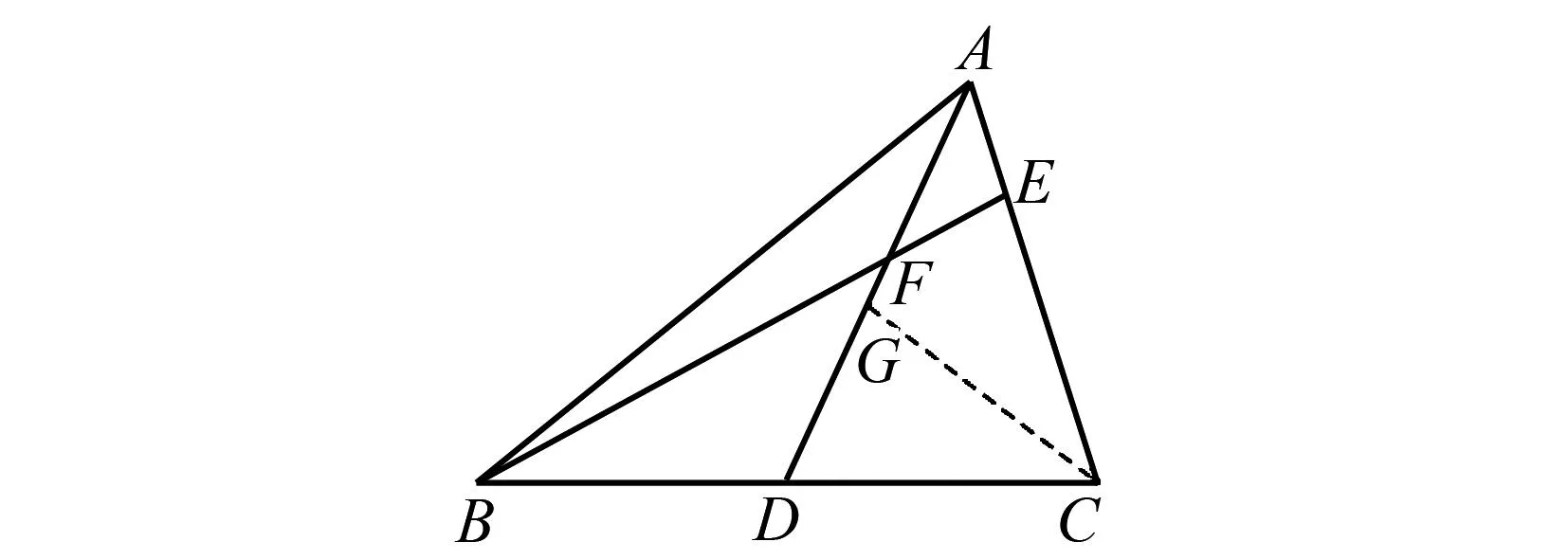
图8 △BDF剪拼至△CGA示意图

如图9,将△BDF剪拼至△AGC,生成等腰梯形ADCG.证明过程从略,请读者自行探究.

图9 △BDF剪拼至△AGC示意图

如图10,将△BDF剪拼至△CGA,生成A、D、C、G四点共圆的结构.推理过程如下：过点C作射线CG使∠ACG=∠FBD.过点A作射线AG使∠CAG=∠DAC,交于点G.通过计算法可证得∠DAG+∠DCG=180°,则点A、D、C、G四点共圆.由∠CAG=∠DAC,可得DC=CG,所以CG=BD.故△CGA≌△BDF,所以AC=BF.

图10 △BDF剪拼至△CGA示意图

由此可以看出,剪拼△BDF可以拼出7种图形,即有7种全等三角形构造法.这种剪拼方法可否应用于剪拼其他三角形?剪拼法能否作为全等三角形构造法的通法呢?为此,需对此法进行验证.

3 验证剪拼构造法

3.1 剪拼△ADC,验证构造法

3.1.1以BF=AC为条件进行剪拼

将剪下来的△ADC的边AC叠合到BF,可拼出图11、图12两种构图,其中图11生成等腰△BDG,图12生成等腰梯形BDFG.整理思路,添加适当的辅助线,推理验证易知这种构造法成立.

图11 等腰△BDG示意图 图12 等腰梯形BDFG示意图

3.1.2以BD=CD为条件进行剪拼

将剪下来的△ADC的边CD叠合到BD,可拼出图13～图15三种构图,其中图13生成等腰△BGF,图14生成两个等腰三角形,即△BOG和△DOF.图15生成B、D、F、G四点共圆的特殊结构.整理思路,添加适当的辅助线,推理验证易知这种构造法成立.

图13 等腰△BGF示意图 图14 等腰△BOG和△DOF示意图

图15 四点共圆示意图

3.2 剪拼△ABF,验证构造法

将剪下来的△ABF的边AF叠合到AF可拼出图16,其结构与图6相同,证法类似,故构法成立.

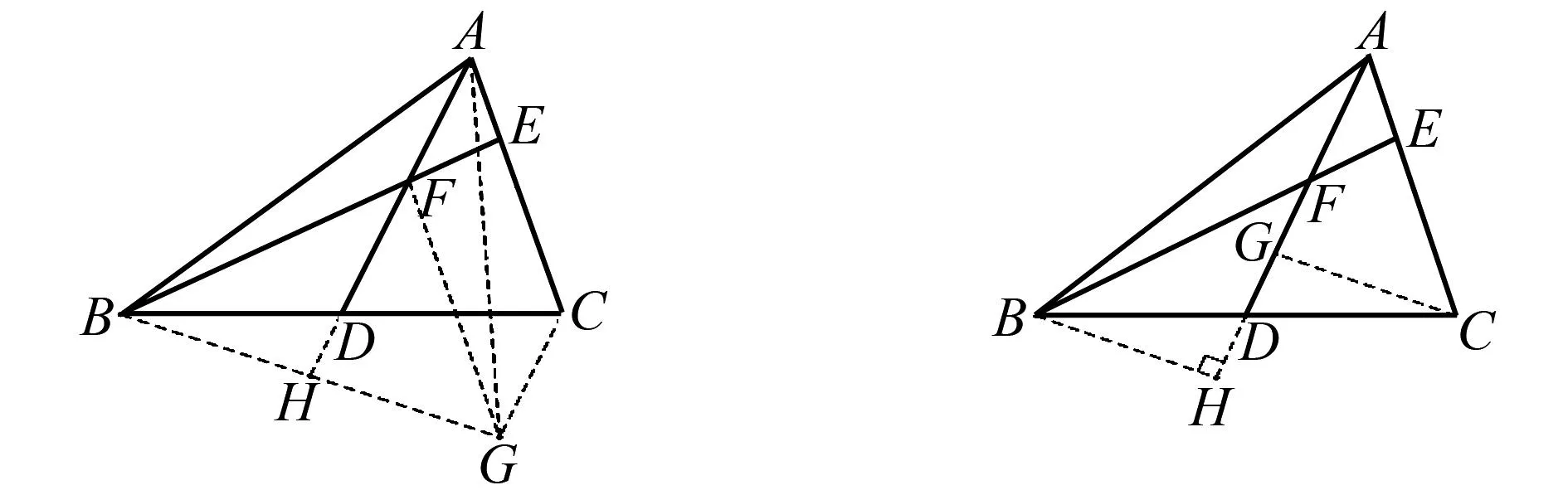
图16 剪拼△ABF示意图 图17 构造直角三角形示意图

3.3 构造直角三角形,再剪拼

除了剪拼已有三角形外,也可先构造直角三角形再剪拼.过点C作CG⊥AD,构造出Rt△ACG,再将它以AC=BF为条件进行剪拼得图17.所构图中,易证△BDH≌△CDG,得BH=CG,于是可证△ACG≌△FBH.故构法成立.

由此可见,剪拼构造法可以作为构造全等三角形的通性通法,它可以为解题助一臂之力.

4 方法归纳

4.1 剪拼构造法的解题步骤

剪拼构造法的解题步骤是：将待证线段或角所在的三角形剪下;在原图中找出与所剪三角形的边或角相等的基本元素;以线段的相等或角的相等为基本条件进行叠合拼图;观察所拼图形是否生成特殊结构,以此作为构法成立的基本依据;整理思路,添加适当的辅助线,然后进行推理论证[2].

4.2 剪拼构造法的经验总结

(1)不同的剪拼可以得到不同的拼图.通过大量的剪拼试验,笔者发现有效构图具备以下几个特点：①拼图后生成新的特殊结构,如等腰三角形、等腰梯形、平行四边形、全等三角形、四点共圆等;②拼图后能将分散的条件聚拢集中.

(2)剪拼构造法的提炼经历了“观察想象——尝试构造——构法验证——方法归纳”的探究路径,这可以成为解题方法探究的基本模式.

5 结束语

总之,在初中数学教学中,教师应该带领学生进行各种各样的实践活动,增加初中数学课堂教学的有效性.实践性的课堂教学不仅能促进学生对已学知识的深度理解,还能培养学生的探究能力,激发学生的创新思维,提高学生运用所学知识分析问题和解决问题的能力,从而培养其数学核心素养[3].