几何符号语言训练初探

耿 征

(徐州市第十三中学,江苏 徐州 221006)

《义务教育数学课程标准(2022年版)》指出,学生要会用数学的语言表达和描述现实世界.在这种理念的指导下,笔者先对两个案例进行分析,指出学生学习几何符号语言存在的困难,再针对困难从宏观和微观两个方面给出解决策略.

1 案例分析

例1 如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证：∠CFE=∠CEF.

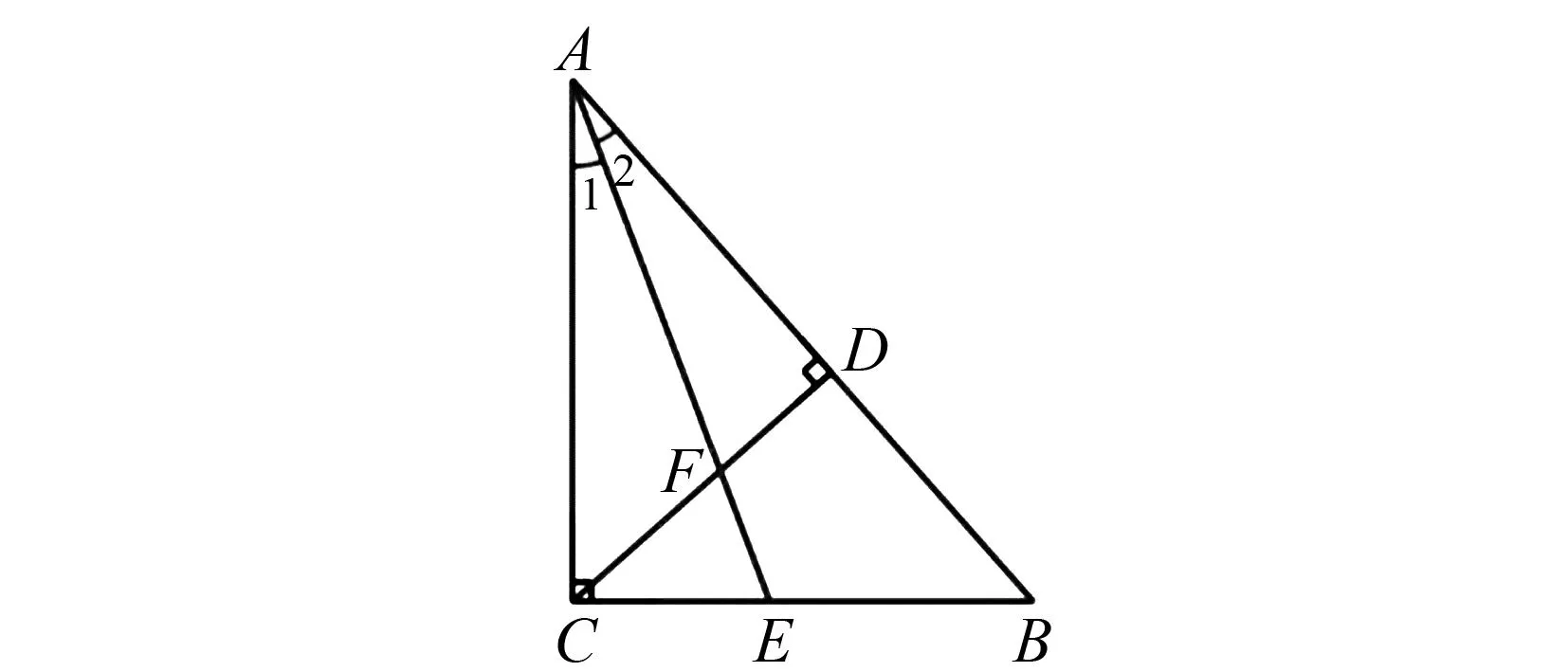
图1 例1题图

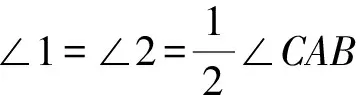
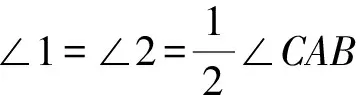
由此可以看出,在证明几何命题时,学生需根据已知条件和所证结论选择合适的几何定理作为推理的依据,并将几何定理或概念用符号语言表示出来,这是学生学习几何符号语言的第一个困难.

例2 如图2,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,连接BM,DM,MN.求证：MN⊥BD.

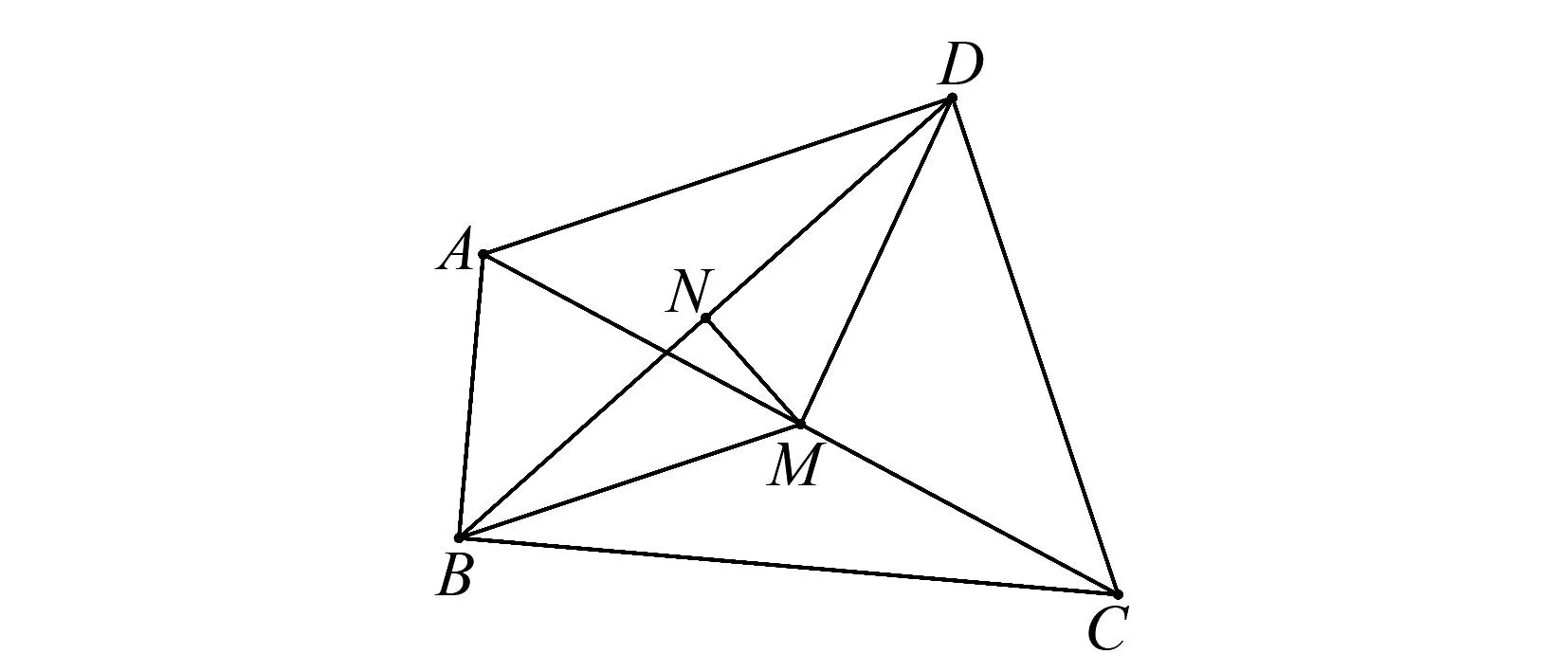
图2 例2题图

解析根据已知条件∠ABD=∠ADC=90°,易得△ABD和△ADC都是直角三角形.根据图形结构特征,BD是△ABD的斜边,AC是△ABC的斜边.又因为M、N分别是AC、BD的中点,根据直角三角形斜边上中线的性质可得BM=AM=MC,DM=AM=MC,所以BM=DM,即△BMD是等腰三角形.由等腰三角形“三线合一”性质可知MN⊥BD.

显然,本题主要考查直角三角形斜边上中线的性质和等腰三角形“三线合一”的性质,这是《义务教育数学课程标准(2022年版)》规定的最基础最核心的内容,是学生必须掌握的基础知识.从图形方面来看,本题涉及直角三角形和等腰三角形,这学生最常见的基本图形.学生见到这个图形很多遍了,但是仍然存在困难,不知道该如何下手.为什么会这样呢?笔者认为,符号语言的学习,归根结底就是对每个定理的符号语言的学习.符号语言表达能力的训练,本质上是对文字语言的理解,就是用图形和符号理解几何命题.而符号语言表达的本质,就是图形和符号的联想,即由图形想到相应的符号语言.由此可以看出,学生缺少文字语言和图形语言、符号语言之间的互相转化的能力,是几何符号语言学习的第二个困难,是影响学生几何推理能力的关键.

2 解决策略

2.1 从宏观方面而言,需建构知识体系

学生对几何图形的认识,是一个由简单到复杂的过程.先是认识点、线,再到形、体;先是每种图形的定义、表示方法,再到每种图形的性质和判定;先是孤立学习每个图形,再到图形之间的联系和结合.

2.1.1建立图形体系

对于点而言,初中阶段仅仅认识其表示方法;对于线而言,包括直线、射线和线段,根据直线的位置关系,有相交线和平行线两种,而相交线又会产生角;对于形而言,初中阶段主要研究三角形、四边形和圆三种图形,如图3所示.

图3 基本几何图形体系图

2.1.2建立图形性质和判定体系

以四边形为例,初中阶段主要从旋转角度研究特殊的四边形,包括平行四边形、矩形、菱形、正方形,而每一种图形的性质和判定研究的过程又很相似,具体见表1和图4.

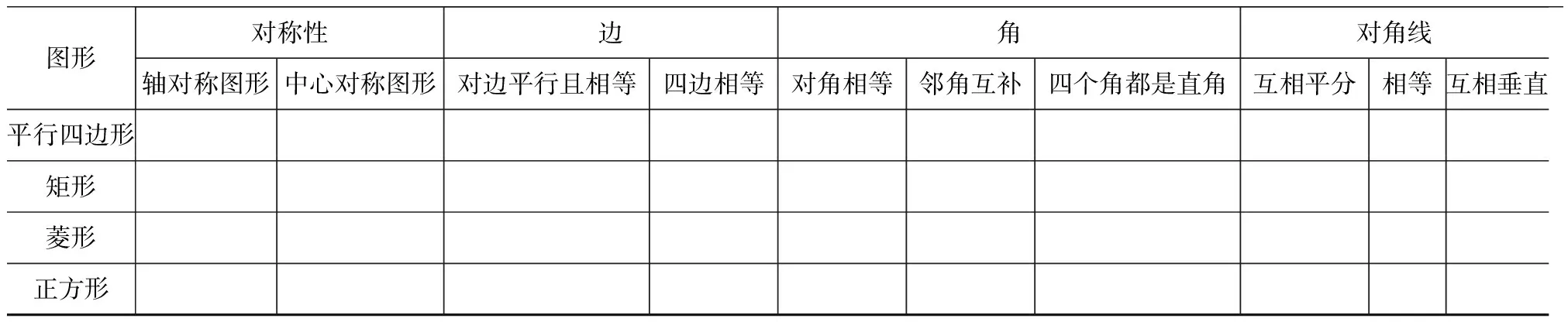
表1 特殊四边形性质判定体系表

2.2 从微观上而言,需建立不同语言相互转化的桥梁

数学语言包括文字语言、图形语言和符号语言.在初中数学学习中,所有的数学问题基本是通过这三种语言来描述的,许多数学问题的解决也是依靠数学语言之间的转换实现的[1].

2.2.1明确每个命题的本质——条件和结论

在学习“三角形内角和定理”时,教师可提出问题：你能将其改写为“如果…,那么…”的形式吗?学生思考并回答：如果一个图形是三角形,那么它的三个内角的和是180°.教师总结,此命题的条件就是“一个三角形”,结论就是“三个内角的是180°”.教师由此引导根据条件画出几何图形,并根据条件和结论,用符号语言描述这个命题,然后利用所学知识进行证明.学生完成后,教师总结,得到三角形内角和定理,如表2所示.

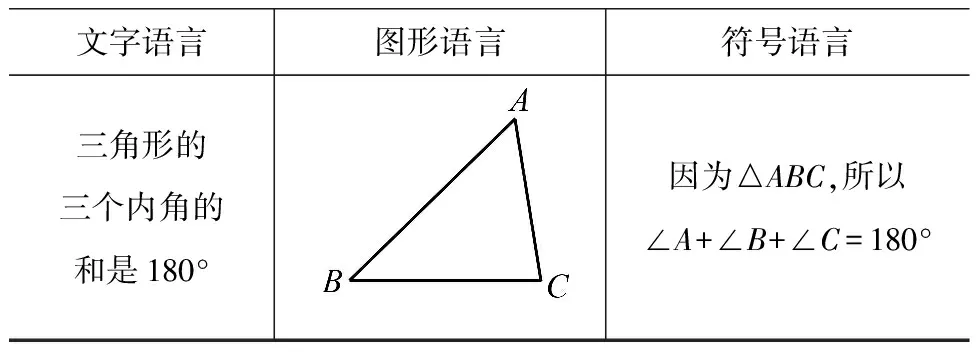
表2 三角形内角和定理三种语言表

每个命题都是由条件和结论组成的,而这也正是每个命题的本质,明确了条件和结论,学生就不会再出现条件和结论分离的情况.因此,每个命题的学习,都需先引导学生明确条件和结论.

2.2.2有意识强化三种语言之间的联系

对于每一个命题,文字语言、图形语言和符号语言是不可分割的.在初中数学教学中,教师需有意识引导学生强化三种语言之间的相互转化.

例3 如图5,在△ABC中,AC=5,BC=4,AB的垂直平分线DE分别交AB、AC于点E、D.求△BCD的周长.

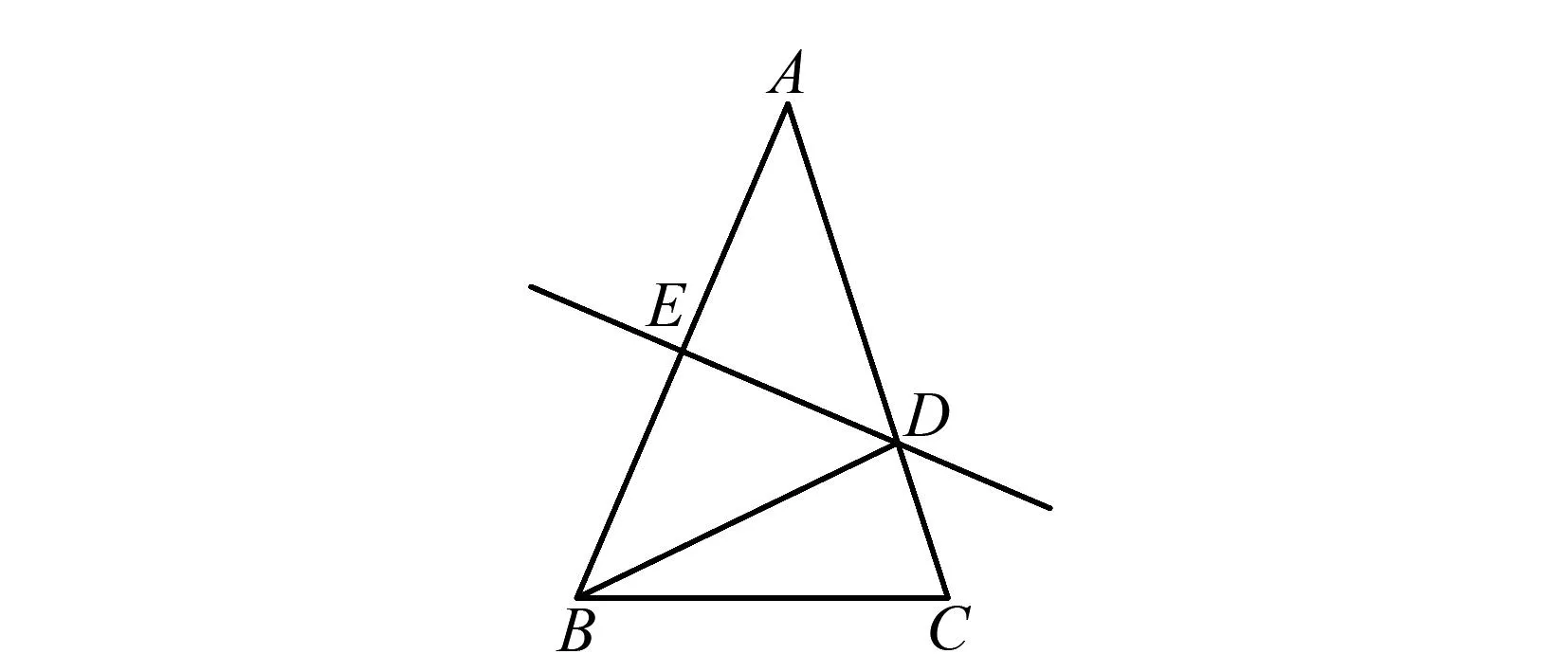
图5 例3题图

解析根据已知条件可知DE是线段AB的垂直平分线,由线段垂直平分线的性质可知DA=DB.从而△BCD的周长为BC+CD+DB=BC+CD+AD=BC+AC=9.

显然,本题主要考查线段垂直平分线的性质,即线段垂直平分线上的点到这条线段两个端点的距离相等.解决本题的关键是实现文字语言、图形语言、符号语言之间的相互转化,从而建立已知条件与所求结论之间的逻辑关系,为问题解决创造条件.在解决本题时,教师可引导学生在图5中标注已知条件中的垂直平分线,并根据垂直平分线的性质表达推理过程.即“因为ED垂直平分AB,所以DA=DB”.显然,当学生在图形中标注垂直平分线时,就自然能够写出相应的符号语言.

因此,对学生而言,每一道几何命题都是强化训练的一次机会.每遇到一个问题,教师都要引导学生借助关键词找到相应的图形.这样就能够将文字语言、图形语言和符号语言紧紧联系在一起.

3 结束语

在日常教学中,有意识地从宏观方面构建几何图形体系,从微观方面关注每个定理三种语言之间的转化,可以有效提高学生几何符号语言表达能力,从而提高学生运用所学知识分析问题和解决问题的能力,提升学生的几何推理能力.