专题教学中解题回顾的实践探索——以八年级几何教学为例

傅 鹏

(镇江市伯先中学,江苏 镇江 212132)

专题教学是一种针对特定主题进行深入学习的教学方法,与传统的零散知识点教学相比,它能够帮助学生建立知识的整体框架,提高学生的学习兴趣和主动参与度[1].目前,很多教师认为专题教学就是让学生多练习题、多接触不同的题型,因此现有的专题教学主要以题海战术为主.但在这种模式下,学生只能机械化解题,“见树木而不见森林”,不利于学生解题能力的提升.

1 解题回顾的含义

波利亚在他的著作《怎样解题》中将解题过程分为四个阶段：理解问题意思、拟订方案、执行方案和回顾.其中回顾意为检查完整的答案,重新审查结果及得出该结果的过程.解题回顾是解题过程中的重要环节,它是解题活动中的“元认知”.通过解题回顾,不仅可以发现解题活动中的问题,还可以弄清数学问题的深层结构和数学思想方法.解题回顾的目的是帮助学生深入理解解题过程,发现解题中的错误和不足之处,并从中获取反馈和改进的机会.通过回顾,学生可以审查自己的解题思路和方法是否正确,是否符合问题的要求,是否运用了适当的数学知识和技巧.解题回顾是培养学生批判性思维和自主学习能力的重要环节.通过反思和总结,学生可以不断提高自己的解题能力和数学思维水平.

在几何模块,按照图形的结构特征,可以分为不同的几何模型.学生在平时的解题过程中,主要存在着以下几个问题：一是无法精准识别几何模型,即混淆不同的图形,无法正确识别和分类不同的几何模型;二是对模型的基本结论不够熟悉,即缺乏对几何模型基本结论的了解;三是对模型的处理方法不熟悉,即学生不知道如何构造和操作几何图形,对不同几何模型的处理方法不熟悉;四是对特定模型的解题方法只知其然而不知其所以然,即学生只知道特定模型的解题方法,但缺乏对其背后原理和推理过程的理解.

2 教学实践

2.1 一题多变,融会贯通

一题多变中的“变”,意为“变式”,是指在某一特定的数学定理、模型或规律的基础上,通过改变条件、参数或数学情境,衍生出多个新的题目或问题形式.无论题目如何变化,都需要去掉题目的表面修饰,紧抓本质.通过一题多变的方式,可以深入挖掘知识的内涵和外延,帮助学生理解和掌握知识.

例1 如图1所示,∠DAE的两边上各有一点B、C,连接BC,求证：∠DBC+∠ECB=180°+∠A.

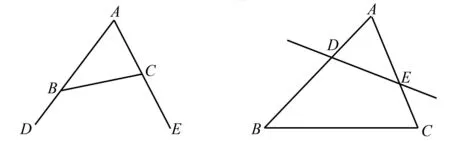
图1 例1题图 图2 变式1示意图

解析因为∠DBC和∠ECB是△ABC的外角,所以∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC.又因为∠A+∠ACB+∠ACB=180°,所以∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=180°+∠A.

点评本题主要考查三角形外角的性质,熟知三角形的外角等于与它不相邻的两个内角的和,以及三角形内角和等于180°是解题的关键.

变式1 如图2所示,△ABC中,∠A=65°,直线DE交AB于点D,交AC于点E,则∠BDE+∠CED=( )

A. 180° B.215° C. 235° D. 245°

解析因为∠A=65°,所以∠ADE+∠AED=180°-65°=115°,所以∠BDE+∠CED=360°-115°=245°,故答案为D.

点评本题主要考查三角形的内角和定理,与图1相比,图2略微复杂,但考查的知识点不变.

变式2 如图3所示,在△ABC中,∠C=70°,沿图中虚线截去∠C,则∠1+∠2=( )

图3 变式2示意图

A. 360° B. 250° C. 180° D. 140°

解析在△ABC中,因为∠C=70°,所以∠A+∠B=180°-∠C=110°,所以∠1+∠2=360°-110°=250°,故选B.

点评本题由三角形的内角和定理延伸到多边形的内角和定理.一方面,可利用三角形内角和定理求出∠A+∠B=110°;另一方面,可考虑利用四边形的内角和为360°求解.与变式1相比,本题难度更进一步.

变式3 图4是某建筑工地上的人字架,若∠1=120°,那么∠3-∠2的度数为.

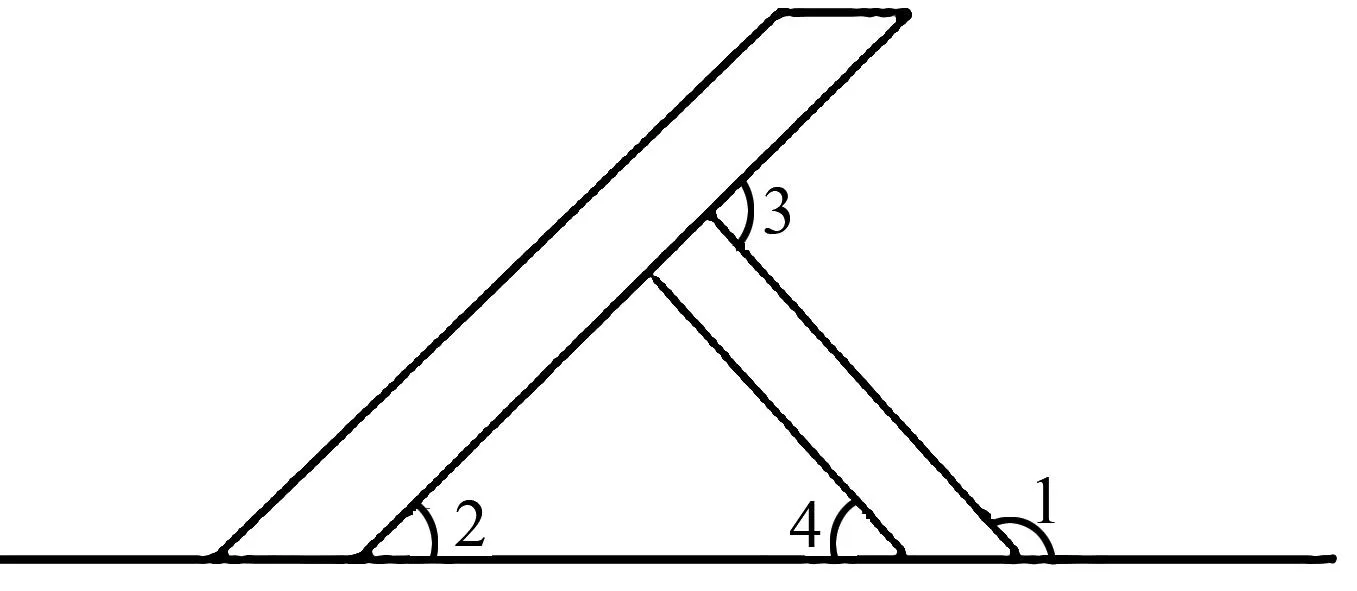
图4 变式3示意图

解析如图4,因为∠1+∠4=180°,∠1=120°,所以∠4=60°.因为∠3=∠2+∠4,所以∠3-∠2=∠4=60°.

点评本题结合实际生活情境,主要考查三角形外角的性质、平角的性质等知识,解题的关键是熟练掌握基本知识.

变式4 如图5所示,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=____．

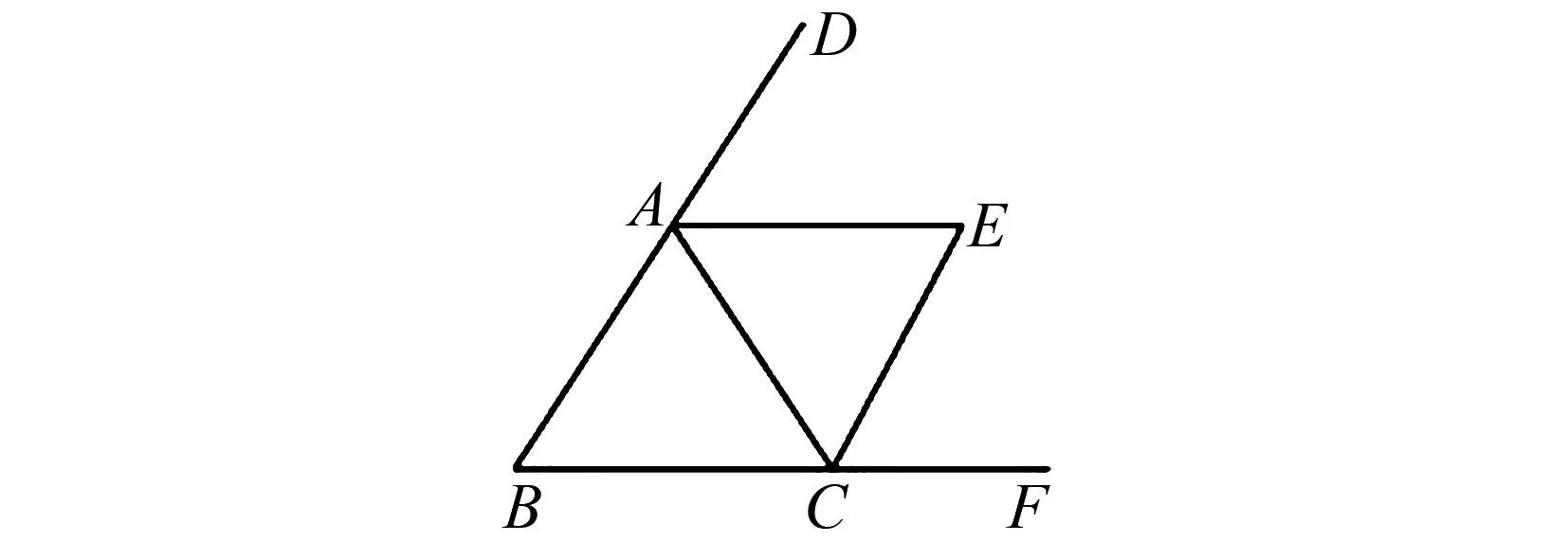
图5 变式4示意图

解析利用三角形内角和定理及角平分线的性质易得∠AEC=60°,求解过程从略.

在数学教学中,引导学生通过探索问题的变式,可以帮助学生更深入地理解数学概念和原理.例如,通过将问题的条件稍作修改,或者将问题中的一些数值进行调整,可以引导学生思考问题的本质和关键点.这种探索过程不仅可以帮助学生理解数学概念的内涵,还可以培养学生问题解决能力和创新思维.另外,数学中存在许多关联性知识,通过探索这些相关问题,也可以帮助学生加深对数学知识的理解.

2.2 一题多解,开阔思路

一题多解是指在解决一个问题时,存在多种不同的解决方法或策略.在数学的专题教学中,一题多解可以帮助学生从不同的角度去思考和解决问题,拓宽他们的思维方式和解题思路.不同的解法可以启发学生发现问题的多个解决路径,激发他们的创造力和想象力.通过比较多个解法,学生可以更深入地理解问题的本质和要求.

图6 例2题图 图7 证法1示意图

证法2 (构造梯形)如图8,作NQ∥MB交BC于点Q.证明过程从略.

图8 证法2示意图 图9 证法3示意图

证法3 (转移角构造全等三角形)如图9,作BH⊥MN于点H,连结BN.证明过程从略.

证法4 (转移角构造相似三角形)如图10,连结BN,作EN⊥MB于点E.证明过程从略.

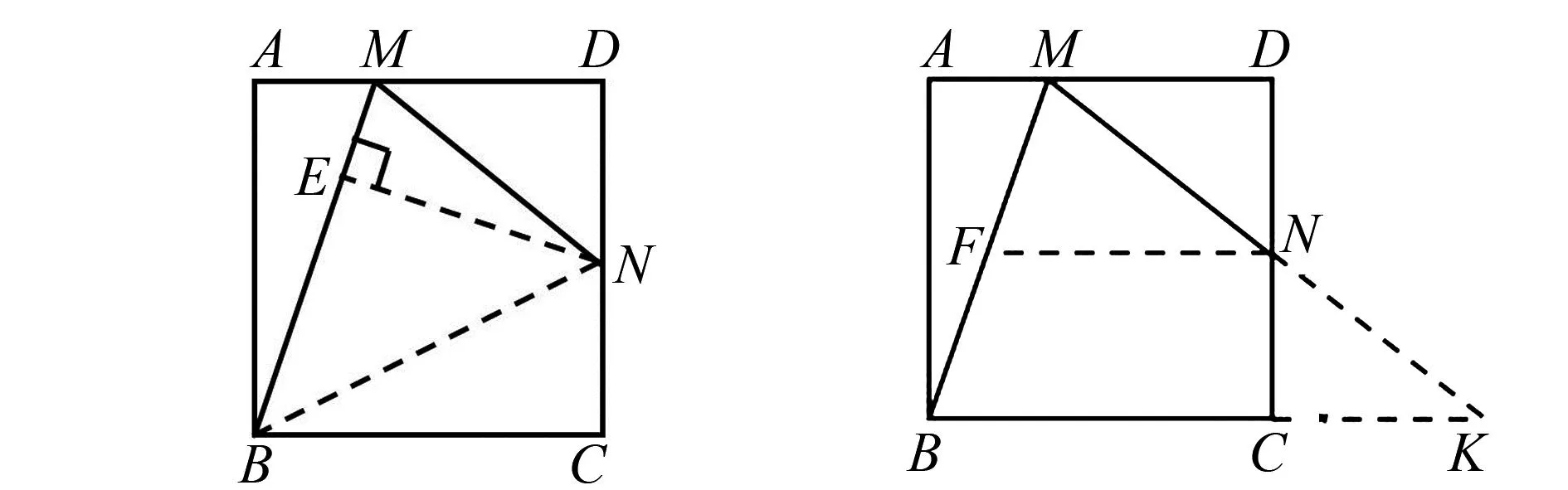
图10 证法4示意图 图11 证法5示意图

证法5 (作中位线转移角)如图11,作NF∥BC交MB于点F.证明过程从略.

在初中数学解题教学中,不要盲目追求解题数量,而应该注重解题质量.通过深入思考和精心解答一个问题,可以更好地掌握基础知识和基本技能,提高学生的解题能力和思维深度.不同的解法,涉及不同的数学知识和思想方法.通过比较不同的解法,学生可以更深入地理解数学概念和原理,培养知识系统性和关联性.这种比较和分析不同解法的过程有助于学生形成更全面的数学思维,同时提高学生的解题技巧.在深入解答一个问题的过程中,我们会发现其中的一些规律和特点,这有助于学生在解决类似问题时能够更快地找到突破口和解题思路.在“一题多解”过程中,学生会不断地重复和运用相关的数学知识,加深对知识点的记忆和理解,从而为更深层次的数学学习打下坚实的基础.

3 结束语

在初中数学解题教学中,通过解题后的“回顾与反思”,可以将问题从具体的情境中抽象出来,进一步推广引申.在推广引申过程中,还可以发现不同数学问题之间的相似关系和相联关系.通过比较不同问题的解题方法和思路,可以发现它们之间的共同之处,进而找到更一般性的解题方法或解题规律.