数形结合思想在初中数学解题中的应用

修仰尚

(福建省长汀县第三中学,福建 龙岩 366300)

数形结合是一种高效的解题方法,其侧重于利用图形的直观性来辅助数学概念的理解和问题的解决[1].文章旨在深入探讨数形结合思想在初中数学解题中的运用,揭示如何运用这一策略有效增强学生对数学概念的理解,并促进学生解题技能的提升[2].数形结合不仅仅是一种提高数学可接近性的教学工具,更是一种培养学生空间感知和逻辑推理能力的思维模式,对初中数学教学的深度和广度有着积极影响.

1 几何与图形结合的应用

例1 如图1,在Rt△ABC中,∠ACB=90°,AB=35 cm,边长12 cm的正方形CDEF内接于△ABC.求△ABC的周长.

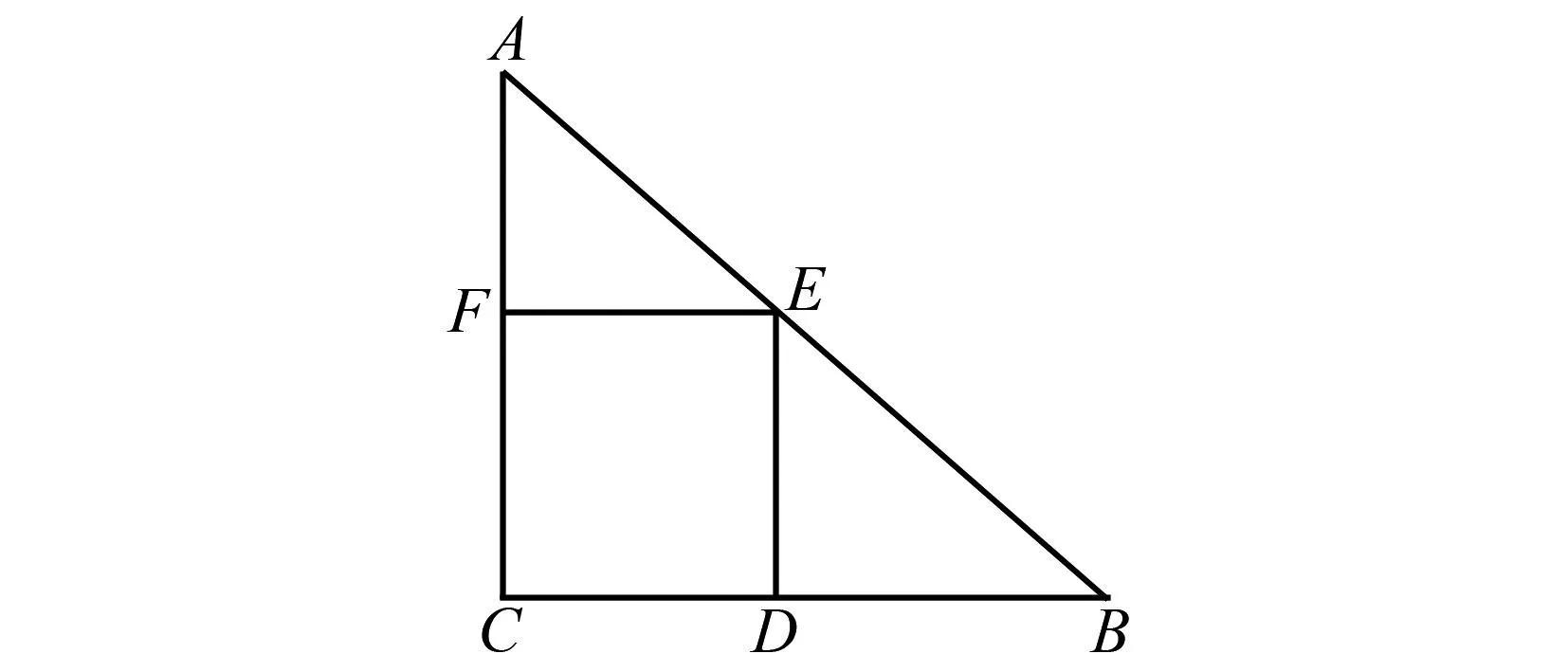
图1 例1题图

具体解题过程如下：

(1)设置变量：设BC=a,AC=b,根据勾股定理可以得到方程a2+b2=352.

(2)利用几何性质：由于正方形CDEF内接于△ABC,根据几何性质可知,Rt△AFE与Rt△ACB相似.根据相似三角形的性质,有FE：CB=AF：AC,从而可得方程12b=a(b-12).

(3)方程求解：结合这两个方程,可以得到12(a+b)=ab.通过变形可得到(a+b)2=a2+b2+2ab=1225+24(a+b).这里将a+b看作一个整体,得到一个一元二次方程.

(4)计算结果：解方程,得到a+b=49(另一解a+b=-25,不符合题意,故舍去).因此,△ABC的周长为a+b+35=49+35=84(cm).

这个例题涵盖了勾股定理、正方形的性质、相似三角形的判定与性质等知识点,其解题过程展示了数形结合思想的运用,即首先通过图形的特征建立几何关系,然后将这些关系转化为数学方程进行求解.这种方法不仅提高了解题的效率,而且增强了对几何概念和代数技能的综合理解,体现了数形结合思想在初中数学解题中的重要作用.

2 方程与不等式的图形可视化技巧

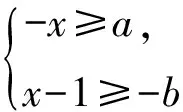
图2 例2题图

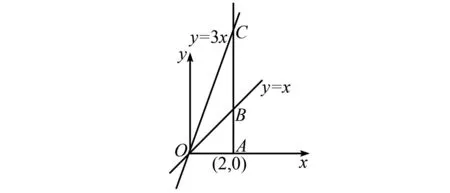
图3 例3题图

具体解题过程如下：首先确定不等式-x≥a对应数轴上的区域.这表示x的值必须小于或者等于-a.接下来,分析不等式x-1≥-b,这表明x的值可以等于b+1,但不可以大于这个值.联合这两个不等式,解集在数轴上表示为-a到b+1的闭区间.题目要求求解-x与x-1的乘积.结合两个不等式,这个乘积的最大值在x取最小值-a和x取最大值b+1时出现,即-(-a)×(b+1-1).根据题目在数轴上的标记,a和b的数值可以直接读出为a=-2和b= 4.将a和b的值代入上述代数式中,得到2×4=8.最终得出的乘积为 8,故选B.

数轴的可视化在此过程中起到了关键作用,可以直观地识别和解决问题.通过数形结合,不仅简化了问题的理解,而且提高了求解效率.

3 运用图形解析函数特性

例3 给定两个正比例函数的图象,点A(2,0)位于x轴上.过点A作x轴的垂线,与这两个函数的图象相交于点B和点C.请计算△OBC的面积.

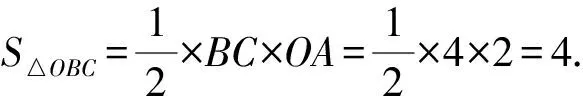
数形结合的方法加深了学生对函数概念的理解,使学生能够通过观察和分析图形来解决数学问题.这种方法不仅加深了学生对函数在坐标平面上表示方法的理解,而且为学生解决问题提供了一种强有力的视觉工具.

4 实际应用问题中的数形结合策略

例4 考虑一个反映销售数量(用x表示,单位为件)与销售费用(用y表示,单位为元)之间关系的销售情景,如图4所示,它描述了某家企业按月向其销售团队支付销售费用的两个不同计划.

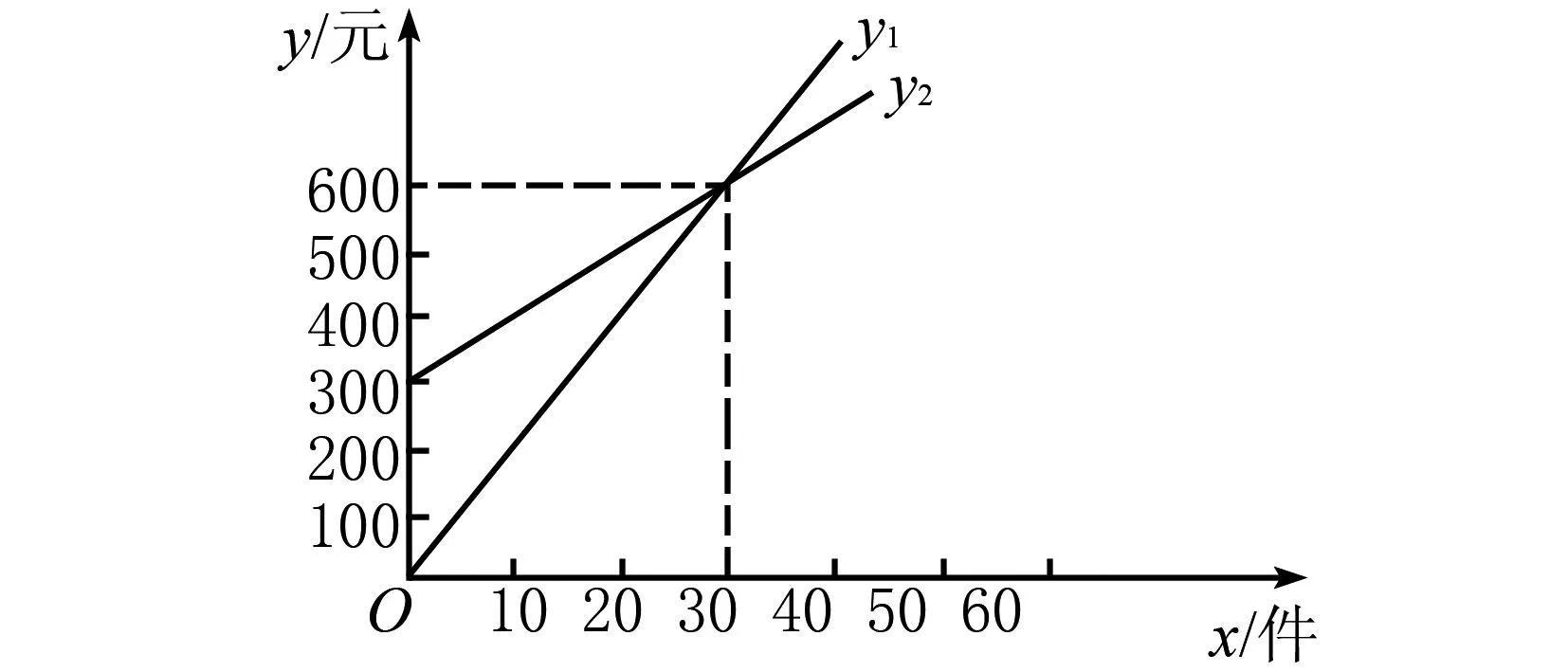
图4 例4题图

(1)根据图表数据,推导出两个支付计划下的销售费用y1和y2与销售数量x的函数关系式.

(2)从图4中解读这两个支付计划,概述每一种方案的推销费支付机制.

(3)假设你是该销售团队的一员,基于这些信息,考虑你应如何选择最适合你的薪酬计划.

具体解题过程如下：

(1)观察图表,直观看出y1与y2都随着x的增加而增加,但增长的速率和起始点不同.直线y1从原点开始,表明无基本工资,完全依赖销售量;而直线y2从y轴的300开始,表示有固定工资,再加上销量提成.

(2)分析这两条直线,可以得出它们的函数解析式y1=20x表示无底薪,是纯提成方案.y2=10x+300表示有底薪加上提成.

(3)针对不同的销售能力,推销员可以选择最优方案：销量高于30件时,选择方案y1较为有利;销量不足30件时,选择y2方案更为保险.

通过数形结合的策略,学生可以从图形中直观地理解和建立推销费与销售量之间的函数关系,进而做出基于数学分析的决策.此方法不仅使问题的解决更加直观有效,而且帮助学生认识到数学工具在现实世界经济决策中的实际应用价值.

5 数形结合解决“距离与相遇”问题

例5 一辆动车和一辆普通火车分别从西安和西宁同时出发,朝对方所在的城市前进.这里将普通火车运行的时长记为xh,两列火车之间的距离记为ykm.图5描绘了y随x变化的关系.

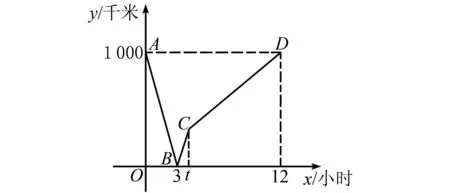
图5 例5题图

依据图5,解答下列问题：

(1)计算西安与西宁之间的实际距离及两列火车启程后多长时间相遇;确定普通火车到达目的地所需的整体时间,并推算其速度(以km/h为单位).

(2)基于图表信息,推导出动车组的平均速率.

(3)在普通火车行驶th之后,动车组正好抵达西宁.估算在这个时刻,普通火车还需行进多少千米才能抵达西安?

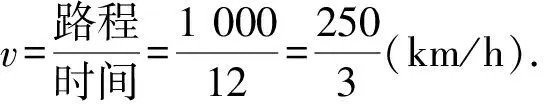
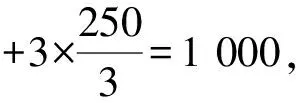
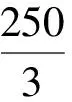
数形结合策略在解决“距离与相遇”问题中的应用,让学生通过图形化的数据理解和解决实际问题,这种方法提高了解题的准确性和效率.

6 结束语

文章探讨了数形结合思想在初中数学解题中的应用路径,从几何图形的理解到方程与不等式的图形化,再到函数特性的直观分析,最后讨论了数形结合在实际应用问题中的应用价值.这一教学方法不仅提高了学生的解题效率,而且深化了他们对数学概念的理解.展望未来,数形结合的策略应当在初中数学教学中得到更广泛的应用.