方程组AX=B与XC=D的(反)自反酉约束解
史雅萍, 刘喜富
(重庆师范大学 数学科学学院, 重庆 401331)
0 引言

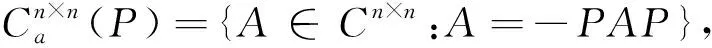

给定矩阵A,B∈Cm×n,C,D∈Cn×p,考虑如下矩阵方程组:
AX=B,XC=D.
(1)
本文主要解决如下两个问题:
问题Ⅰ:求解方程组(1)在关于广义反射矩阵P自反酉约束下的约束解;
问题Ⅱ:求解方程组(1)在关于广义反射矩阵P反自反酉约束下的约束解.
矩阵方程及其解、特殊解在物理学、计算机科学等领域有着非常广泛的应用.由于理论研究和实际应用的不同需求,对矩阵方程(组)解的性质和结构有着许多不同的约束,由此产生出不同类型的约束矩阵方程问题.对于矩阵方程AX=B的约束解也有许多研究成果,例如: (广义)自反解和(广义)反自反解[3-4],反对称正交解[5],Hermitian自反和Hermitian反自反解与非负定自反解[6].文献[1-2]分别给出矩阵方程AXB=C的自反解和矩阵方程A*XB=C的自反解与反自反解存在的充分必要条件及其解的通式.文献[7-9]给出了矩阵方程组AX=B,XC=D的Hermitian(反)自反解,广义(反)自反解,Re-nnd解与Re-pd解.文献[10]进一步给出不同矩阵方程(Ⅰ)AX=C,(Ⅱ)AX=C,XB=D,(Ⅲ)AXB=C的Hermitian解和非负定解的存在性及其解的通式.Zhang等[11]利用矩阵的奇异值分解和谱分解给出了矩阵方程组AX=B,XC=D在X*X=Ip约束下的解.另外,关于非线性矩阵方程的数值解也有许多研究成果[12-13].本文通过奇异值分解和Hermite矩阵的谱分解讨论了方程组(1)在关于广义反射矩阵P自反酉约束和关于P反自反酉约束下的解,并给出其显式表达式.这些问题尚未见相关文献报道.
在对问题Ⅰ和问题Ⅱ的求解过程中,我们将用到文献[3,11]中的以下结论.
引理1[3]给定一个广义反射矩阵P∈Cn×n,则存在酉矩阵U,使得
(2)
为简便起见,本文以下的矩阵P均为广义反射矩阵,且有分解式(2).
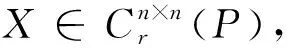
其中X1∈Cr×r,X2∈C(n-r)×(n-r),U同引理1.
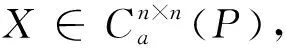
其中X1∈Cr×(n-r),X2∈C(n-r)×r,U同引理1.
引理4[11]给定矩阵A∈Cm×n,B∈Cm×p,C∈Cp×q,D∈Cn×q,n≥p.对DC*作奇异值分解如下:
其中Σ=diag(σ1,…,σr1),U1∈UCn×n,P1∈UCp×p,r1=r(DC*).对AU1,BP1作分块:
AU1=(A1,A2),BP1=(B1,B2),
其中A1∈Cm×r1,B1∈Cm×r1.对A2作奇异值分解:

其中Ω=diag(γ1,…,γr2),P2=(P21,P22)∈UCm×m,U2=(U21,U22)∈UC(n-r1)×(n-r1),P21∈Cm×r2,U21∈C(n-r1)×r2,r2=r(A2).则矩阵方程组
AX=B,XC=D
有列正交解的充要条件是:
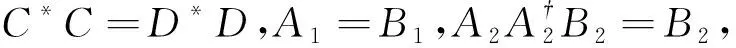
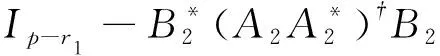

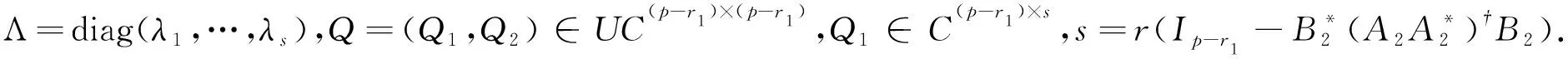
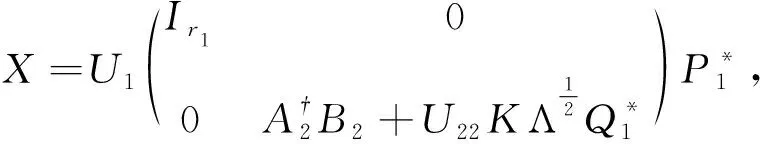
其中K∈C(n-r1-r2)×s是任意的列正交矩阵.
1 问题I的解
由引理1和引理2知,求解矩阵方程组(1)的酉自反解可等价地表示为
其中X1∈UCr×r,X2∈UC(n-r)×(n-r).
记
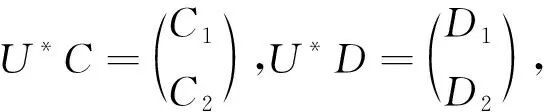
(3)
这里:A1,B1∈Cm×r,A2,B2∈Cm×(n-r),C1,D1∈Cr×p,C2,D2∈C(n-r)×p. 可得
(4)
求解式(4)的酉矩阵解等价于求解矩阵方程组(1)的酉自反解.
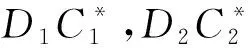
(5)

A1U1=(A11,A12),A2U2=(A21,A22),
B1P1=(B11,B12),B2P2=(B21,B22),
(6)
其中A11∈Cm×r1,B11∈Cm×r1,A21∈Cm×r2,B21∈Cm×r2.对A12,A22作奇异值分解:
(7)
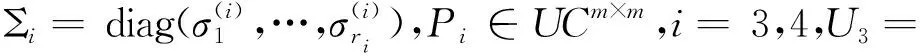
(8)

(9)
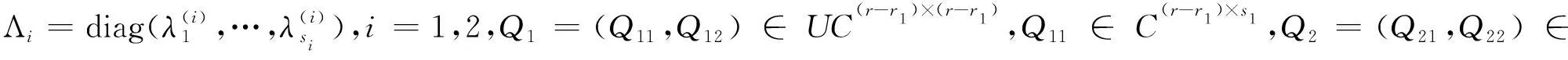
(10)
其中
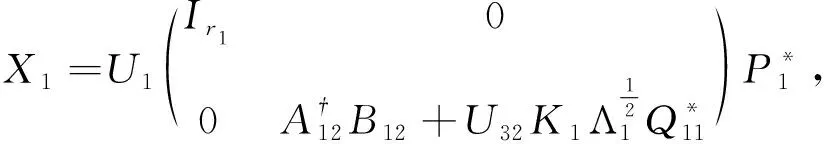
K1∈C(r-r1-r3)×s1,K2∈C(n-r-r2-r4)×s2是任意的列正交矩阵.
于是得到以下定理.
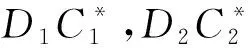
2 问题II的解
同理,由引理1和引理3知求解矩阵方程组(1)的酉反自反解等价于求解
其中X1∈Cr×(n-r),X2∈C(n-r)×r.
对AU,BU,U*C,U*D作分块同式(3),可得
(11)
求解式(11)的列正交解等价于求解矩阵方程组(1)的酉反自反解.
由于求解(11)的列正交解需满足r≥n-r,n-r≥r,于是r=n-r.即广义反射矩阵P有如下分解式:
(12)
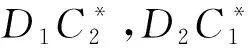
(13)

A1U1=(A11,A12),A2U2=(A21,A22),
B2P1=(B11,B12),B1P2=(B21,B22),
(14)
其中A11,B11∈Cm×r1,A21,B21∈Cm×r2.对A12,A22作奇异值分解:
(15)
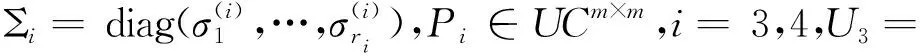
(16)
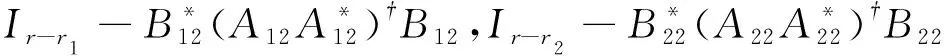
(17)
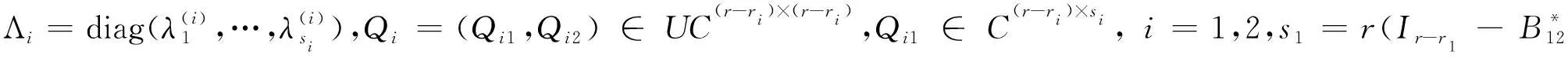
(18)
其中
其中K1∈C(r-r1-r3)×s1,K2∈C(r-r2-r4)×s2是任意的列正交矩阵.
于是得到以下定理.
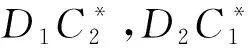
3 数值算例
本节所有数值计算都是在windows 10系统21H2版本中用Matlab 2020b编程计算.
例1令m=5,n=9,p=6,给定矩阵A,B,C,D如下:

可以得到问题I的解X如下:
例2令m=5,n=8,p=6,给定矩阵A,B,C,D如下:

可以得到问题II的解X如下:
4 总结
本文利用奇异值分解、谱分解、(反)自反矩阵的分解表达式和矩阵分块给出了方程组(1)在关于给定广义反射矩阵P自反酉约束和反自反酉约束下的解的显式表达式,并利用数值算例证明其有效性.

