地铁盾构双线隧道地表横向变形特性与预测*
吴锋波,郑卫强,窄佐磊
(1.河北地质大学城市地质与工程学院,河北 石家庄 050031; 2.河北省地下人工环境智慧开发与管控技术创新中心,河北 石家庄 050031; 3.自然资源部京津冀城市群地下空间智能探测与装备重点实验室,河北 石家庄 050031;4.东华理工大学土木与建筑工程学院,江西 南昌 330013)
0 引言
北京地铁双线区间隧道施工方法多为盾构法,其设备较先进,机械化程度较高。双线隧道周围土层因盾构施工造成土体沉降固结,地表产生变形[1]。当地表变形值过大时,可能引起周边建筑、地下管线等的过量变形,进一步影响工程环境对象的安全,需深入开展盾构双线隧道的地表变形研究。
众多因素影响地铁盾构双线隧道地表横向变形,当前主要研究方法有解析计算法、经验公式法、模型试验法与数值模拟法等。Peck[2]基于芝加哥地铁双线隧道研究认为其沉降槽对称分布,计算时可采用大圆半径替代。New等[3]认为最大位移会偏离中心轴线,故需对Peck公式进行修正,预测不对称的沉降槽时采用高斯曲线补偿。Attewell[4]发现沉降槽形态受盾构隧道直径、埋深、地表附近地层性质影响较大。Cording等[5]通过实测数据发现双线盾构横向地表变形沉降槽非对称。Suwansawat等[6]采用超几何方法计算盾构隧道变形。在国内,刘波等[7]提出双线盾构隧道平行开挖修正Peck公式。魏纲[8]对双线盾构隧道施工引起的土体变形、环境对象影响及控制开展了相关研究。邱明明等[9-10]、芮瑞等[11]研究表明,双线隧道沉降槽曲线随双隧中心间距L的增大逐渐由V形转变为W形,并提出了地层预测模型。卢健等[12]研究得出,双线隧道施工先行隧道对土层扰动大于后行隧道。赵乙丁等[13]认为,双隧净距大小与沉降槽宽度呈正相关。牟天光等[14]认为,影响地表变形的最主要因素为盾构隧道埋深。宋方方[15]分析了盾构双线隧道地表沉降曲线的相关影响因素。
现有研究一般基于一定数量的工程案例,采用经验公式与数值模拟相结合的方法对地铁盾构双线隧道的地表横向变形进行预测,工程适用性难免受到限制。北京地铁建设积累了丰富的盾构双线隧道地表变形实测资料,为该项研究的深入开展提供了可靠的数据支撑。基于丰富实测数据的北京地铁盾构双线隧道地表横向变形研究十分必要,具有重要的理论和实践指导意义。
1 地铁盾构双线隧道地表变形分析
1.1 数值模拟计算方案
地表变形影响因素可分为主观因素和客观因素。主观因素包括人员的工作状态、技术水平、施工管理水平等,一般难以量化考虑;客观因素主要包括盾构机类型、地质条件、隧道覆土厚度(或中心埋深)、结构断面形式与大小、双隧水平净间距(或中心水平间距)、盾构管片类型、隧道上部荷载等。各因素影响相互作用、交织,有明显的耦合效应。
本文根据文献[16]的分类结果,分别对北京地区黏性土地层和砂卵石地层地铁双线盾构隧道开挖引起的地表变形进行研究。地下水位一般较深,暂未考虑其影响。隧道横断面一般为标准断面,综合考虑选取隧道覆土厚度(或中心埋深)、双隧水平净间距(或中心水平间距)等可量化因素,结合其常规地表变形情况开展数值模拟研究,以量化确定盾构双线隧道不同空间位置关系之下地表变形特性。数值模拟计算软件为FLAC3D,具体计算方案如下。
1)盾构双线隧道左、右线均为标准断面,隧道直径D为6.0m,隧道上方最大覆土厚度为19.0m,计算模型大小为90.0m(x方向)×36.0m(y方向)×55.0m(z方向)。计算数值模型中,均采用实体单元,其中土体使用莫尔-库仑本构模型,盾构衬砌使用线弹性模型。顶面设置为自由边界,其余5面设置法向约束。
2)隧道管片衬砌厚0.3m,隧道内径5.4m,管片混凝土为C50,考虑管片连接和拼装方法影响,需对管片刚度进行修正,修正系数为0.87,弹性模量为30GPa,密度为2 500kg/m3,体积模量为16.67GPa,剪切模量为15.22GPa。
3)黏性土地层概化为杂填土、粉土和粉质黏土,砂卵石地层概化为杂填土、粉质黏土、粉细砂、卵石,地层厚度和主要物理力学参数如表1所示。
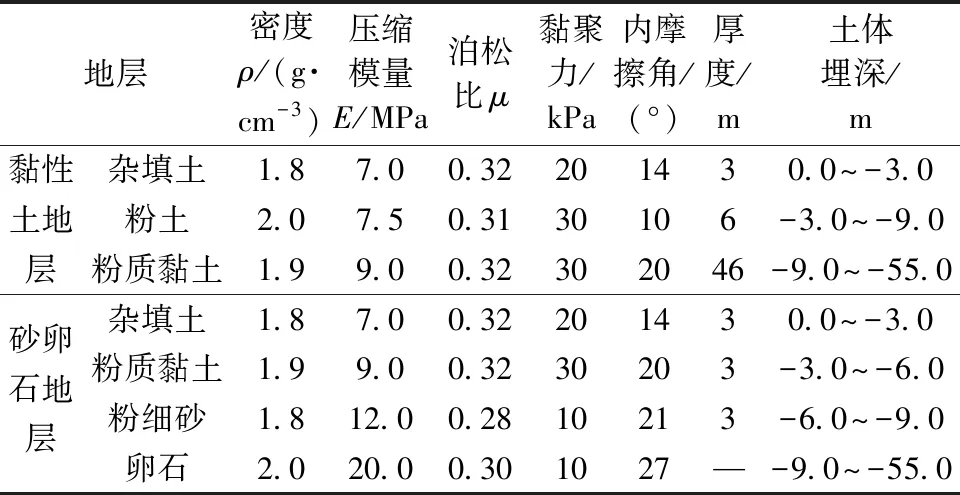
表1 不同地层物理力学参数
4)隧道长度均为36.0m,每次开挖进尺为1.5m。左侧隧道先行开挖,贯通后开始右侧隧道开挖,两隧道开挖方向相同。模型分为5种开挖方案:①方案1 双隧左右水平,隧道中心埋深Z0=13m,1号隧道为左侧隧道,双隧水平净间距依次取值为3,6,9,12,15,18,21,24,30m,共计9种工况。②方案2 双隧左右水平,Z0=17m,2号隧道为左侧隧道,双隧水平净间距取值与方案一相同,共计9种工况。③方案3 双隧左右水平,Z0=22m,3号隧道为左侧隧道,双隧水平净间距取值与方案1相同,共计9种工况。④方案4 双隧上下交错,左侧隧道为中心埋深13m的1号隧道,右侧隧道为中心埋深22m的3号隧道及其右侧9座隧道,共计10种工况。⑤方案5 双隧上下交错,左侧隧道为中心埋深22m的3号隧道,右侧隧道为中心埋深13m的1号隧道及其右侧9座隧道,共计10种工况。盾构隧道开挖方案如图1所示。
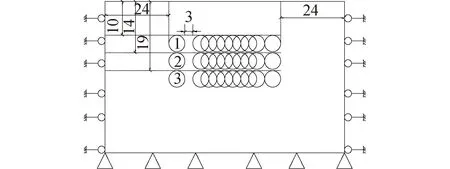
图1 模拟开挖方案示意(单位:m)
5)模型监测点布置:因数值模拟计算结果需具有典型性与可对比性,模型监测点均设置在Y=18.0m处地表,以左侧隧道中线上方地表为水平坐标原点,左、右按间距0.5D设置监测点,具体位置如图2所示。

图2 模型监测点布置示意
1.2 计算结果分析
根据模型开挖方案,反映左、右2座隧道空间位置关系变化的计算工况共计47种,取监测点处的结果研究分析。
1.2.1双隧左右水平(方案1~3)
定义盾构双线平行隧道的相对间距系数R1=L/Z0,其中L为双隧中心水平间距,Z0为隧道中心埋深。盾构双线隧道左右平行、中心水平间距L不同时,数值模拟计算结果如表2、图3所示。
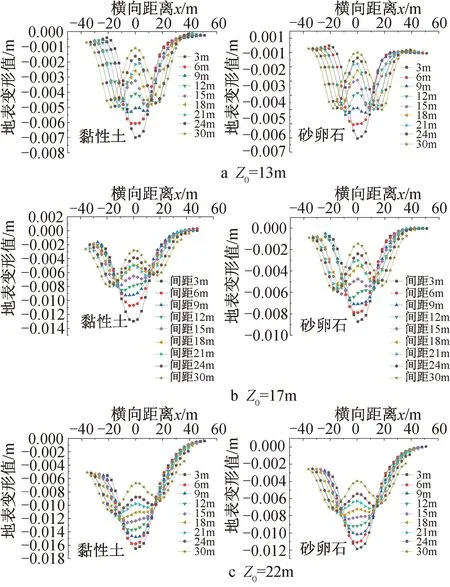
图3 双隧左右平行时地表沉降槽曲线
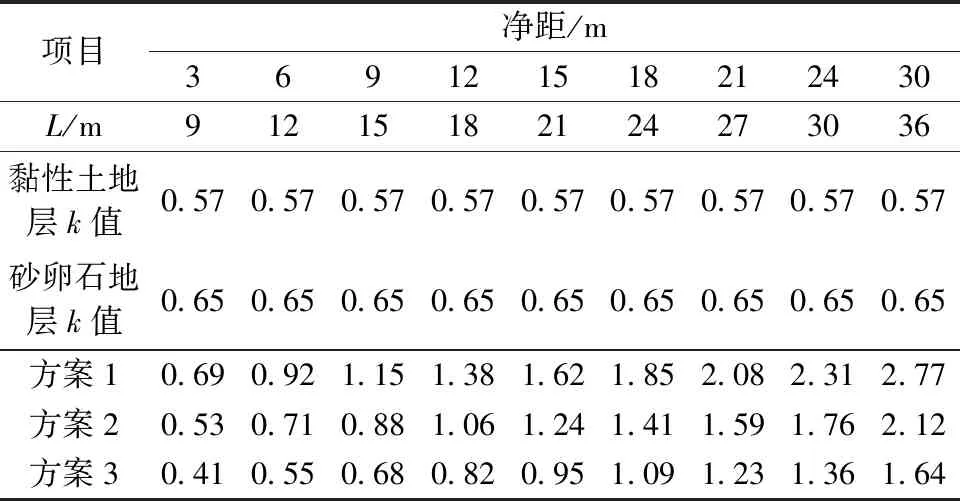
表2 双隧左右水平时相对间距系数R1值
由表2和图3a可知,隧道中心埋深Z0=13m且R1≤0.92时,双线隧道最终地表沉降曲线形态近似为V形或U形,底部窄而尖,R1值越小特征越明显,最大沉降值近似位于两隧道中部;0.92 由表2和图3b可知,隧道中心埋深Z0=17m且R1≤0.88时,双线隧道最终地表沉降曲线形态近似为V形或U形,底部窄而尖,R1值越小特征越明显,最大沉降值近似位于两隧道中部;0.88 由表2和图3c可知,隧道中心埋深Z0=22m且R1≤0.82时,最终地表沉降曲线形态近似为V形或U形,R1值越小特征越明显,随着R1值的增加,沉降槽底部跨度增大,最大沉降值近似位于两隧道中部;R1>0.82时,最终地表沉降曲线底部出现双峰值,形态近似为W形,R1值越大双峰值特征越明显,最大沉降值约位于左侧隧道(先行隧道)中心轴线上方。 1.2.2双隧上下交错(方案4,5) 定义盾构双线隧道上下交错时的相对间距系数R2=L/|Z0左-Z0右|,其中Z0左,Z0右分别为左、右隧道中心埋深。盾构双线隧道上下交错、中心水平间距L不同时,数值模拟计算结果如表3、图4所示。 图4 双隧上下交错时地表沉降槽曲线 表3 双隧上下交错时相对间距系数R2值 由表3和图4a可知,左侧隧道中心埋深13m、右侧隧道22m且R2≤1.25时,最终地表沉降曲线形态近似为V形或U形,R2值越小特征越明显,最大沉降值近似位于两隧道中部;1.25 由表3和图4b可知,左侧隧道中心埋深22m、右侧隧道13m且R2≤1.25时,最终地表沉降曲线形态近似为V形或U形,R2值越小特征越明显,最大沉降值近似位于两隧道中部;1.25 Peck公式具有模型简单、实用有效的特点,在城市地铁隧道地表变形预测方面有较好应用。根据文献[17-18],地铁隧道工程地表横向变形预测Peck公式可写为: (1) 式中:S(x)为隧道两侧横向上距隧道中心x处的地面沉降量(m);x为隧道两侧横向上距隧道中心距离(m);D为隧道直径(m);Vl为地层损失率(%);k为地表沉降槽宽度参数;Z0为隧道中心埋深(m)。 根据盾构双线隧道最终地表变形形态理论分析结果及与相对间距系数R1,R2值的对应关系,建立北京地区黏性土地层和砂卵石地层的地铁盾构双线隧道地表变形预测公式如下。 双线平行隧道相对间距系数R1≤0.82~0.92(建议取值0.87),或双线交错隧道相对间距系数R2≤1.25时,最终地表变形形态为单沉降槽,可根据式(1)建立地表变形预测公式: (2) 式中:D总为隧道等效直径,按等面积替代法确定,可取值为(L+D)(m);Vl总为最终单沉降槽的地层损失率(%);k总为最终单沉降槽的宽度参数;Z0总为等效隧道中心埋深(m),双线交错隧道可取左、右隧道中心埋深的平均值。 双线平行隧道相对间距系数0.82~0.92 将式(1)代入文献[7]所提出的双线隧道地表变形公式,可得出变形预测Peck公式为: (3) 式中:Vl左,Vl右分别为左、右隧道的地层损失率(%);k左,k右分别为左、右隧道的沉降槽宽度参数;Z0左,Z0右分别为左、右隧道的中心埋深(m);L为双隧中心间距(m)。 双线平行隧道Z0左=Z0右时,可近似按Vl左=Vl右,k左=k右取值进行地表变形预测。双线交错隧道可近似按沉降值较大的沉降槽变形情况选取参数进行地表变形预测。 双线平行隧道相对间距系数R1≥2.08~2.12(建议取值R1≥2.10),或双线交错隧道相对间距系数R2≥3.00时,最终地表变形形态为近似独立的双沉降槽,可根据式(1)分别预测左、右隧道各自的地表变形情况。 两沉降槽在双线中部有一定重合时,可综合叠加获得最终沉降槽,进而确定双线隧道的地表变形影响区域;两隧道间距较大、各自地表沉降槽近似完全独立时,可分别按两沉降槽分布情况确定地表变形区域。 基于文献[16]的研究方法,补充收集北京地区黏性土地层和砂卵石地层的地铁盾构双线地表变形资料,对沉降槽最大沉降值、地层损失率Vl和沉降槽宽度参数k进行统计分析,结果可作为双线平行隧道、最终沉降槽形态为W形时地表变形的预测参数。双线交错隧道、最终沉降槽形态为W形时可做一定参考。双隧距离较近,最终沉降槽形态为V形或U形的情况,需进一步收集相关实测资料,开展预测参数的拟合和统计分析工作。 地表沉降槽的最大沉降值统计结果如图5所示。 图5 最大沉降值分布频率直方图 基于统计结果,在北京黏性土地层中采用盾构施工的61个地表沉降槽中沉降最大值分布范围为 2.61~ 32.73mm, 均值为12.18mm,标准差为7.02mm,中位数为10.40mm;形态近似为正态分布(图5中拟合曲线为正态分布曲线,下同),主要分布区间为8~10mm;偏态系数SK=1.149,为高度右偏分布;峰态系数K=1.171,为尖峰分布。 砂卵石地层盾构开挖的38个地表沉降槽中沉降最大值为20.81mm,最小值为2.99mm,平均值为10.00mm,标准差为4.12mm,中位数为10.09mm;近似为正态分布,数值主要分布在8~12mm;偏态系数SK=0.455,为中等右偏分布;峰态系数K=0.357,为尖峰分布。 地表沉降槽的地层损失率Vl的统计结果如图6所示。 黏性土地层中53个地表沉降槽拟合获得有效的地层损失率Vl值,其分布范围为0.24%~8.40%,平均值为3.51%,标准差为2.48%,中位数为3.31%,近似为多峰值分布,主要分布区段为0~1.0%和3.0%~4.0%。 砂卵石地层中剔除地铁试验段的异常值后,37个地表沉降槽地层损失率最大值为8.86%,最小值为0.51%,平均值为2.33%,标准差为2.13%,中位数为1.22%;近似为半正态分布,主要分布在0~1.0%。 地表沉降槽宽度参数k的统计结果如图7所示。 图7 宽度参数分布频率直方图 黏性土地层中64个地表沉降槽宽度参数分布范围为0.26~0.98,平均值为0.54,标准差为0.20,中位数为0.49;近似为正态分布,主要分布区段为0.3 ~ 0.4;偏态系数SK= 0.736,为中等右偏分布;峰态系数K=-0.443,为扁平分布。 砂卵石地层中37个地表沉降槽宽度参数最大值为1.14,最小值为0.22,平均值为0.53,标准差为0.24,中位数为0.44;近似为正态分布,数值主要分布在0.4~0.5;偏态系数SK=1.439,为高度右偏分布;峰态系数K=1.176,为尖峰分布。 北京地铁16号线二期工程温阳路站—稻香湖路站区间起于温阳路与北清路十字路口、北清路北侧的温阳路站,到达稻香湖路与北清路十字路口的稻香湖路站。区间起止里程为BK3+ 321.920—BK5+333.600,长约2 011.68m。区间隧道施工使用盾构机进行开挖,始发站为温阳路站,接收站为稻香湖站。盾构隧道管片内径为5.4m、外径为6.0m,厚度为0.3m,每片管片长1.2m,分为6块,管片为错缝拼装方式[19]。 工程勘察显示,地表以下55m深度范围内地层从上往下主要为粉土填土、杂填土、粉土、粉质黏土、中粗砂、卵石层。区间隧道结构主要在粉土、粉质黏土层中,上覆地层为粉土填土、杂填土、粉土和粉质黏土。 选取该工程的典型工程断面开展地表变形预测,该断面隧道中心埋深14.3m,双线隧道净间距9m,盾构开挖主要位于粉土与粉质黏土层,断面无上层滞水层。 该断面与数值模拟计算中方案1中第3个工况(Z0=13m,净距9m,R1=1.15)接近,初步判断地表最终变形为相互影响较大的双沉降槽。根据附近已有盾构隧道施工地表变形数据的经验对比,选取地层损失率Vl左=Vl右=0.95%,沉降槽宽度参数k=0.66,代入式(2)进行地表变形计算。 对地表变形预测公式计算结果、数值模拟计算结果与变形实测数据进行对比分析,得到盾构双线隧道地表横向沉降槽对比曲线,如图8所示。 图8 典型监测断面地表沉降槽对比曲线 结果表明,地表变形预测公式计算结果与实际监测结果较一致,其最终沉降槽曲线形态均为相互影响较大的W形曲线,该预测公式具有较好适用性。 此外,地表变形预测公式的参数取值对预测结果影响较大,工程实际应尽量选取邻近典型工程的沉降槽拟合参数开展预测计算。如果缺少相关资料,可根据本文的沉降槽预测参数统计分析结果选择适宜的参数数值。 1)地铁盾构双线隧道的地表变形与左、右隧道的空间位置关系密切相关,理论计算结果表明一定地层条件之下随着隧道中心间距的增加,双线隧道地表沉降槽逐渐由V形(或U形)转变为W形。双隧左右水平时,2个沉降槽的形态近似相同;双隧上下交错时,2个沉降槽为一大一小2种形态。 2)首次定义地铁盾构双线隧道的相对间距系数R1和R2,理论计算结果表明,R1≤0.87或R2≤1.25时,最终地表变形为单沉降槽;0.87 3)建立了地铁盾构双线隧道地表变形预测公式,对北京地铁盾构双线地表变形资料进行拟合分析,分别获得了黏性土地层、砂卵石地层的地层损失率Vl和沉降槽宽度参数k的统计结果,为变形预测参数取值提供了参考。典型工程案例验证结果表明,该预测公式具有很好适用性。 4)建议进一步开展双隧距离较近、最终变形为单沉降槽等情况之下的工程变形实测资料拟合和参数统计分析研究,为类似工程的变形预测提供基础性参数值。
2 地铁盾构双线隧道地表变形预测
2.1 双隧距离较近,单沉降槽
2.2 双隧距离适中,相互影响的双沉降槽
2.3 双隧距离较远,近似独立的双沉降槽
3 地表变形预测参数取值
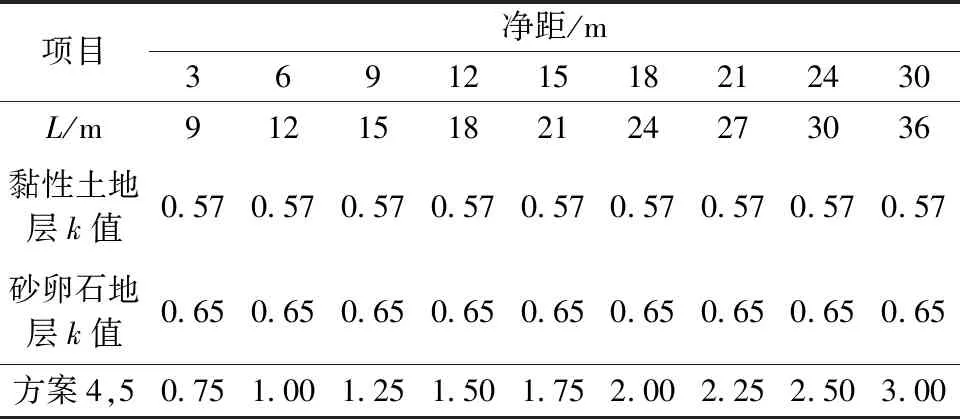
3.1 最大沉降值
3.2 地层损失率Vl
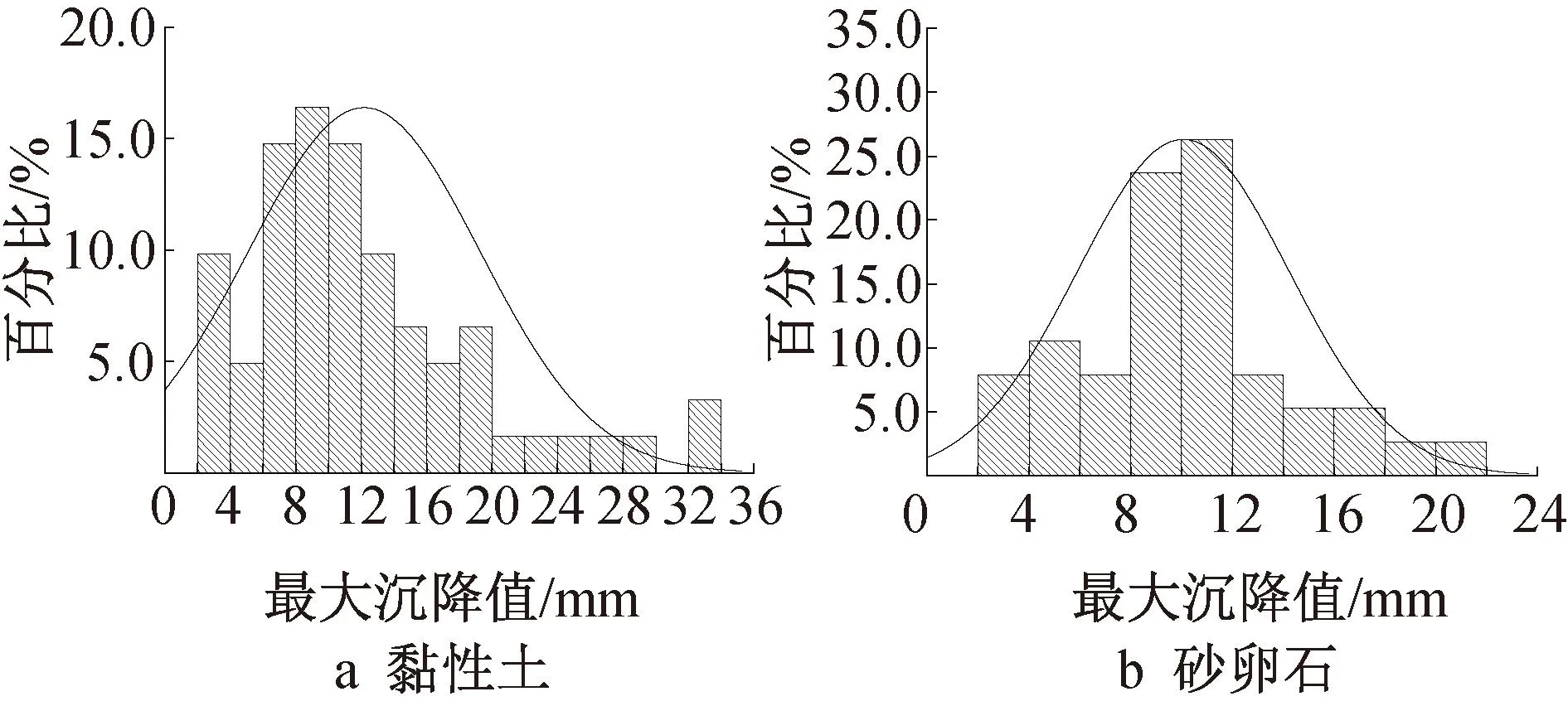
3.3 地表沉降槽宽度参数k
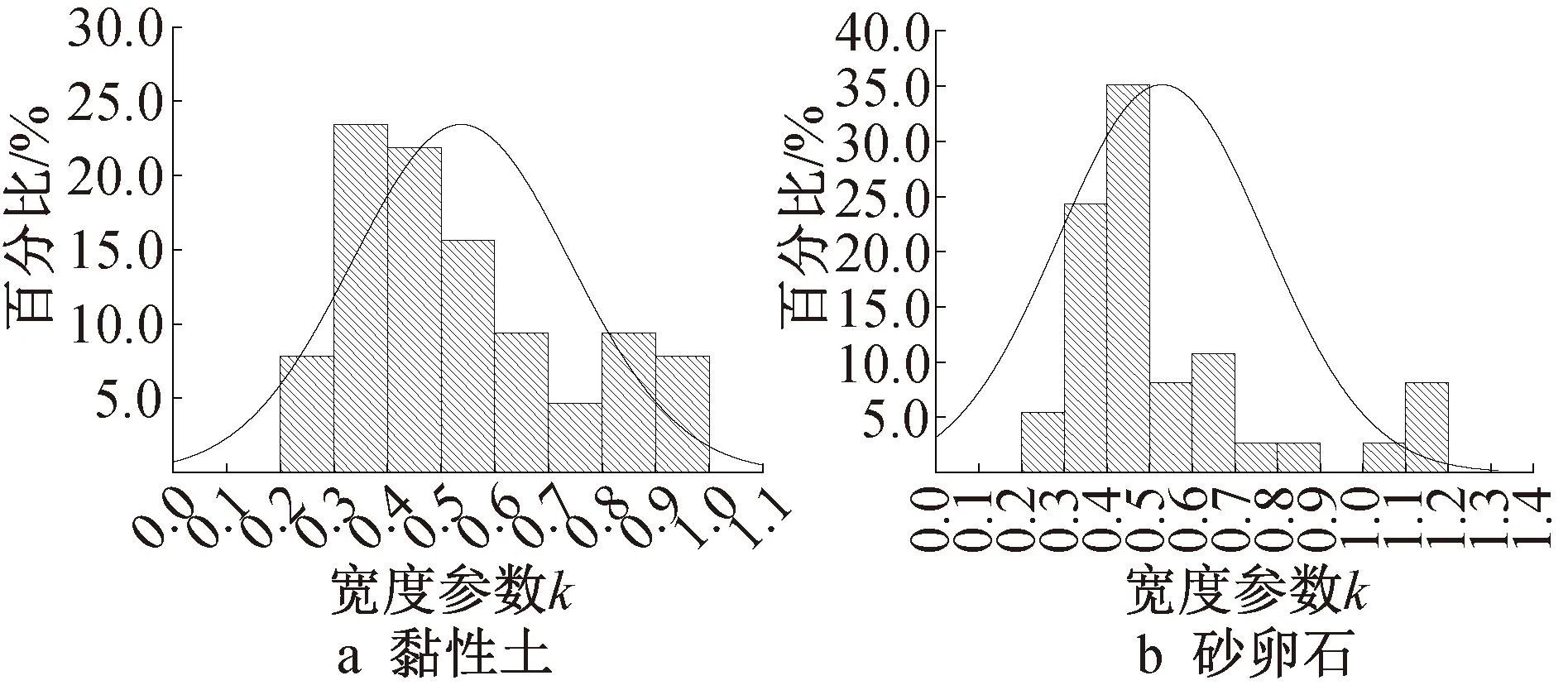
4 典型工程案例验证
4.1 工程概况
4.2 地质条件
4.3 监测断面变形预测
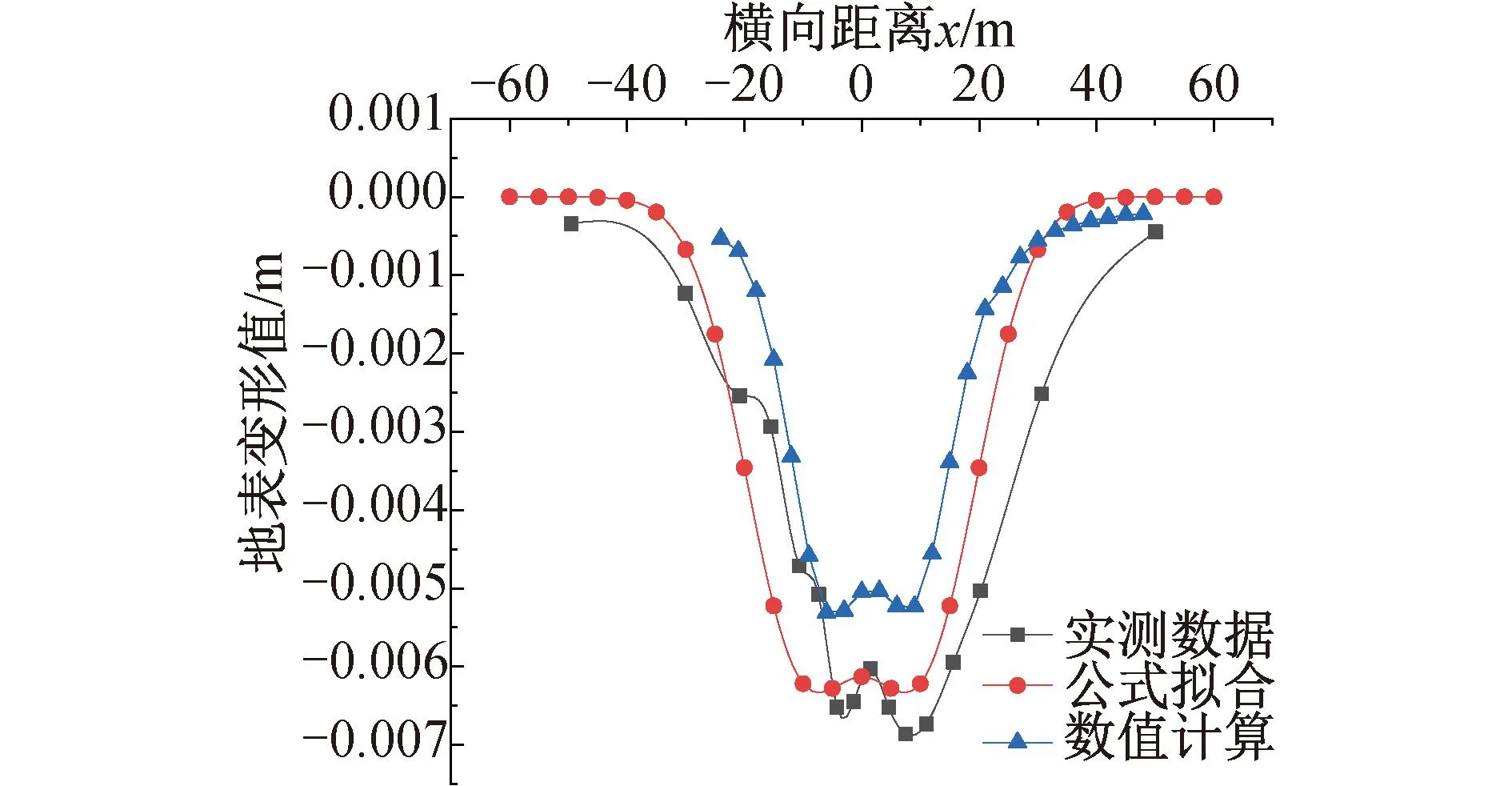
5 结语

