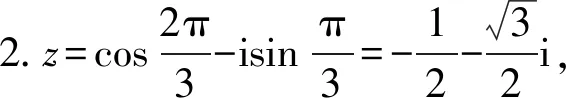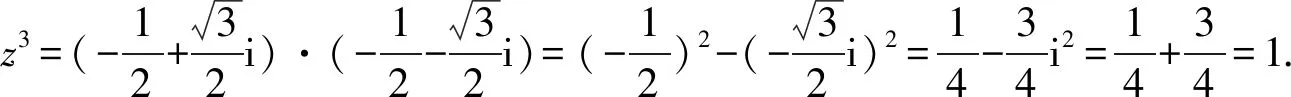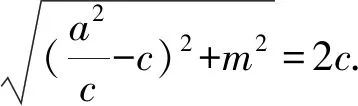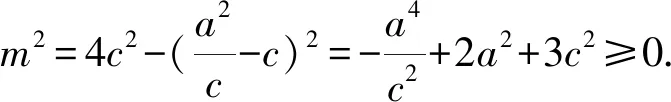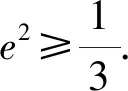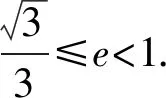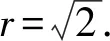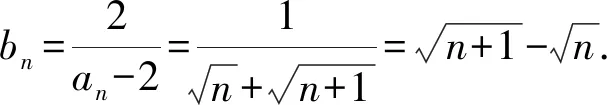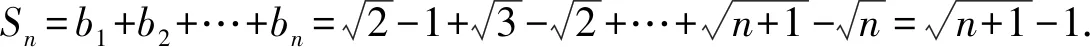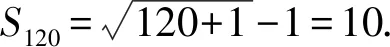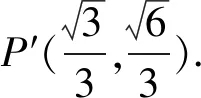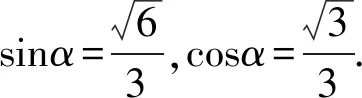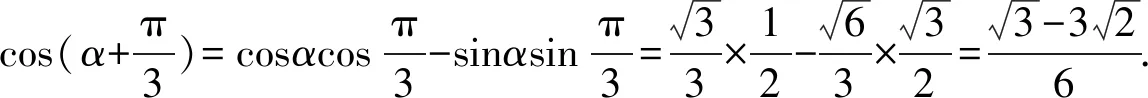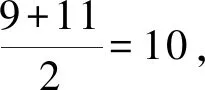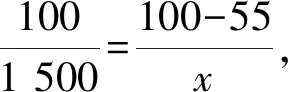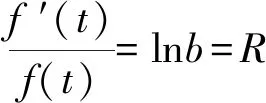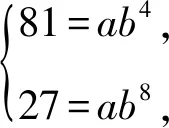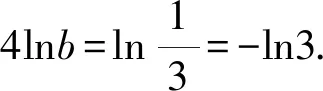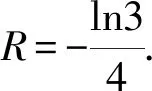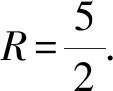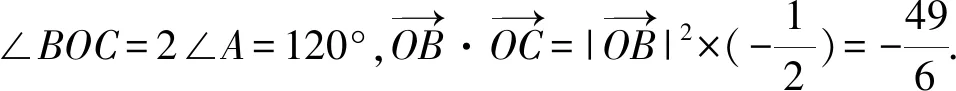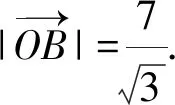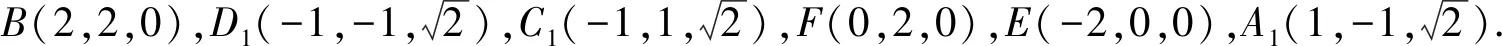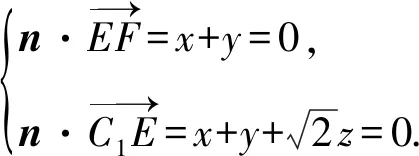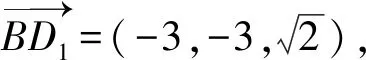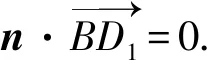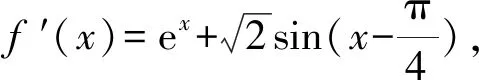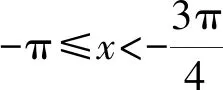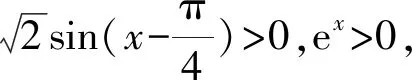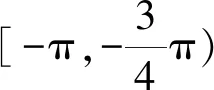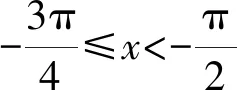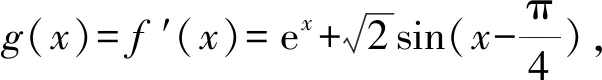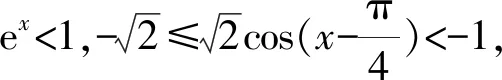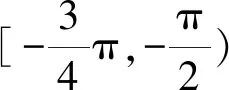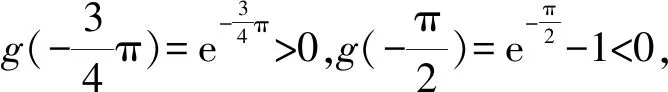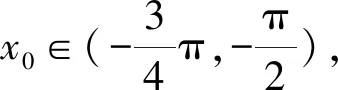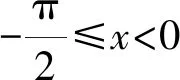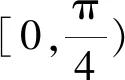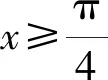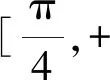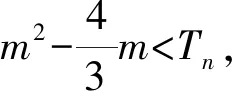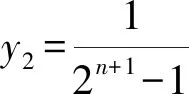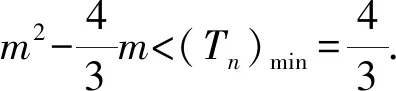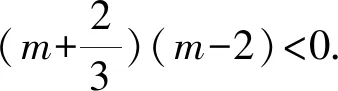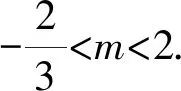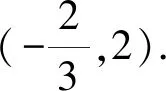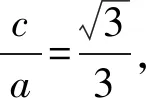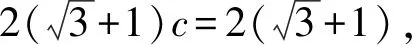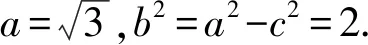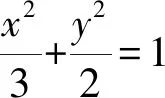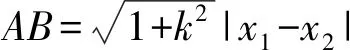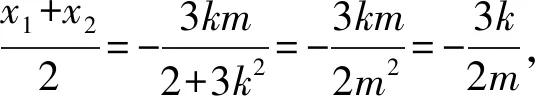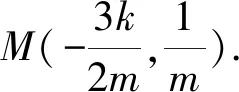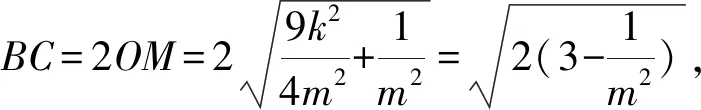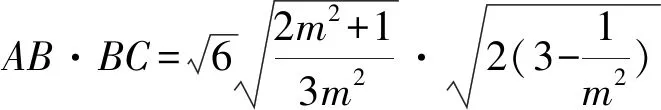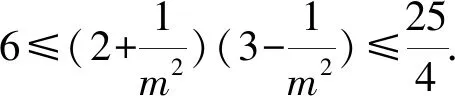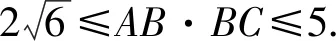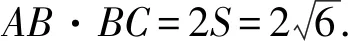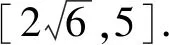2024年新高考数学模拟卷(四)

李春林

(天水市第九中学,甘肃 天水 741020)

(河南、山西、江西、安徽、甘肃、青海、内蒙古、黑龙江、吉林、宁夏、新疆、陕西)

第Ⅰ卷(选择题)

一、选择题：本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1.已知集合A={x|x2<4},B={x|y=lg(1-x)},则A∩B=( ).

A.(-2,1] B.(1,2] C.(-2,1) D.(0,2)

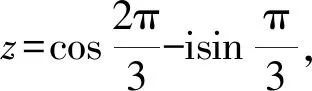
A.1 B.-1 C.i D.-i

3.已知平面向量a,b和实数λ,则“a=λb”是“a与b共线”的( ).

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

4.已知函数f(x)=(x+a-2)(x2+a-1)为奇函数,则f(a)的值是( ).

A.0 B.-12 C.12 D.10

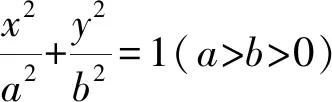
6.已知圆C:x2+y2+2x-2y=0,直线l的横纵截距相等且与圆C相切﹐则满足条件的直线l有( )条.

A.1 B.2 C.3 D.4

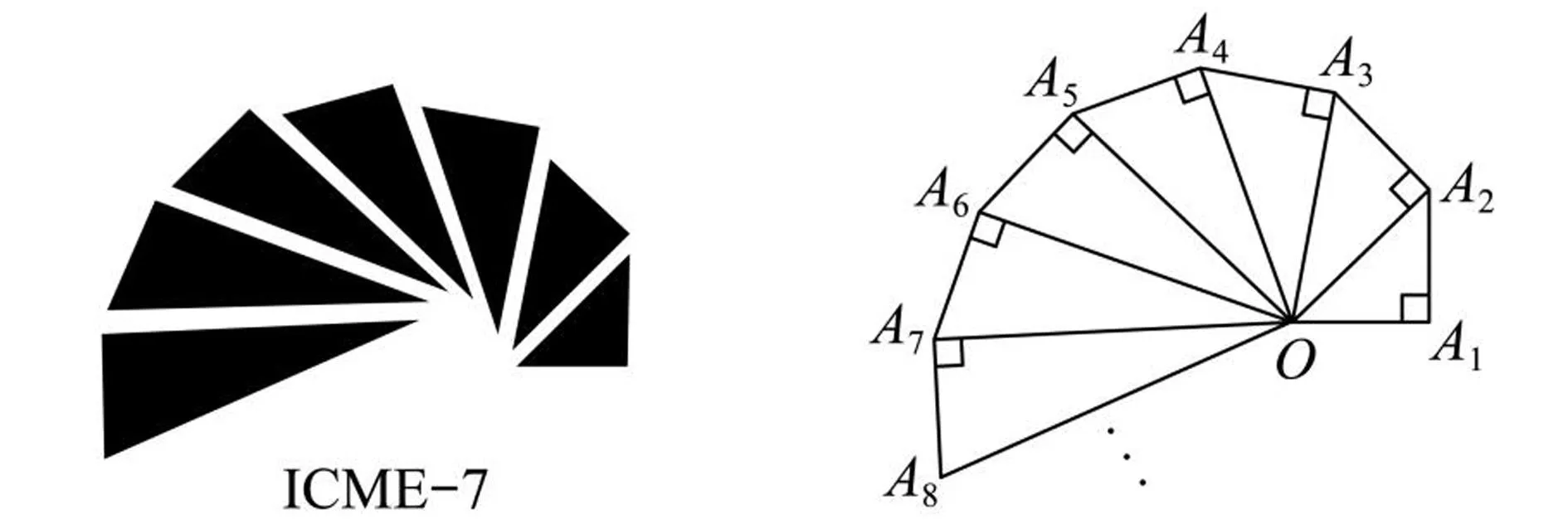
图1 ICME-7会徽图案 图2 第7题示意图

A.8 B.9 C.10 D.11

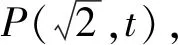
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.

9.下列说法正确的是( ).

A.线性回归方程中,若线性相关系数r越大,则两个变量的线性相关性越强

B.数据1,3,4,5,7,9,11,16的第75百分位数为10

C.根据分类变量X与Y的成对样本数据,计算得到χ2=3.937,根据小概率值α=0.05的独立性检验(x0.05=3.841),可判断X与Y有关联,此推断犯错误的概率不大于0.05

D.某校共有男女学生1 500人,现按性别采用分层抽样的方法抽取容量为100人的样本,若样本中男生有55人,则该校女生人数是675

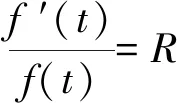
C.排气20分钟后,人可以安全进入车库

D.排气24分钟后,人可以安全进入车库

11.已知函数f(x)=(x2-x+1)ex,则( ).

A.f(x)有两个极值点

B.f(x)在x=1处的切线方程为y=2ex-e

C.f(x)在[-1,1]上的值域为[3e-1,e]

D.当a<1时,方程f(x)=a有且仅有一解

第Ⅱ卷(非选择题)

三、填空题:本题共3小题,每小题5分,共15分.

12.从一颗骰子的六个面中任意选取三个面,其中恰有两个面平行的不同选法共有____种(用数字作答).

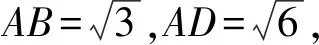
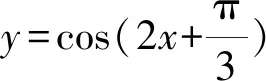
四、解答题：本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.

(1)求∠A;

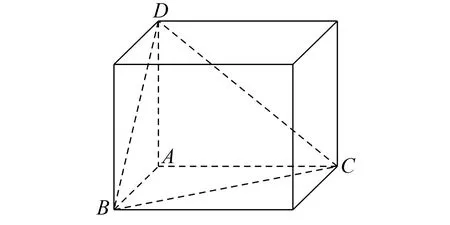
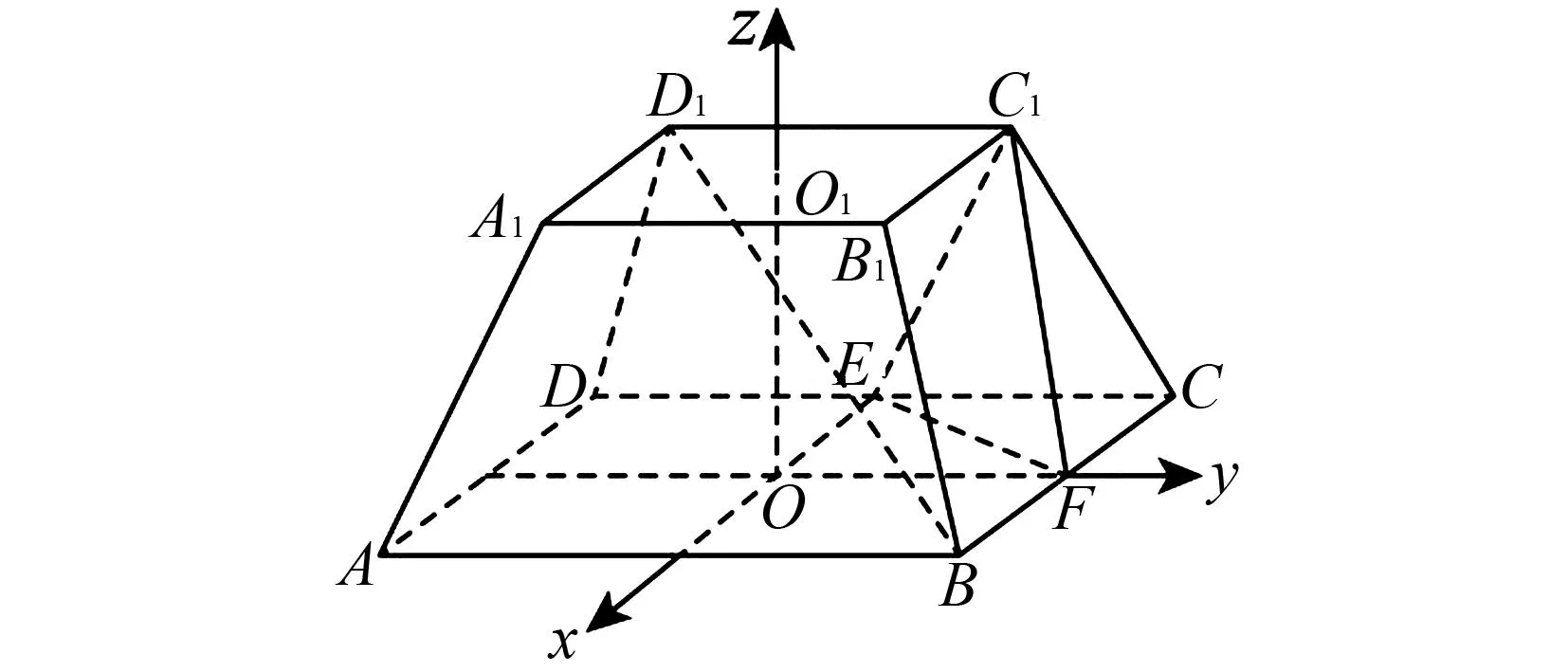
16.如图3,四棱台ABCD-A1B1C1D1中,上、下底面均是正方形,且侧面是全等的等腰梯形,AB=2A1B1=4,E,F分别为DC,BC的中点,上下底面中心的连线O1O垂直于上下底面,且O1O与侧棱所在直线所成的角为45°.

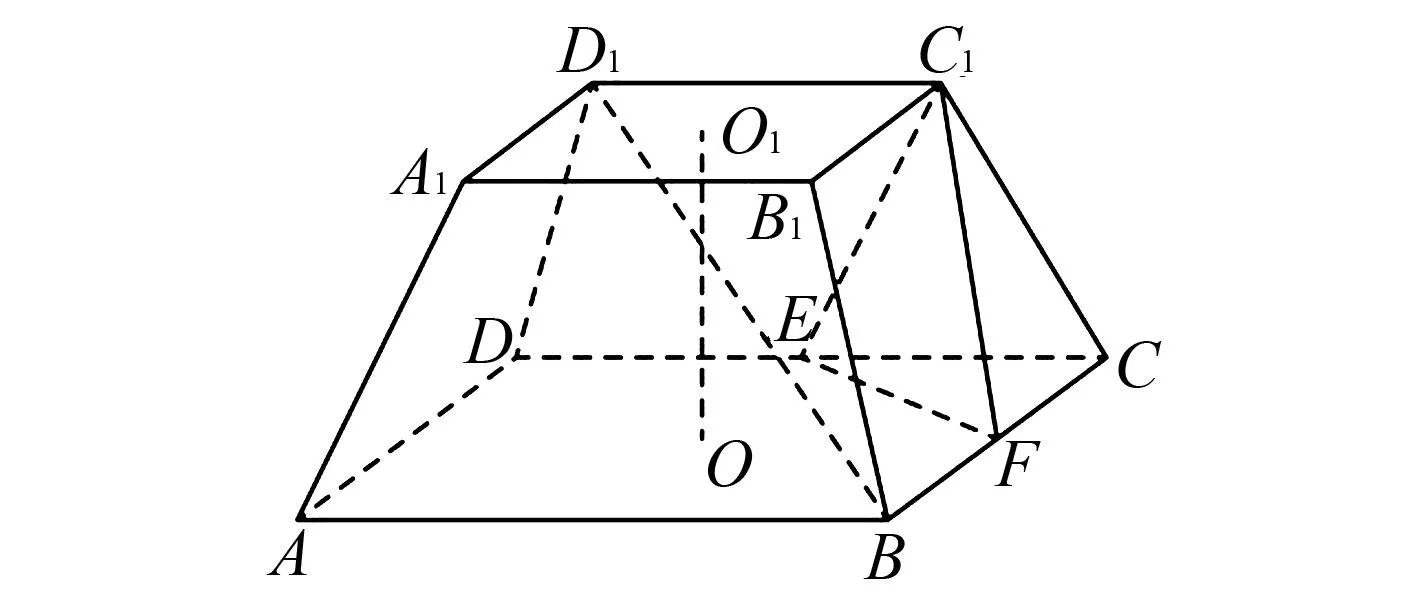
图3 第16题图

(1)求证:BD1∥平面C1EF;

(2)求点A1到平面C1EF的距离;

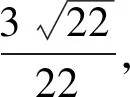
17.已知函数f(x)=ex-sinx-cosx,f′(x)为其导函数.

(1)求f(x)在[-π,+∞)上极值点的个数;

(2)若f′(x)≥ax+2-2cosx(a∈R)对∀x∈[-π,+∞)恒成立,求a的值.

18.设数列{an}的前n项和为Sn,已知a1=1,Sn+1-2Sn=1(n∈N*).

(1)求数列{an}的通项公式;

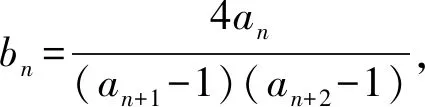
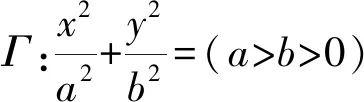
(1)求椭圆Γ的方程;

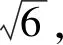
参考答案

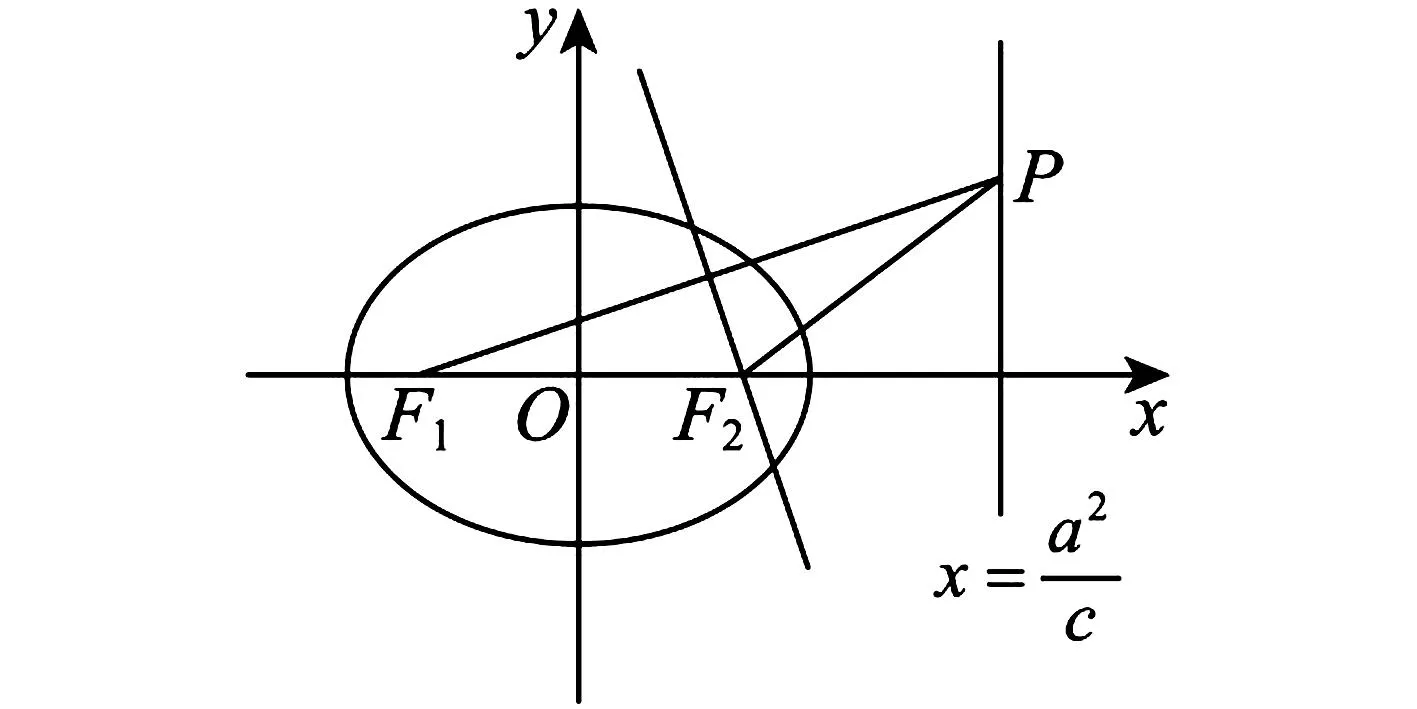
1.由题意得A={x|-2

故选A

3.若a=λb,则a与b共线,可知充分性成立;

若a与b共线,例如a≠0,b=0,则a=λb不成立,可知必要性不成立;

所以“a=λb”是“a与b共线”的充分不必要条件.

故选A.

4.因为函数f(x)=(x+a-2)(x2+a-1)为奇函数,所以f(0)=0.

即(a-2)(a-1)=0.即a=2或a=1.

显然函数f(x)=(x+a-2)(x2+a-1)的定义域为R关于原点对称,且当a=2时,f(x)=x(x2+1).

从而有f(-x)=-x(x2+1)=-f(x).

当a=1时,有f(x)=x2(x-1),但f(-1)=-2≠-f(1)=0,所以a=2,即f(x)=x(x2+1).

所以f(a)=f(2)=2×(22+1)=10.

故选D.

图4 第5题解析图

|PF2|=|F1F2|.

即3c4+2a2c2-a4≥0.

故选D.

6.由圆C:(x+1)2+(y-1)2=2,

解得k=1.此时l:y=x.

解得a=±2.此时l:x+y±2=0.

综上,如图5,共有3条满足条件的直线l.

图5 第6题解析图

故选C

7.由OA1=A1A2=A2A3=A3A4=A4A5=A5A6=A6A7=A7A8=…=2,

故选C.

故选B.

9.对于A,相关系数|r|≤1,且|r|越接近于1,相关程度越大,反之两个变量的线性相关性越弱,当-1≤r<0时,线性相关系数r越大,|r|则越小,线性相关性越弱,故选项A错误;

对于C:因为χ2=3.937>3.841=x0.05,所以有95%的把握可判断分类变量X与Y有关联,此推断犯错误的概率不大于0.05,故选项C正确;

故选BCD.

10.由题意可设f(t)=abt(ab≠0),

故A正确,B错误.

由于log32∈(0,1),故排气24分钟后,人可以安全进入车库,则C错误,D正确.

故选AD.

11.因为f(x)=(x2-x+1)ex定义域为R,且f′(x)=(x2+x)ex=x(x+1)ex,

令f′(x)>0,解得x<-1或x>0.

令f′(x)<0,解得-1

所以f(x)在(-∞,-1),(0,+∞)上单调递增,在(-1,0)上单调递减.

则f(x)在x=-1处取得极大值,在x=0处取得极小值,即f(x)有两个极值点,故A正确;

又f(1)=e,f′(1)=2e,所以f(x)在x=1处的切线方程为y-e=2e(x-1),即y=2ex-e,故B正确;

因为f(-1)=3e-1>1,f(0)=1,f(1)=e,所以f(x)在[-1,1]上的值域为[1,e],故C错误;

方程f(x)=a的解,即为y=f(x)与y=a的交点的横坐标.

所以f(x)=(x2-x+1)ex>0恒成立.

所以当a≤0时,y=f(x)与y=a没有交点,故D错误;

故选AB

13.因为三棱锥A-BCD的三条侧棱AB,AC,AD两两互相垂直,所以将三棱锥补成如图6所示的长方体,则长方体的体对角线等于三棱锥外接球的直径.

图6 第13题解析图

因为三棱锥外接球的表面积为25π,

所以AB2+AD2+AC2=(2R)2=25.

即3+6+AC2=(2R)2=25,解得AC=4.

又0°

所以∠A=60°.

图7 第16题解析图

设平面C1EF的一个法向量为n=(x,y,z),

令x=1,则n=(1,-1,0).

又因为BD1⊄平面C1EF,

所以BD1∥平面C1EF.

所以点A1到平面C1EF的距离为

设直线A1M与平面C1EF所成角为θ,

化简,得x2-35x+34=0.

则x=1或x=34(舍去).

即存在点M符合题意,此时BM=1.

又ex<1,所以f′(x)<0.

综上所述,f(x)在[-π,x0)上单调递增,在(x0,0)上单调递减,在[0,+∞)上单调递增.

所以f(x)在[-π,+∞)上仅有2个极值点.

(2)当x≥-π时,f′(x)≥ax+2-2cosx(a∈R)恒成立,即ex+sinx+cosx-ax-2≥0(a∈R).

令φ(x)=ex+cosx+sinx-ax-2,

若φ(x)≥0对∀x∈[-π,+∞)恒成立,

由φ(0)=e0+cos0-2=0,φ(x)≥0=φ(0),

所以当x=0时,φ(x)取得最小值.

由φ′(x)=ex-sinx+cosx-a,则x=0为函数φ(x)的极小值点,故φ′(0)=2-a=0,解得a=2.

下面证明:当a=2时,x=0为函数φ(x)的最小值点.

φ′(x)=ex-sinx+cosx-2,

令h(x)=ex-sinx+cosx-2,

则h′(x)=ex-cosx-sinx=f(x).

由(1)可知,f(x)在[-π,x0)上单调递增,在(x0,0)上单调递减,在[0,+∞)上单调递增.

又f(-π)=e-π+1>0,且f(0)=0,

所以当x≥-π时,f(x)的最小值为f(0)=0,则f(x)≥0恒成立.

即h′(x)≥0在[-π,+∞)上恒成立.

所以h(x)即φ′(x)在[-π,+∞)上单调递增.

又φ′(0)=0,所以当-π≤x<0时,φ′(x)<0,当x>0时,φ′(x)>0,所以函数φ(x)在[-π,0)上单调递减,在(0,+∞)上单调递增.

所以φ(x)≥φ(0)=0,即ex+sinx+cosx-2x-2≥0恒成立,符合题意.

综上所述,a=2.

18.(1)一方面:因为Sn+1-2Sn=1(n∈N*),

所以Sn+2-2Sn+1=Sn+1-2Sn=1(n∈N*).

所以Sn+2-Sn+1=2(Sn+1-Sn)(n∈N*).

即an+2=2an+1(n∈N*).

另一方面:当n=1时,有S2-2S1=1,即a2-a1=1,且a1=1,所以此时a2=2a1.

结合以上两方面以及等比数列的概念可知数列{an}是首项为a1=1,公比为q=2的等比数列.

故数列{an}的通项公式为an=1×2n-1=2n-1.

(2)由(1)可知an=2n-1.

又由题意

数列{bn}的前n项和为

而y1=2n+1-1关于n单调递增,

所以当n=1时,有

解得c=1.

(2)当直线AB的斜率存在时,设其方程为y=kx+m,由题意知m≠0.

(2+3k2)x2+6km+3(m2-2)=0.

此时有Δ=36k2m2-12(2+3k2)(m2-2)>0,

即3k2+2>m2.

(*)

设A(x1,y1),B(x2,y2),则有

又A,C关于原点对称,则C(-x1,-y1).

所以点C到直线AB的距离

所以△ABC的面积

整理,得3k2+2=2m2,符合(*)式.

因为3k2+2=2m2,所以m2≥1.