源于课本 提炼模型 灵活运用

张凤丽

(山东省泰安第三中学,山东 泰安 271000)

极化恒等式源自课本中的一道练习题,下面从这道题目谈起,提炼两种几何图形模型,并通过例题说明极化恒等式解题应用的灵活性及优越性.

1 源于课本

题目(人教A版普通高中教科书﹒数学必修第二册(2019年版)第22页练习第3题)[1]求证:(a+b)2-(a-b)2=4a·b.

简证左边=(a2+2a·b+b2)-(a2-2a·b+b2)=4a·b=右边.故等式得证.

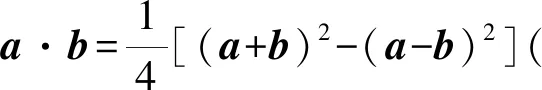
我们把这一公式称之为极化恒等式,它反映了两个非零向量的数量积与它们的和及差之间的等量关系,三个量可知二求一.

2 提炼模型

极化恒等式主要用来求解共起点向量的数量积问题,可从几何图形模型提炼出三角形模型以及平行四边形模型.

2.1 三角形模型

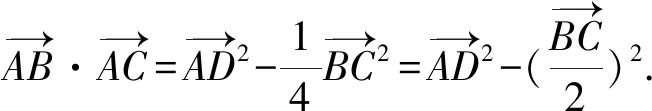
图1 三角形模型示意图

证明因为D为△ABC的边BC的中点,

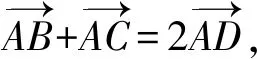
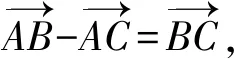
根据极化恒等式,则

文字诠释三角形相邻两边向量的数量积等于第三边中线向量的平方与第三边向量一半的平方的差.简记为:数量积等于中线方减去底半方.

推论2(三角形中线长定理)如图1,在△ABC中,D是BC的中点,则

2.2 平行四边形模型

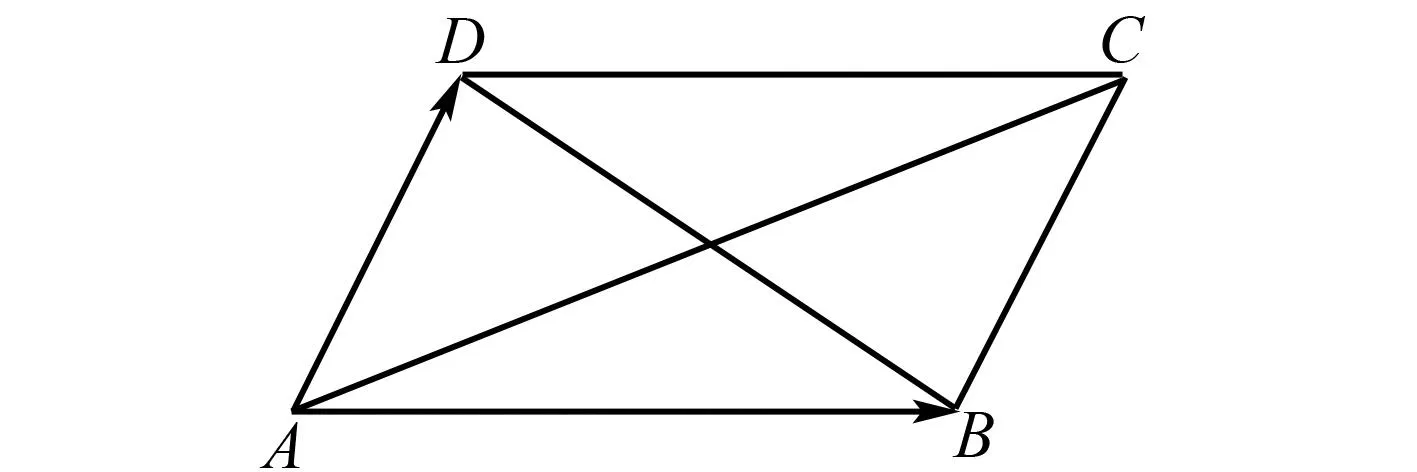
图2 平行四边形模型示意图

证明在ABCD中,

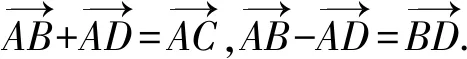
根据极化恒等式,则

3 灵活运用

极化恒等式把两个非零向量数量积化归为它们和向量与差向量平方差的四分之一,因此当和向量与差向量都为已知时,可以运用极化恒等式求解,尤其是求解含有中点或能构造中点的两个共起点向量的数量积问题时,运用极化恒等式或它的几何模型解答可达到事半功倍之效.

3.1 求数量积

解析因为D是BC的中点,所以由极化恒等式的三角形模型,得

点评若运用基底法和坐标法解答本题,求解过程运算量大,过程复杂.这里根据D是BC的中点的题设条件,直接运用极化恒等式的三角形模型求解,则求解十分快速、简捷.

3.2 求数量积的取值范围

A.[-3,1] B.[-1,3]

C.[-4,2] D.[-2,6]

解析如图3,取AB中点D,连接CD.

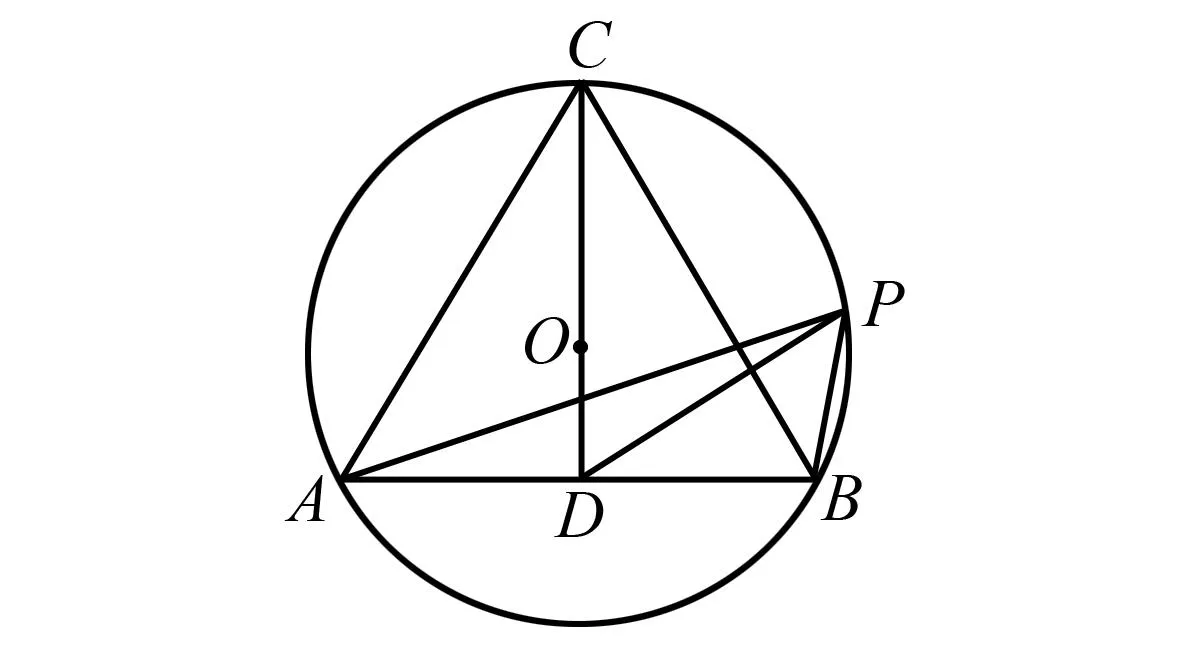
图3 例2题图

因为△ABC为正三角形,所以O为△ABC的重心,O在CD上,且OC=2OD=2.

所以CD=OC+OD=3,

根据极化恒等式的三角形模型,得

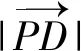
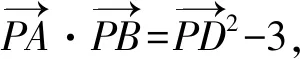
3.3 求数量积的最值

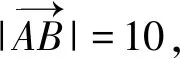
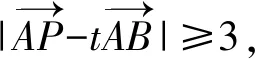
所以由三角形模型极化恒等式得

≥9-25=-16,

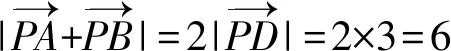
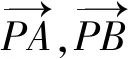
3.4 其他应用

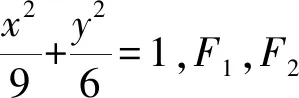
解析根据椭圆定义,得

|PF1|+|PF2|=2a=6.

①

在△F1PF2中,由余弦定理,得

|PF1|2+|PF2|2-2|PF1||PF2|cos∠F1PF2=|F1F2|2,

由三角形模型极化恒等式推论,得

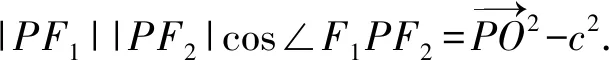
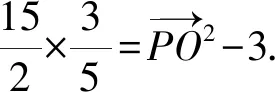
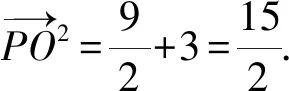
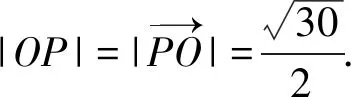
4 结束语

通过上述题目可以看出,极化恒等式能够有效地建立起数量积与几何图形中长度大小的联系,是连接代数与几何之间的桥梁和纽带.对于那些共起点且与中点相关联的向量数量积运算问题,灵活运用极化恒等式是一条颇为有效的途径.