对一道线段比值为定值问题的深入探究——以2023年3月清华中学生标准能力测试第21题为例

王东海

(安徽省合肥市肥东县城关中学,安徽 合肥 231600)

高中新课标突出对学生数学核心素养的考查,而圆锥曲线成为考查逻辑推理能力和数学运算的重要载体.其中有关“定”的问题在高考和模考中频繁出现,主要包括了动直线过定点,证明线段长、面积、斜率和积、线段比值为定值等问题.定值问题的特征是“定”,而与“定”相对的是“动”,因而定值问题的本质就是寻找运动变化过程中的不变性.正如张奠宙教授所言:数学中到处都是变与不变的矛盾统一,数学研究变化,却以找到其中的不变性作为归宿.寻找并欣赏数学中无处不在的不变性质,领略不变量和不变性的内在魅力,是把握数学的钥匙之一.下面以2023年清华中学生能力测试第21题为例进行探究.

1 考题呈现

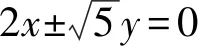
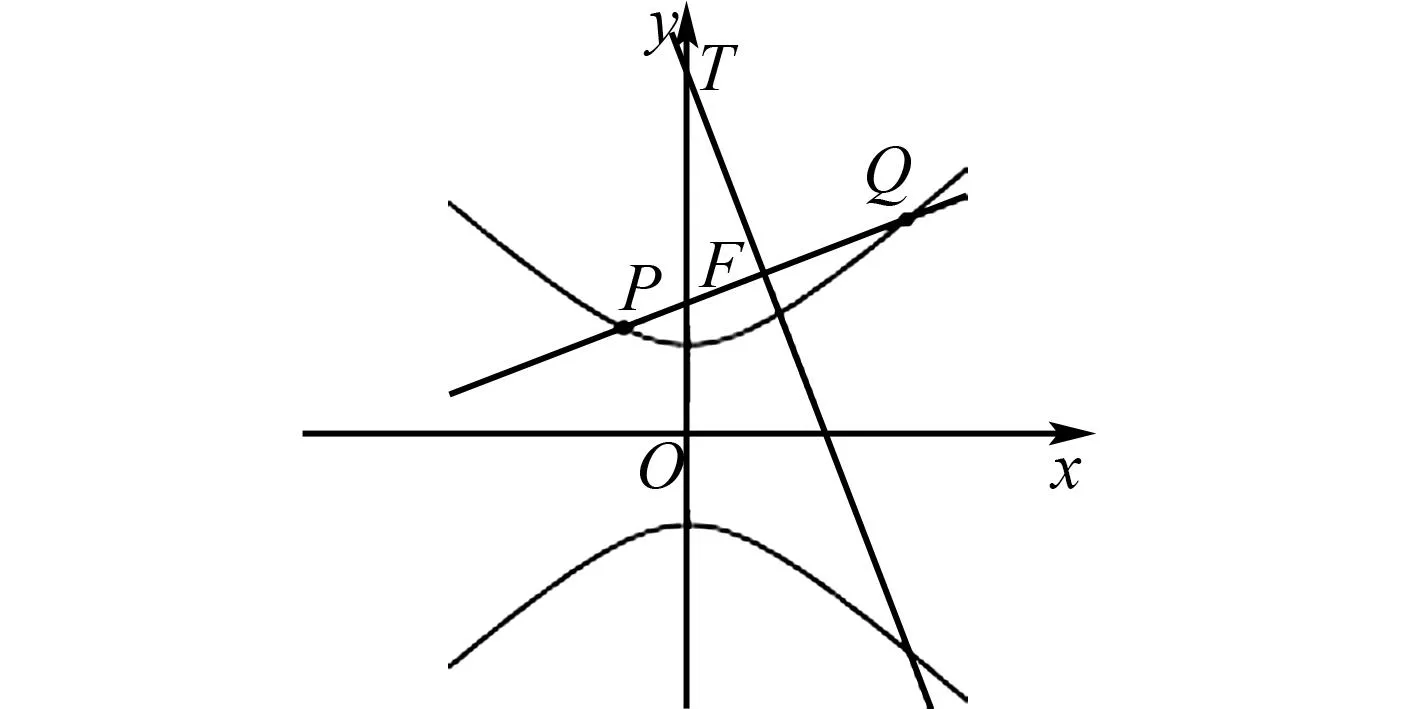
图1 2023年清华中学生能力测试第21题

(1)求双曲线C的方程;

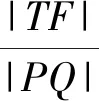
分析该题考查了双曲线的标准方程、几何性质、直线与圆锥曲线的位置关系以及线段定值问题,检验学生分析问题和解决问题的能力,也考查了学生数学运算、逻辑推理、直观想象等数学核心素养.考题设计精巧、内涵丰富,是一道有研究价值的好题.

2 解法探究

视角1 本题通解是直曲联立结合设而不求思想,分别求两条线段的长度,再消去参数即可.

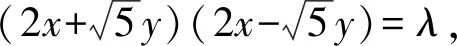
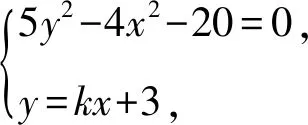
5(kx+3)2-4x2=20.

化简,得(5k2-4)x2+30kx+25=0.

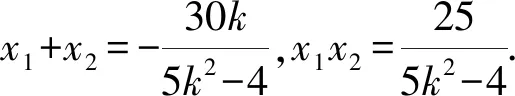
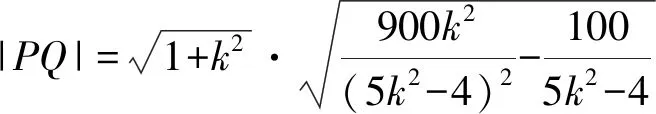
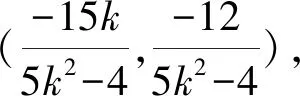
所以PQ中垂线方程为

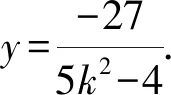
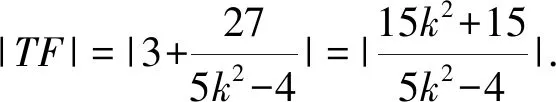
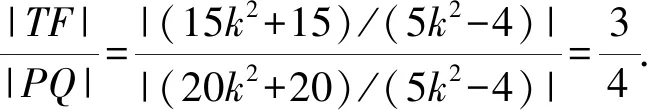
视角2 考虑分子是焦点弦长,故使用焦半径公式.分母可用点差法或垂径定理处理,从而无需直曲联立来解决,这样可以节约运算量.

解析2设P(x1,y1),Q(x2,y2),PQ中点为(x0,y0),故由双曲线的焦半径公式可得:

|PQ|=|FP|+|FQ|=(ey1-a)+(ey2-a)=e(y1+y2)-2a=3y0-4.

又因P,Q均在双曲线上,故

两式相减,得

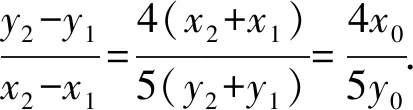
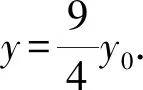
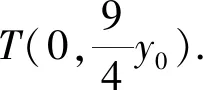
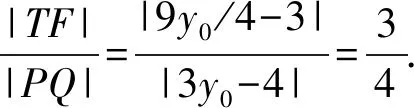
视角3 考虑到直线l过定点F,故而可考虑直线的参数方程,利用其几何意义处理该题.

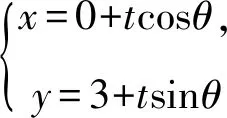
5(3+tsinθ)2-4(tcosθ)2-20=0.

整理知(5sin2θ-4cos2θ)t-30sinθ·t+25=0.

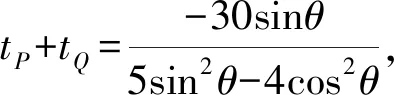
所以|PQ|=|tP-tQ|

①

又PQ中点M对应的

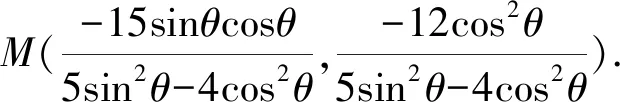
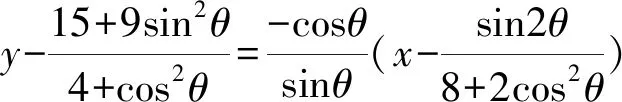
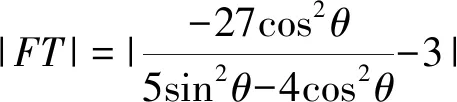
②

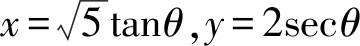
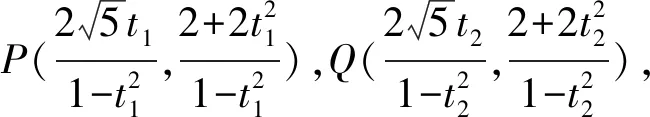
即(t1-t2)(1+t1t2)=0.

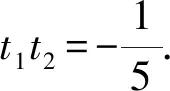
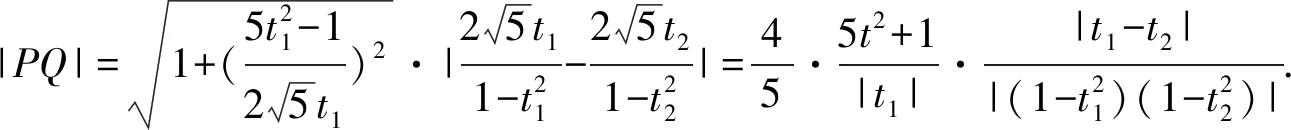
③

又因PQ中点M为

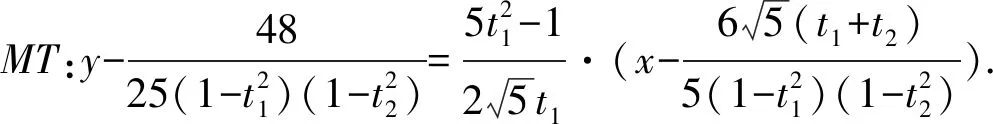
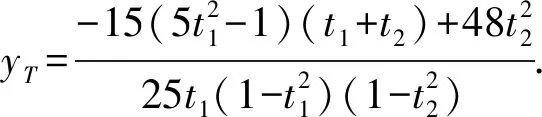
④

从而将③④代入比值式得

3 一般性推广

波利亚曾说:“没有任何一个题目是彻底完成了的,总还会有些事情可以做.[1]”细品解题过程及结论,笔者发现第(2)问的解答耐人寻味,值得探究.于是笔者思考,当双曲线为特殊的5y2-4x2=20时,线段TF和PQ比值为定值,那么对于一般双曲线b2y2-a2x2=a2b2,线段TF和PQ比值是否仍为定值?当双曲线焦点在x轴时呢?另外能否类比到椭圆和抛物线呢?进一步还能推导出哪些拓展结论呢?基于以上思考,笔者探究得到如下结论:

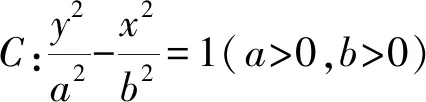
可以联想到,将焦点在y轴上的双曲线顺时针旋转90°,则可得到相似结论:

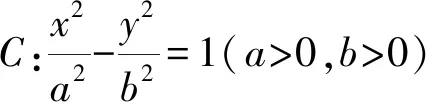
证明设P(x1,y1),Q(x2,y2),PQ中点(x0,y0),因直线l过点F,故设l:y=k(x-c),与已知双曲线b2x2-a2y2=a2b2联立,消去y,得

(b2-a2k2)x2+2a2ck2x-a2c2k2-a2b2=0.

故由弦长公式,得

⑤

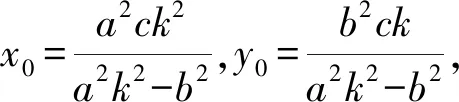
所以线段PQ的中垂线方程为

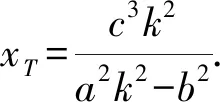
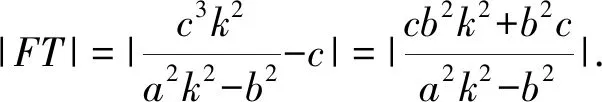
⑥

结论1证法类似结论2,这里略.

再由特殊到一般的探究思路,假如将直线l所过定点F推广到y轴上一般的定点N(0,n),其他条件不变,那么线段NT和PQ的比值是否仍为某定值呢?

这里仍以双曲线b2y2-a2x2=a2b2为例,联立l:y=k(x-n)和b2y2-a2x2=a2b2消去y,可由韦达定理和弦长公式得

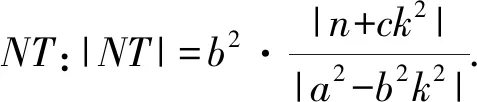
从而知

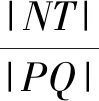
另外还可探究当点M为线段PQ的三等分点或其他等分点时,两线段比值是否为定值?

碍于篇幅,这里略.

4 类比推广

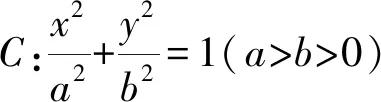
结论1和结论3的证法类似于结论2,这里略.

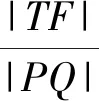
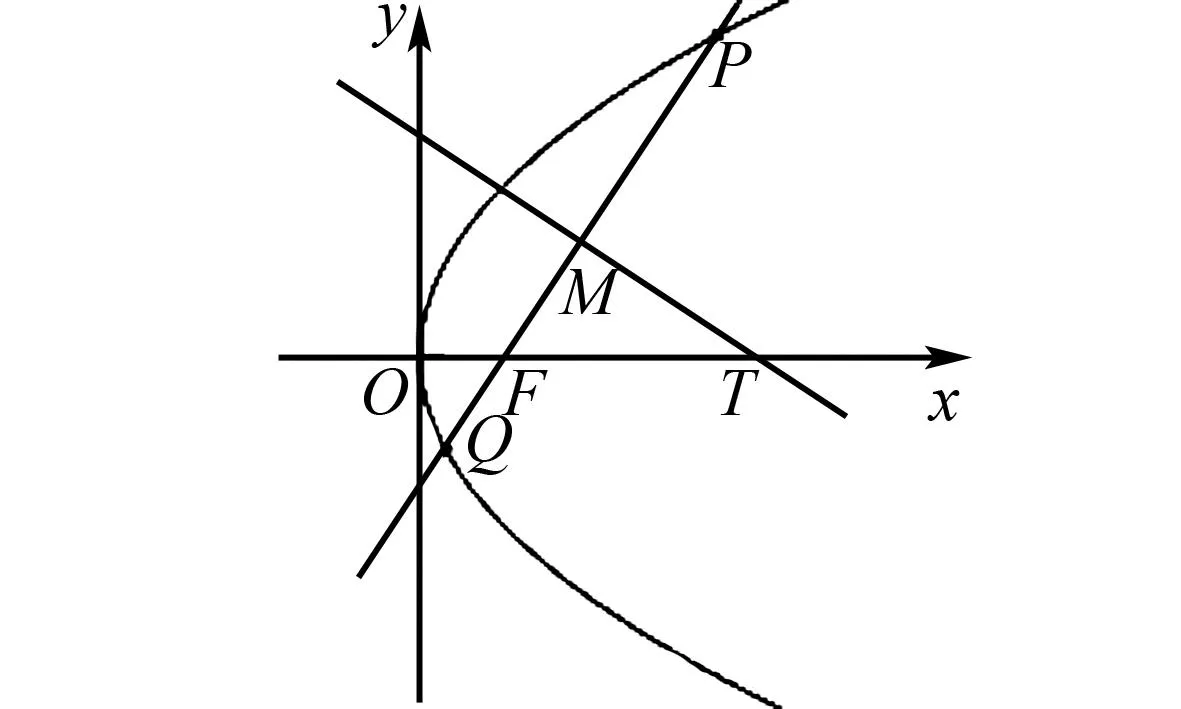
图2 结论4几何图

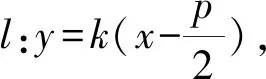
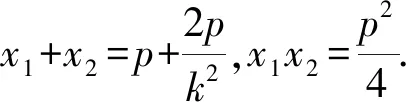
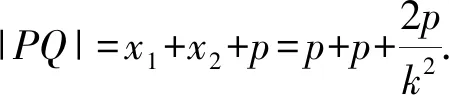
⑦

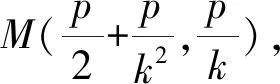
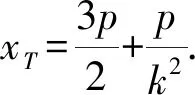
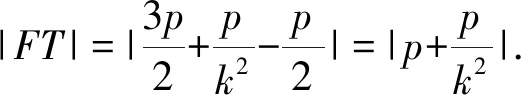
⑧

对于抛物线我们还可以进一步进行拓展,得到一些更深入的结论,这对于掌握此类问题的性质和培养学生的探究意识大有裨益.

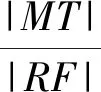
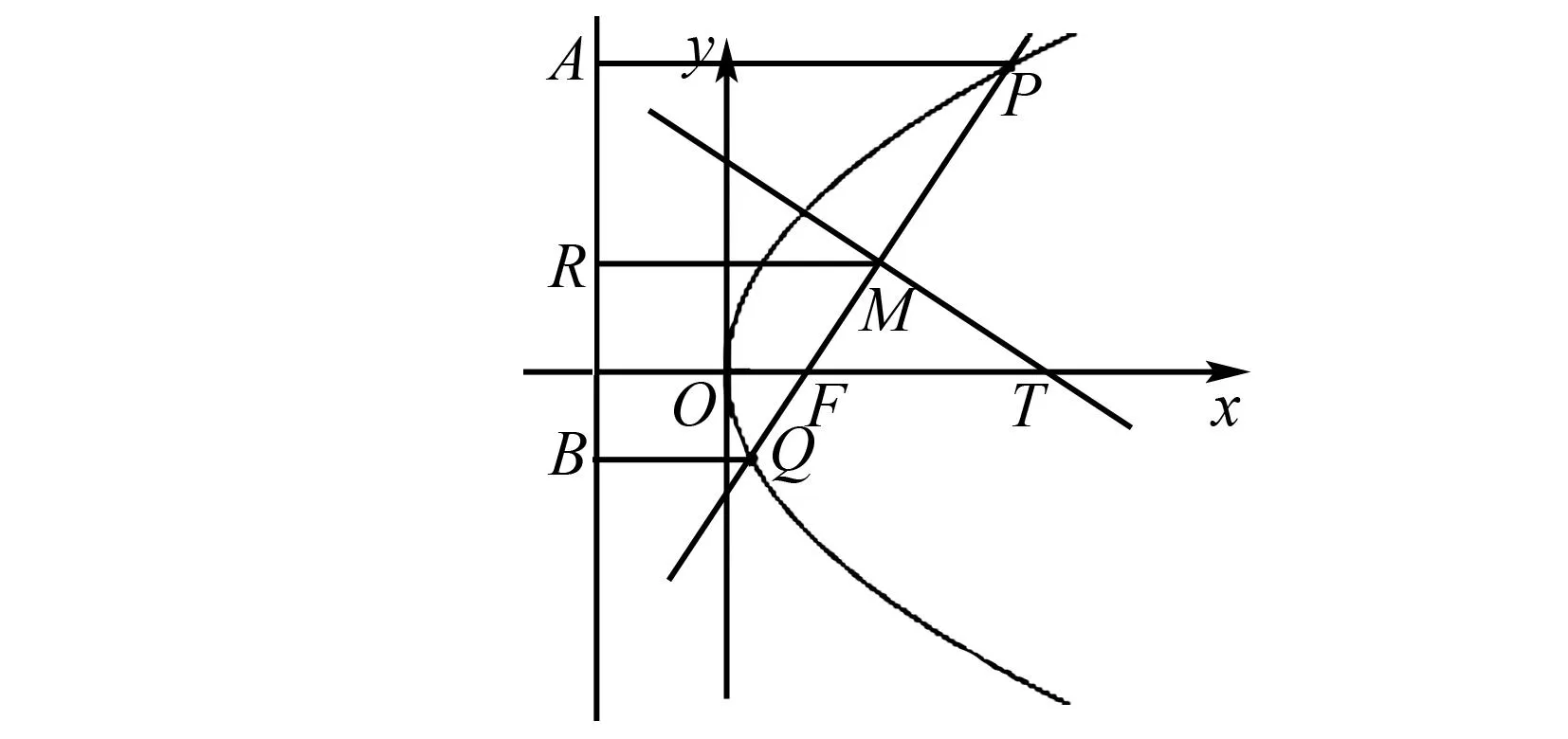
图3 结论5几何图

证明因MR∥FT,而由结论4知

又线段MR的长度

所以|MR|=|FT|.

从而四边形MRFT为平行四边形.

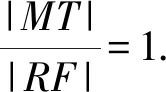
结论6 一般地,抛物线C:y2=2px(p>0)的焦点为F,不平行于y轴的直线l过点F与抛物线C交于P,Q两点,PQ的中垂线交x轴于点T,过P,Q两点作准线的垂线,垂足分别为A,B,若AB的中点为R,PQ的中点为M,则RF⊥PQ且线段RM中点在C上[3].

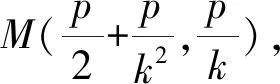
另外,我们还可探究对于椭圆和双曲线是否有类似结论,感兴趣的读者可进一步进行探究.

5 结束语

由特殊到一般是数学研究的一种常用方法.教师在实际教学中,在解决这些特殊问题后如能加以深入思考和探究,则必能从一类题型拓展到一种方法,由掌握一种方法到解题能力的提升,最终能够将这种能力化为学生的数学素养.