确定圆锥曲线的轨迹方程中范围的策略

李文东

(广东省中山市中山纪念中学,广东 中山 528454)

求曲线的轨迹方程问题是解析几何的两个基本问题(求曲线轨迹方程问题和根据方程研究曲线的性质)之一.求轨迹方程的方法很多[1],相对比较容易掌握,本文不再探讨求轨迹方程的方法.在求轨迹方程时,同学们面对的难点是轨迹方程中的变量取值范围的确定,即轨迹方程的纯粹性,这需要我们全方面、细致地考虑问题.本文探讨此类问题的常见思考策略.

1 根据代数式、方程本身的意义或范围确定轨迹的范围

求轨迹方程时要考虑曲线本身的范围或代数式的意义(比如斜率公式的分母不能为零).

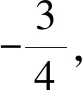
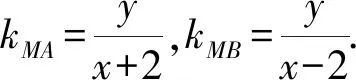
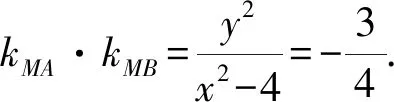
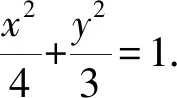
为保证斜率存在,则x≠±2.

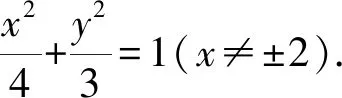
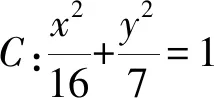
解析设M(x,y),P(x,y0),点P在椭圆C上,

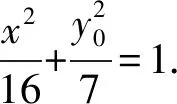
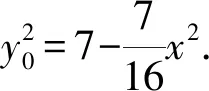
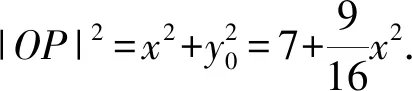
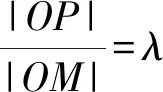
整理,得(16λ2-9)x2+16λ2y2=112.

由于点P在椭圆C上,故x∈[-4,4].

于是点M的轨迹方程为

(16λ2-9)x2+16λ2y2=112,x∈[-4,4].

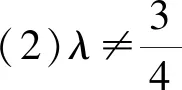
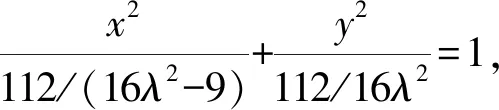
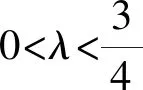
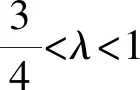
当λ≥1时,点M的轨迹为中心在原点、长轴在x轴上的椭圆.

2 根据图形中的特殊情形(特殊点、特殊位置)确定轨迹的范围

在求轨迹方程时,需要考虑几何图形中的一些特殊情形,比如三角形的三个顶点不共线、双曲线的渐近线对双曲线的影响等.

例3 已知△ABC的顶点A(-3,0),B(3,0),若顶点C在抛物线y2=6x上移动,求△ABC的重心的轨迹方程.

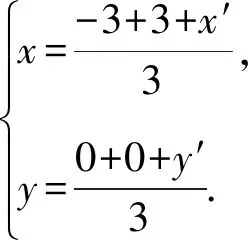
因为点C在曲线y2=6x上,所以有(3y)2=6×3x,即y2=2x.

因为三角形的三个顶点不能共线,所以y≠0.

故△ABC的重心的轨迹方程为y2=2x(y≠0).

点评本题是典型的相关点法求轨迹方程,题目中三点A,B,C要构成三角形,因此三个顶点不能共线,这就对轨迹方程产生范围.

例4 圆x2+y2=4,A(-1,0),B(1,0),动抛物线过A,B两点,且以圆的切线为准线,则抛物线的焦点轨迹方程为____.

解析根据抛物线的定义,焦点F到A和B的距离之和等于A和B分别到准线的距离和.如图1,点A和B到准线的距离分别为|AM|,|BN|,点O到准线的距离为|OP|,由梯形的中位线知|AM|+|BN|=2|OP|=2r=4.

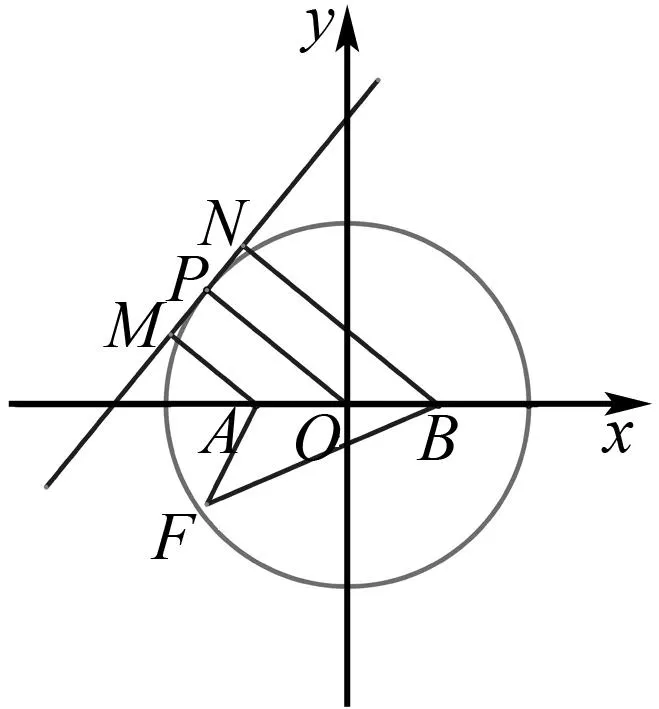
图1 例4解析图

故|FA|+|FB|=4.

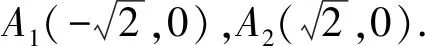
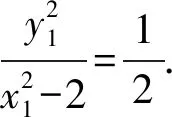
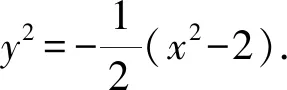
由于点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点,当点P为左、右顶点A1,A2时,P,Q重合,此时直线A1P与A2Q交点也为左、右顶点A1,A2,不符合题意;

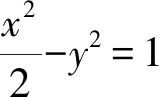
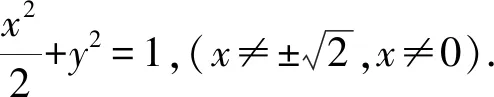
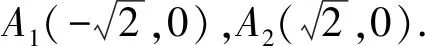
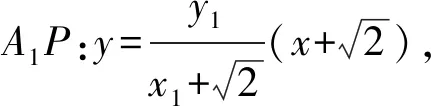
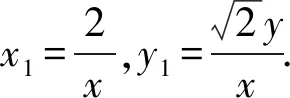
①

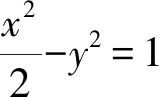
下面根据求解过程确定轨迹方程的范围:

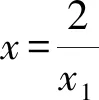
3 根据几何图形的特征确定轨迹的范围

一些轨迹问题中,由于题中几何图形的特征,轨迹往往被限制在某部分,这时需要先作出题中的几何图形,然后细致观察轨迹的大概分布情况.

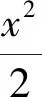
解析设弦两端点分别为M(x1,y1),N(x2,y2),线段MN的中点R(x,y),则

①-②,得

(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0.

由题意知x1≠x2,则上式两端同除以x1-x2,有

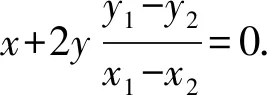
⑤

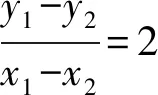
x+4y=0.

显然中点在椭圆内,故所求轨迹方程为

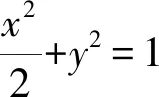
例7求与⊙C1:x2+(y-1)2=1和⊙C2:x2+(y+1)2=4都外切的圆的圆心M的轨迹方程.

解析设动圆M的半径为r,因为⊙M与⊙C1,⊙C2都外切,所以|MC1|=r+1,|MC2|=r+2.

所以|MC2|-|MC1|=1.

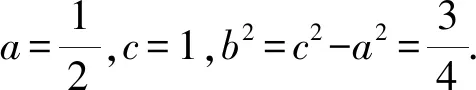
所以所求的双曲线的方程为

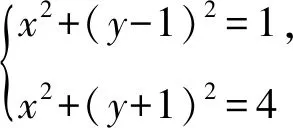
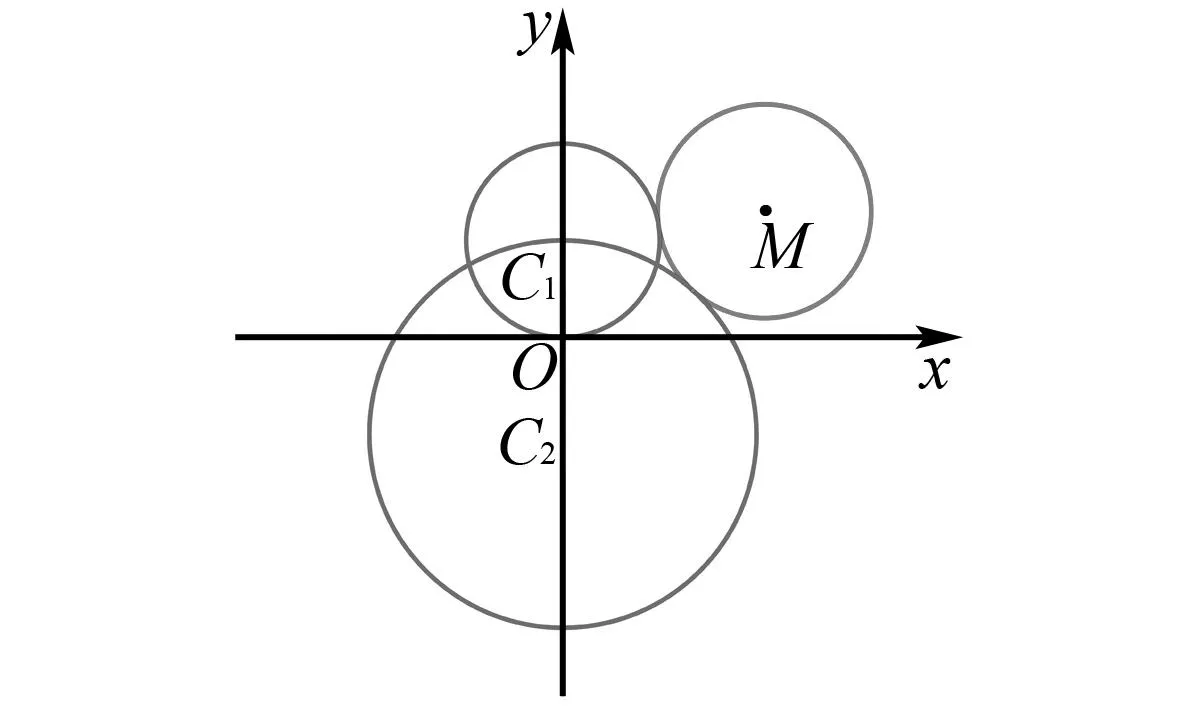
图2 动圆外切图

例8已知圆F1:x2+y2+4x=0,圆F2:x2+y2-4x-12=0,一动圆与圆F1和圆F2同时内切.求动圆圆心M的轨迹方程.

错解由圆F1:x2+y2+4x=0,得

(x+2)2+y2=4.

可知F1(-2,0),其半径为2.

由圆F2:x2+y2-4x-12=0,得

(x-2)2+y2=16,

可知F2(2,0),其半径为4.

设动圆半径为r,

圆M与圆F1和圆F2同时内切,

故|MF1|=r-2,|MF1|=r-4.

于是|MF1|-|MF2|=2<|F1F2|=4.

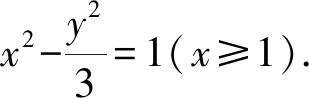
上述解法是不完整的,原因是没有结合具体图形的位置考虑,需要画出图形,仔细观察求解.

解析如图3,需要分两种情形讨论:

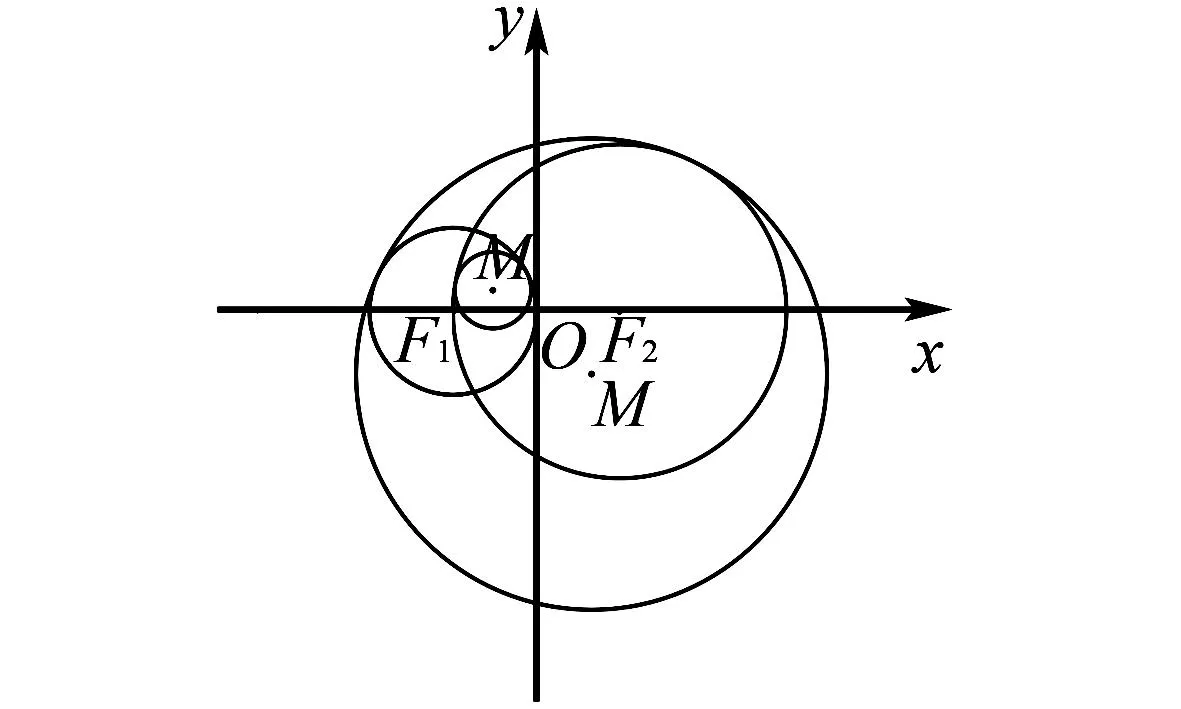
图3 动圆内切和外切图

由圆F1:x2+y2+4x=0,得(x+2)2+y2=4,

可知F1(-2,0),其半径为2.

由圆F2:x2+y2-4x-12=0,得

(x-2)2+y2=16,

可知F2(2,0),其半径为4.

设动圆半径为r,

(1)当动圆M在圆F1,F2外面时:

|MF1|=r-2,|MF1|=r-4,

故|MF1|-|MF2|=2<|F1F2|=4.

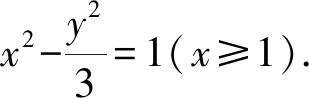
(2)当动圆M在圆F1,F2里面时:

|MF1|=2-r,|MF1|=4-r,

故|MF2|-|MF1|=2<|F1F2|=4.

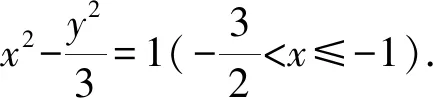
综上,动圆圆心M的轨迹方程为

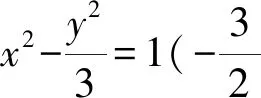
4 结束语

在求解轨迹问题时,需要考虑轨迹方程的纯粹性和完备性,这可以培养学生的逻辑推理能力和思维的严密性.对于轨迹方程的纯粹性,要结合代数式、方程本身的意义或范围、图形中的特殊情形(特殊点、特殊位置)和几何图形的特征来细致考虑.