两类弹簧木板分离问题比较探究

杨天才

(重庆市大学城第一中学校,重庆 401331)

弹簧木板分离问题是高中物理中的重要临界模型,是力学板块的难点知识,含弹簧的问题也是高频考点.弹簧木板分离问题涉及的过程多,处理该问题所用的规律、公式复杂,不易理解,导致学生在考试中容易失分.这就需要学生学习时对这类现象及规律进行浸润式思维,深刻领会物理概念、规律的本真,深度学习,不断提升核心素养.因此,弄清两类典型模型的特点,掌握应用相应规律的方法,熟悉应用模型去解决实际问题很有必要.为此,本文将对弹簧木板分离前一起做匀加速运动和简谐运动进行分析和探讨,以求达到掌握其特点并熟练应用的目的[1-2].

1 模型分类

如图1所示,一根劲度系数为k的轻质弹簧一端固定在水平面上,另一端与滑块B相连,滑块A与B靠在一起(不粘连),两滑块的质量分别为mA、mB,系统处于静止状态,弹簧始终在弹性限度范围内,从零时刻起对滑块A施加一个竖直向上的力F作用.

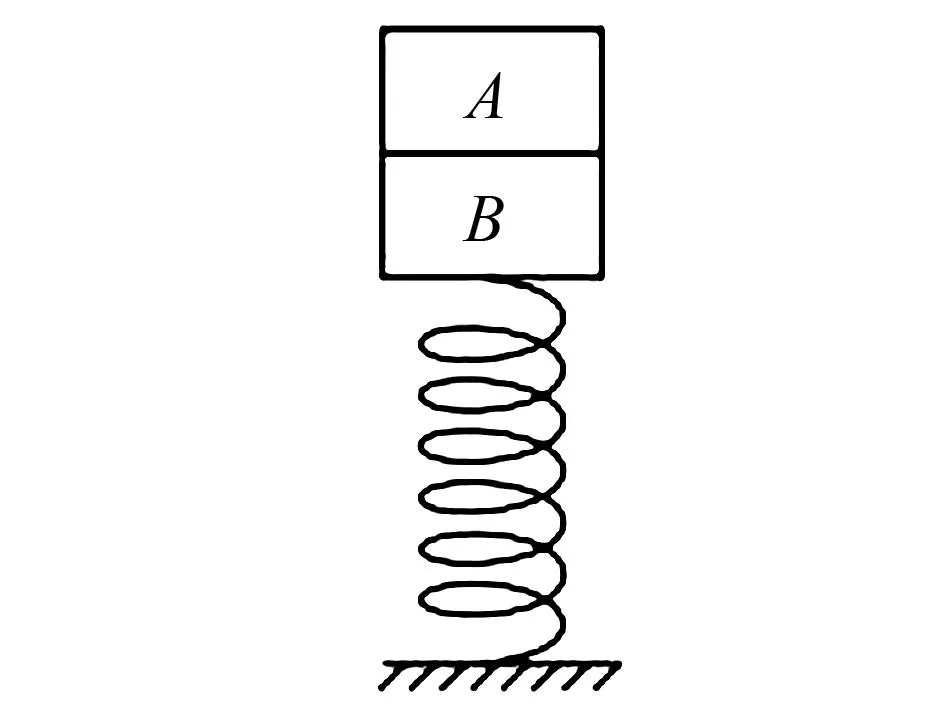
图1 题目示意图

1.1 匀加速运动(F是变力)

滑块A与B向上一起匀加速直线运动,设匀加速运动的加速度已知为a.则:

运动性质:分离前二者一起做匀加速直线运动,分离后A做匀变速直线运动,B做简谐运动.

外力变化:分离前变力,分离后是恒力.

分离临界条件:二者加速度、速度相等,相互作用力为零.

分离前(含分离时)满足的物理规律:如图2所示,初始时刻,对整体,由力的平衡条件,有:

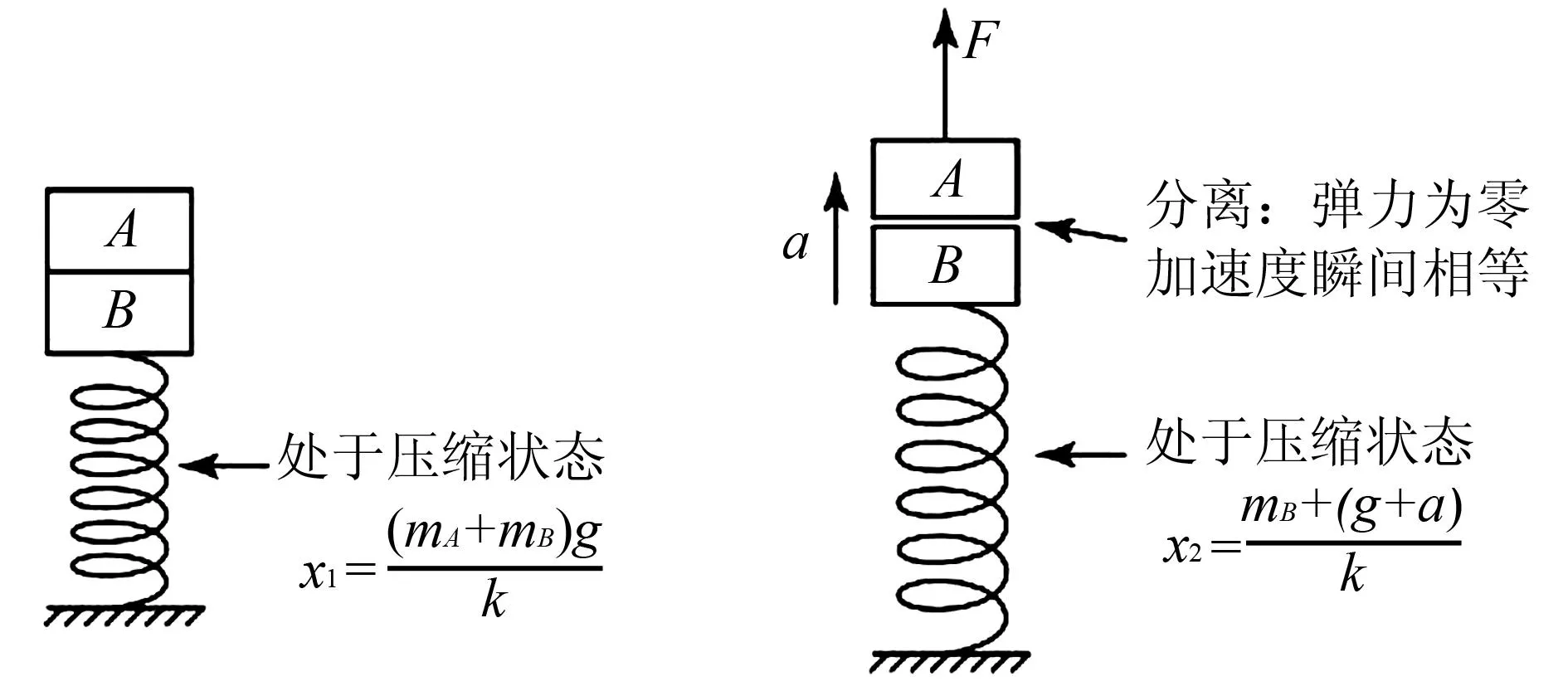
图2 弹簧木板在初始与分离时刻状态图

kx1=(mA+mB)g

①

分离时,对滑块B,由牛顿第二定律,有:

kx2-mBg=mBa

②

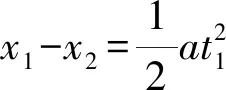
③

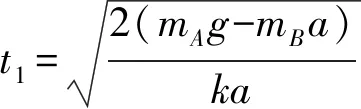
④

在匀加速过程中,设整体的位移为x,有:

F+k(x1-x)-(mA+mB)g=(mA+mB)a

⑤

成立,变形得:F=kx+(mA+mB)a

⑥

函数图像如图3所示.且当x=0时,拉力取最小值,有:

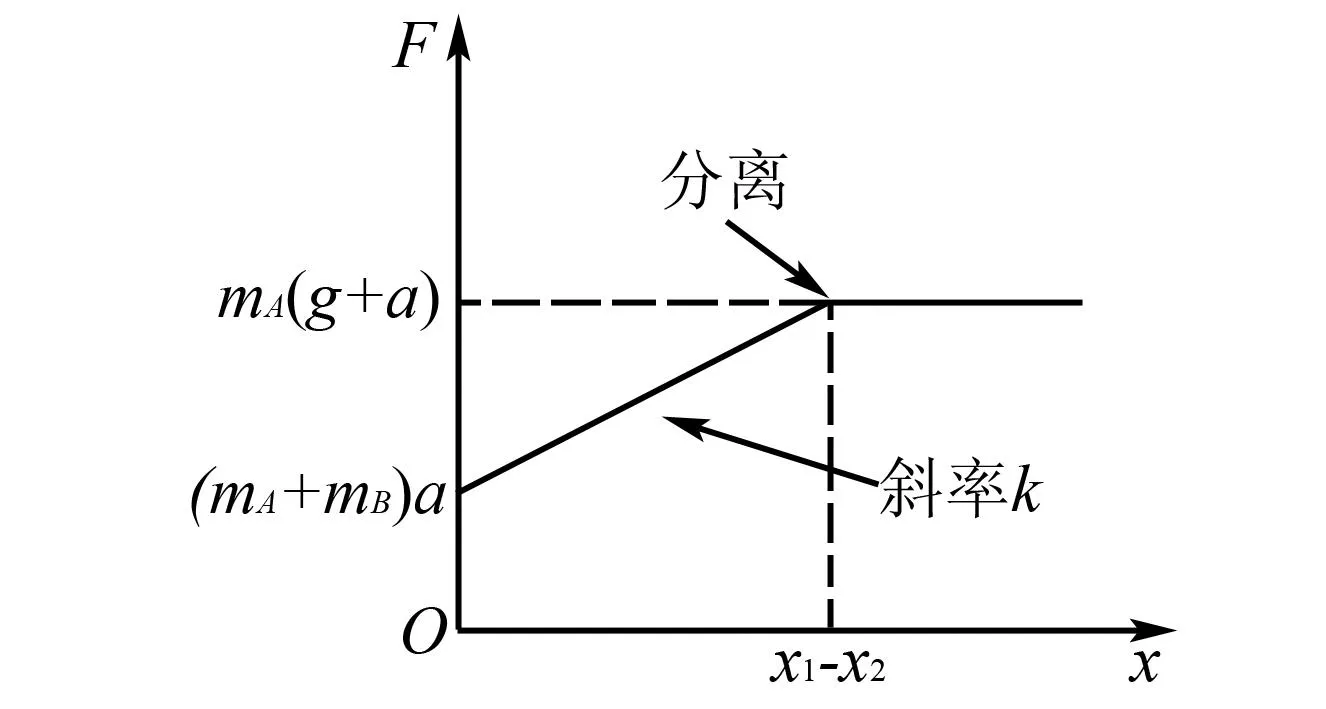
图3 力与位移的函数图像

Fmin=(mA+mB)a

⑦

当x=x1-x2时,拉力取最大值,有:

Fmax=mA(g+a)

⑧

由运动学公式,得:v=at1

⑨

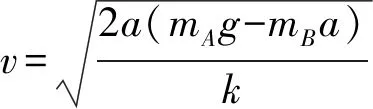
⑩

v-t图像如图4所示.由于在F-x图像中,图线与x轴所围“面积”在数值上表示力F在这段位移所做的功,由图3可知,外力所做的功为:

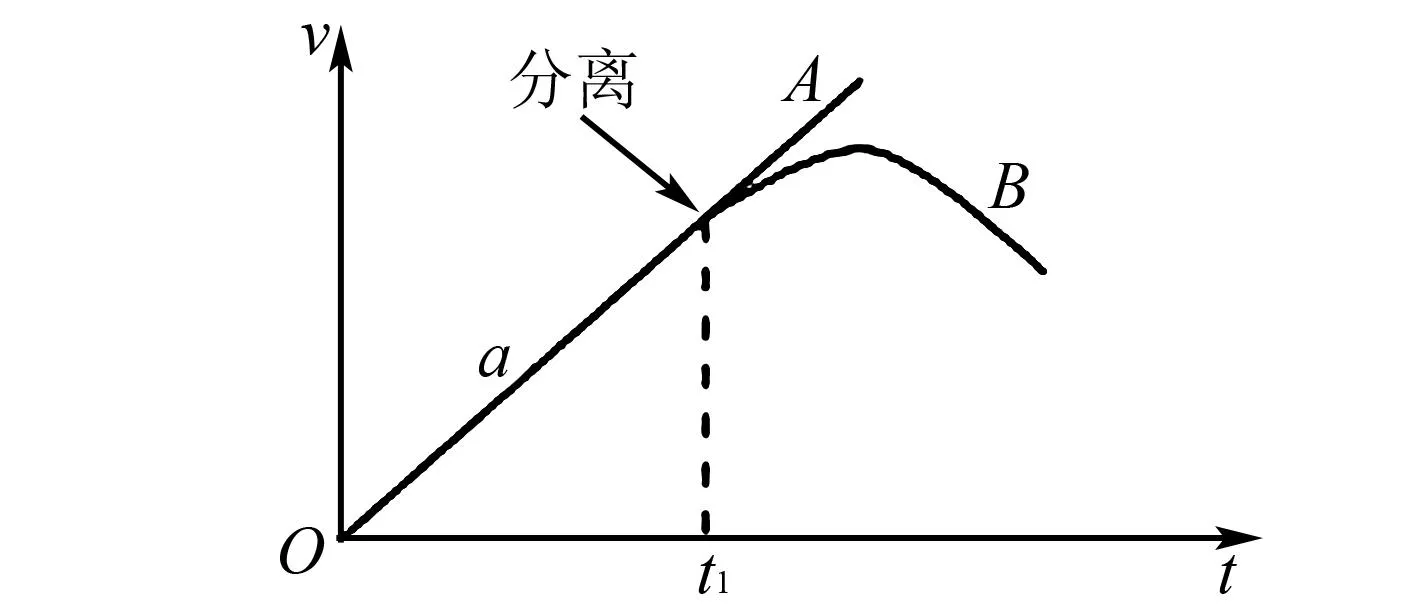
图4 速度与时间图像

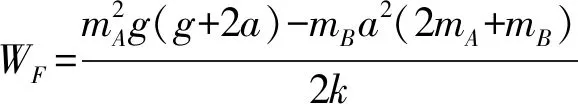
对整体,由动能定理,得:

WF+[-(mA+mB)g(x1-x2)]+W弹

弹簧弹力所做的功为:

W弹=-ΔEP弹

1.2 简谐运动(F是恒力)

A与B向上一起简谐运动,已知竖直向上的拉力为F.则:

运动性质:分离前二者一起做简谐运动,分离后滑块A做匀变速直线运动,滑块B做简谐运动.

分离临界条件:二者加速度、速度相等,相互作用力为零.

是否分离的条件及规律:初始位置,对整体,由力的平衡条件,有:kx1=(mA+mB)g

①

设振幅为A,此时在F的作用下二者的加速度最大且满足:F=kA=(mA+mB)amax

②

若在滑块B运动的最高点分离,由对称性,对滑块A,有:mAg-F=mAamax

③

对滑块B,满足:mBg-kx2=mBamax

④

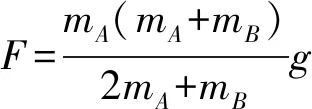
⑤

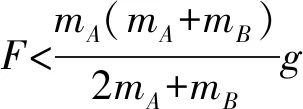
⑥

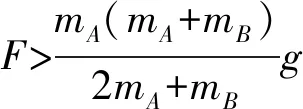
⑦

二者一定会分离;且分离时弹簧的压缩量

⑧

平衡位置:设二者做简谐运动的平衡位置对应弹簧的压缩量为x3,由对称性,则振幅

A=x1-x3=x3-x2

⑨

且F+kx3=(mA+mB)g

⑩

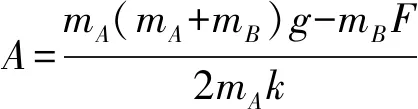
函数图象:若不分离,v-t图像为标准的正弦函数.

2 应用品鉴

例1 如图5(a)所示,光滑斜面的倾角为30°,一根轻质弹簧一端固定在斜面底端,另一端与滑块A相连,滑块B与A靠在一起(不粘连),两滑块的质量均为m,系统处于静止状态.从零时刻起对滑块B施加一个平行斜面的变力F,两滑块的v-t图像如图5(b)所示,t0时刻F的大小是零时刻F大小的2倍,重力加速度大小为g,弹簧始终处于弹性限度内,则下列说法正确的是( ).

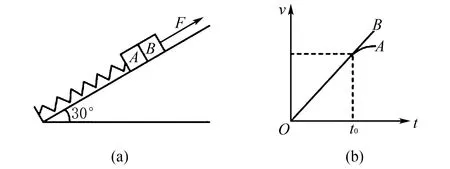
图5 题目示意图与速度时间图像

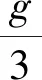
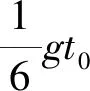
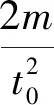
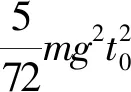
解析由图5(b)所示图像可知,t=t0时刻两滑块开始分离,此时它们的加速度大小、速度大小分别相等,它们间的作用力为零,设此时弹簧的压缩量为x,设t=0时弹簧的压缩量为x0,弹簧的劲度系数为k,则t0时刻拉力大小为2F0,施加拉力前,对A、B整体,由平衡条件得:kx0=2mgsin30°

①

t=0时刻,对A、B整体,由牛顿第二定律得:

F0+kx0-2mgsin30°=2ma

②

t0时刻,对滑块B,由牛顿第二定律得:

2F0-mgsin30°=ma

③

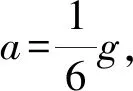
④

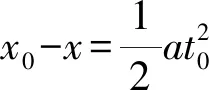
⑤

t0时刻,对滑块A,由牛顿第二定律得:

kx-mgsin30°=ma

⑥

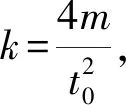
⑦

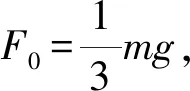
⑧

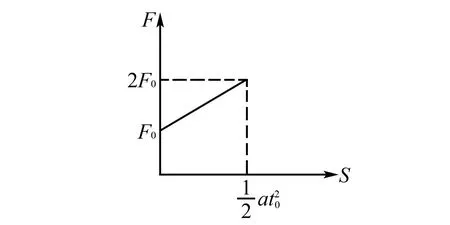
图6 力与位移函数图像

设弹簧弹性势能的减少量为EP,则根据功能关系,F做功与弹簧弹性势能的减少量之和等于系统重力势能与动能的增加量,即

⑨

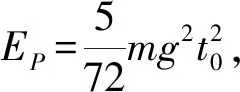
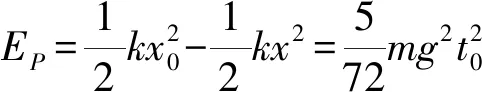
⑩

选项D正确.

3 结束语

弹簧木板分离问题本质还是弹簧的临界问题[3],对学生物理核心素养要求较高.弹簧问题几乎在每年的高考试题中都有所体现,解决弹簧问题的关键是画出物体运动的情境图,然后进行正确的受力分析、运动过程分析、做功分析、能量分析、冲量分析、动量分析[4].