平面一般二次曲线的垂径定理及其应用

钟德光 肖柔敏

(1.深圳职业技术大学应用数学研究中心,广东 深圳 518055;2.广东金融学院金融数学与统计学院,广东 广州 510521)

垂径定理是圆的一个重要性质,它在椭圆、双曲线以及抛物线都有类似的推广.目前为止,中小学数学关于椭圆、双曲线以及抛物线的垂径定理的讨论都是零散的,因此,寻找圆锥曲线的垂径定理的统一形式有着重要意义.

1 圆的垂径定理及其在圆锥曲线中的推广

命题1设O是坐标原点,且设直线l与圆O相交于A,B两点,点D为线段AB中点.在直线OD的斜率存在且不为零的情况下,则有

kOD·kAB=-1.

圆的上述解析版本的垂径定理已经在圆锥曲线中得到推广,见文献[1-3].

在文献[1-3]中,他们给出了椭圆、双曲线和抛物线的垂径定理:

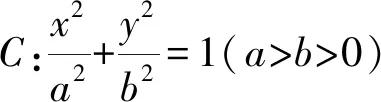
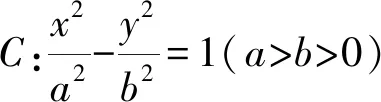
命题4 (抛物线的垂径定理) 已知抛物线y2=2px(p>0)与斜率存在且不为零的直线l相交于M,N两点,设MN中点为P(x0,y0),则有kMN·y0=p.

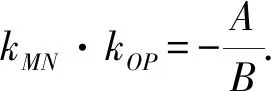
2 关于圆锥曲线垂径定理的一些问题

我们知道,命题5是关于有心二次曲线的垂径定理,它给出命题1～3的一种统一形式.实际上由解析几何知识可知,有心二次曲线不但包括圆、椭圆以及双曲线,还应该包括相交的双直线.因此,命题5并非完整地给出有心二次曲线的垂径定理.于是我们自然提出如下问题:

问题1相交的双直线的垂径定理是什么?

问题2 有心二次曲线与抛物线的统一垂径定理是什么?

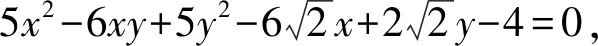
a1x2+b1xy+c1y2+d1x+e1y+f1=0,

①

其中,系数满足a1,b1,c1,d1,e1,f1∈R,且a12+b12+c12≠0.由于平面上的圆、椭圆、双曲线、双直线以及抛物线的标准或非标准方程都具有①的形式,因此上述问题可以总结为如下的问题3:

问题3设平面一般二次曲线方程为a1x2+b1xy+c1y2+d1x+e1y+f1=0,其中a1,b1,c1,d1,e1,f1∈R,且a12+b12+c12≠0,则相应的垂径定理如何?

3 平面一般二次曲线的垂径定理

本文我们主要给出问题3的答案,我们找到了如下的定理1.事实上,此结果可由文献[4]第203页的推论得到.但是,文献[4]对于该推论的证明涉及到一般二次曲线的渐近方向,该概念在高中数学未提及.为了使所涉及的方法不超出高中数学的范畴,在此我们利用高中数学常用的“点差法”给出该结果的一个证明.

定理1 设斜率存在的直线y=kx+m与平面一般二次曲线①相交于互异的M,N两点,且设线段MN中点为Q(x0,y0),则直线MN的斜率kMN满足关系式

(b1x0+2c1y0+e1)·kMN+2a1x0+d1+b1y0=0.

②

证明设M,N坐标分别为(x1,y1),(x2,y2).由于点M,N在平面二次曲线①上,故有

将③式减去④式,并且整理可得

⑤

由于点M,N在直线MN上,故有

⑥

将⑥代入⑤并且整理,可得

⑦

由于M,N互异,故x1≠x2.

因此,将⑦式两边除以x1-x2并且整理,可得

⑧

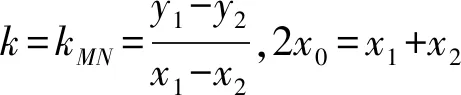
2x0(a1+b1kMN)+2c1y0kMN+d1+b1m+e1kMN

=0.

⑨

由于点Q(x0,y0)在直线MN上,

故y0=kMNx0+m.

解得m=y0-kMNx0,代入⑨并整理,得

(b1x0+2c1y0+e1)·kMN+2a1x0+d1+b1y0=0.

4 定理1对于命题1～5的推导

现在我们利用定理1的结果推出命题2.而命题1以及命题3～5的情形可类似给出,有兴趣的读者可自行检验,在此我们不再详细推导.

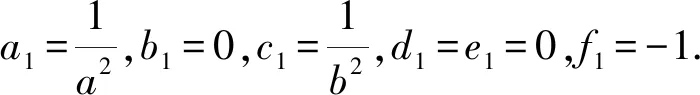
根据定理1,此时直线l的斜率kl满足方程

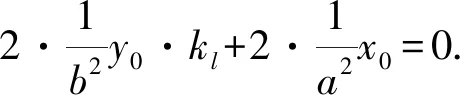
5 平面一般二次曲线垂径定理的应用

题目(2022年全国高中数学联赛江西省预赛试题第2题)若一直线l被另外两条直线l1:4x+y+6=0与l2:3x-5y-6=0所截得的线段的中点恰好是原点,则直线l的方程为____.

分析将直线l和直线l1的交点假设为(a,b),则根据条件可知点(-a,-b)在直线l2上.因此,有4a+b+6=0和-3a+5b-6=0.联立这两个方程可得a+6b=0,从而得出直线l方程为x+6y=0.考虑到相交的双直线是平面二次曲线①的一种,且题意涉及弦的中点,因此可以考虑平面一般二次曲线的垂径定理.

解析(双直线垂径定理法)将双直线l1:4x+y+6=0与l2:3x-5y-6=0写成平面二次曲线的形式,可得(4x+y+6)(3x-5y-6)=0,即

12x2-17xy-5y2-6x-36y-36=0,

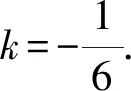
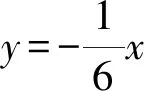
评注上述例题需要我们知道平面上的两条相交直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0可写成二次曲线的形式:

(A1x+B1y+C1)(A2x+B2y+C2)=0.

此外,与命题1～5的情形不同,上述例题的双直线的中心并不在原点处.这体现了定理1在处理一般二次曲线的垂径定理相关问题中所显示出来的优势.

6 结束语

总之,我们找到了椭圆、双曲线以及抛物线的垂径定理.其实,我们用高中数学常用的“点差法”证明了更加一般的结果,即定理1.该结果给出了圆、椭圆、双曲线、抛物线甚至双直线的垂径定理的一种统一形式.此外,定理1对于直线斜率等于零,以及对于中心不在原点处的圆锥曲线亦成立,这导致了定理1的使用范围更加广泛.