高中数学中的“同构”
乔建元
(陕西省旬阳第二中学,陕西 旬阳 725700)
在高中数学中,同构是一种重要的思想或方法,意指构造相同形式的结构,其不仅仅是一个表面上的等价关系,还是指两个数学结构之间具有相似的性质和结构特征.其虽未出现在教材中,但是却在某些方面起着举足轻重的作用.
1 同构在高中数学各方面的应用
1.1 集合方面
要找两个集合有某种关系时,先研究限定条件的相同点和不同点,通过相同点发现或者构造出相似的结构,这样只需研究不同点就可判断二者的关系.
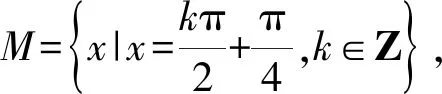
A.M=NB.M⊆NC.N⊆MD.M∩N=∅
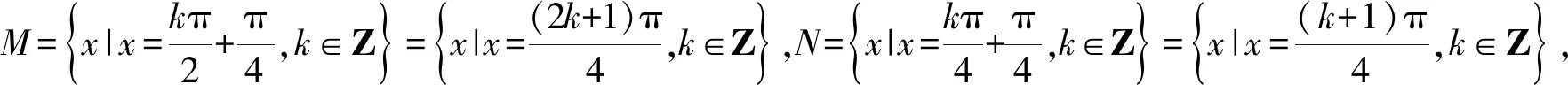
1.2 方程方面
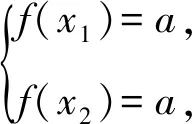
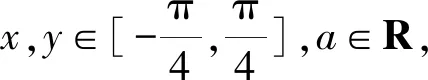
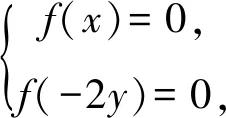
1.3 三角函数方面
对于同名三角函数,只需根据单调性得到两变量的大小关系;对于非同名三角函数,通过诱导公式和二倍角公式等将其化为同名三角函数即可.
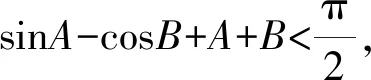
A.sinA
C.sinB 对于A,sinA>0,cosC<0,所以sinA>cosC,A选项错误; 同理,C选项正确; 在高考圆锥曲线问题中,常常会涉及三角形,而这些三角形中,往往会有几个点的运动是较为相似的,一般是在同一条直线上且在同一曲线上.因此,我们只需研究其中一个点和第三个点的关系,进而得出另一个点与第三个点的关系,亦即同构[1]. 例5已知抛物线C:x2=4y,⊙M:x2+(y+4)2=1,若点P在⊙M上,且PA,PB为C的两条切线,切点分别为A,B,求ΔPAB面积的最大值. 由韦达定理,得x1+x2=2x0,x1·x2=4y0. 函数的同构问题常见于指对混合函数的恒成立或零点问题中,重在观察和变形,所以技巧性较强.当然这类试题也可以用其他方法完成,那么在这里用同构思想,更多的是提升学生的直观想象、逻辑推理和数学运算素养[2]. (1)若f(x)≥0,求a的取值范围; (2)证明:若f(x)有两个零点x1,x2,则x1·x2<1. 则等价于a≤ex-lnx+(x-lnx). 令t=x-lnx,则a≤et+t. 易知h(x)的单调递增区间是(1,+∞),单调递减区间为(0,1),h(x)≥h(1)=1,即t≥1,易知et+t在t≥1时单调递增,所以a≤e+1(当t=1即x=1时取“=”.) 所以h′(x)>0,h(x)在x>1时单调递增, 所以h(x)>h(1)=0. 教育部考试命题专家表示:数学学科高考加强学科核心素养考查,强化数学思想方法的渗透,试卷深入考查关键能力,优化试题设计,发挥数学学科高考的选拔功能,助力提升学生的综合素质.数学核心素养的体现媒介之一就是同构思想,它几乎贯穿高中阶段的各个章节,在每年的高考题中都有体现.同构也是一种对称美,数学学科不仅深刻严谨,同时也给人以美的感受,所以广大考生应该重视同构思想,找到题中的关键点,化繁为简,在学习过程中注重积累总结,这样才能在考试中从容不迫,应对自如.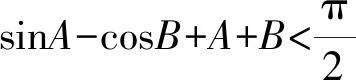
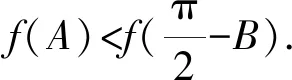
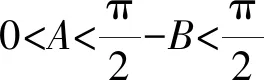
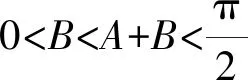
1.4 数列方面
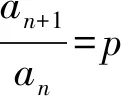
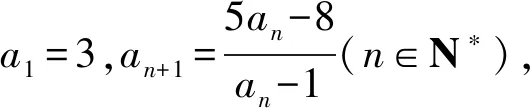
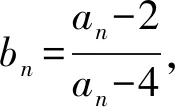
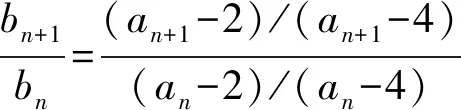
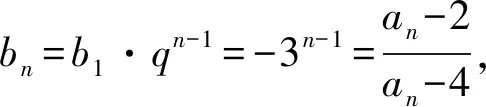
1.5 解析几何方面
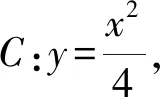
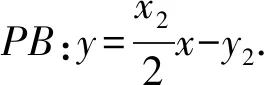
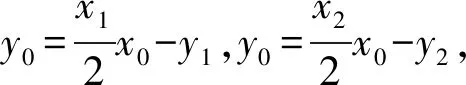
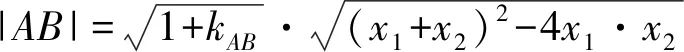
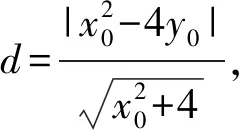
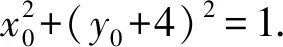
1.6 函数和导数方面
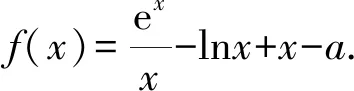
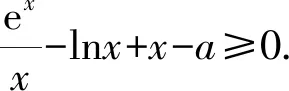
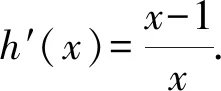
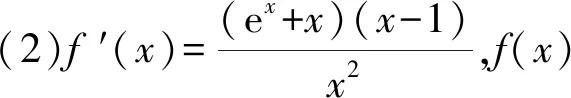
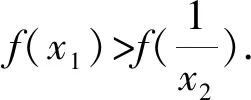
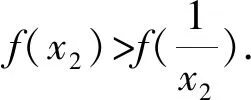
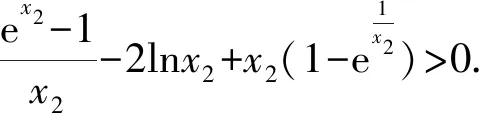
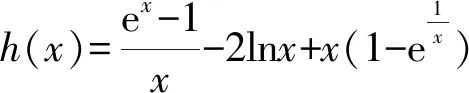
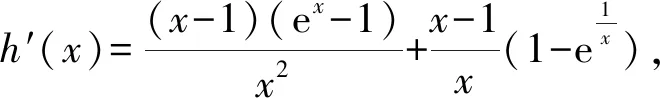
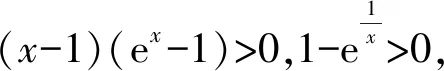
2 结束语

