对导数求参数取值范围问题解法的探究
——基于全国甲卷理科第21题的分析
孙 璪 王宇航
(1.遵义四中,贵州 遵义 563006;2.遵义市新浦中学,贵州 遵义 563103)
近年高考导数压轴题中求参数取值范围问题的题目出现频次较高,其中以特殊函数ex与lnx为背景的题目考查较多,但是2023年全国甲卷的导数压轴题以三角函数为背景,大有反套路、考能力的趋势.因此,如何找到求导数取值范围问题的通性通法显得尤为重要.
1 解法概述
分类讨论常常是解决该问题的一种通法.该方法一般是构造函数,然后通过求导、分类讨论、分析其单调性.
分离参数往往是解决该问题的一种重要方法,分离参数在解决恒成立问题时可以有两个角度:全分离和半分离.全分离是将含参表达式中的参数从表达式中完全分离出来,使所研究的函数由动态变为定态,进而可得到新函数的图象、性质(最值),将求参数的范围问题转化为求函数的最值或值域问题.半分离是将不等式变形为ax+b≥f(x)或ax+b≤f(x)的形式(其中a为参数,b为常数),然后画出图象,由图象的上下位置关系得到不等式,从而求得参数的取值范围.
必要性探路是解决该问题的一种妙法.必要性探路是指对某些与函数有关的恒成立问题,通过选取函数定义域内的某些特殊值,先得到一个必要条件,初步获得参数的范围,再在该范围内进行讨论,或去验证其充分性,进而得到参数的准确范围的方法.在验证其充分性的时候,往往需要结合“矛盾区间”进行说明.
泰勒展开是解决该问题的一种优法,许多高考题的命制如含有ex与lnx的题目,通常都是把其函数的泰勒展开式的几项进行直接变形,或取倒数、对数进行演绎变形,然后再结合添加参数设计而成.具有泰勒公式背景的高考数学试题大致可以分成两类问题,一类是根据不等式恒成立求解参数范围,一类是证明不等式恒成立[1].
2 解法探讨
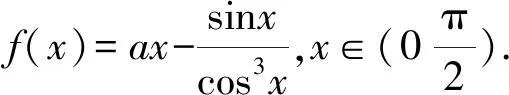
(1)当a=8时,讨论f(x)的单调性;
(2)若f(x) 本题的背景是三角函数,可通过构造函数用含参讨论法,讨论a在不同取值范围函数的单调性,从而知道所构造函数在定义域的最大值和零的大小关系. 又0 所以当a∈(-∞,3],f(x) 当t∈(t0,1),h(t)>0,即t0 综上,a的取值范围为(-∞,3]. 本题采用“半分离参数”法较为合适,可把条件f(x) 又3-2cos4x>0,故m′(x)>0. 必要性探路是先考虑函数的端点,再结合“矛盾区间”得出参数的取值范围的方法.“端点效应+矛盾区间”是一个完整的解题过程,其重点在于“矛盾”而非“端点”.缺少“矛盾区间”说明的解法,得到的仅仅是一个必要条件,显然过程是不完整的. 所以g′(x)≥0,即3-a≥0. 由泰勒展开式,我们可以得到: 由sin2x>f(x),得sin2x+tan3x+tanx-ax>0. 即sin2x+tan3x+tanx-ax>3x-ax. ②若a>3,同必要性探路解法. 处理导数中的参数取值范围问题有四个层次,正如本题的不同解法反映了不同的思维水平一样.学习导数的第一层次是“直接求导,分类讨论”,第二层次是“参变分离,数形结合”,第三层次是“端点效应,降低讨论”,第四层次是“泰勒展开,揭示本质”.如果学生解题总是只停留在第一层次就会自我设限,画地为牢,没有探究到导数的精髓.因此,我们倡导去探究通法通解,不被题目背景的表象所迷惑,去接近问题的本质.2.1 分类讨论,直面问题
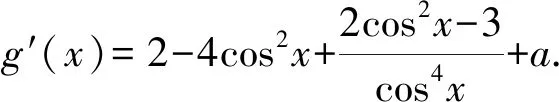
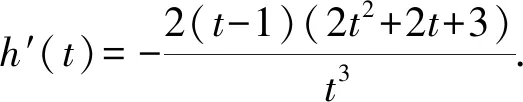


2.2 分离参数,数形结合

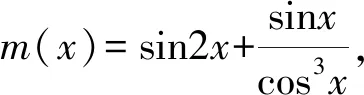
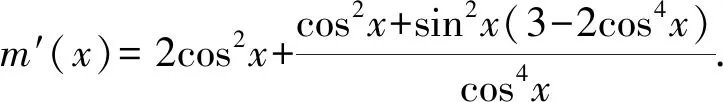
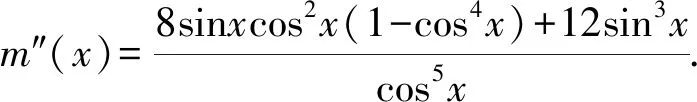

2.3 必要性探路,降低讨论
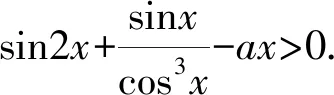
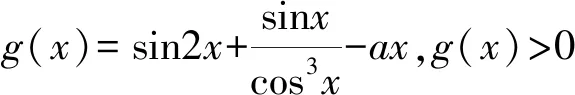

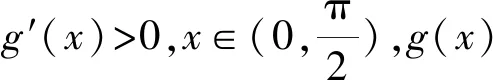

2.4 泰勒展开,揭示本质




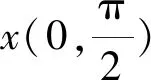

3 结束语

