运用交轨法求动点的轨迹方程

唐宜钟

(汉中市龙岗学校,陕西 汉中 723103)

轨迹问题是圆锥曲线的基本问题之一,其常用的解决方法有代数法和几何法两种.交轨法是代数方法中的一种,近些年在高考、各地模拟题中都有所涉及.

1 交轨法的定义

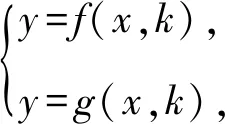
2 交轨法的选参和消参

2.1 直接解方程消参

例1已知正方形的四个顶点分别为O(0,0),A(1,0),B(1,1),C(0,1),点D,E分别在线段OC,AB上运动,且OD=BE,设AD与OE交于点G,求点G的轨迹方程.

解析设D(0,m)(0≤m≤1),则E(1,1-m).

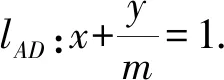
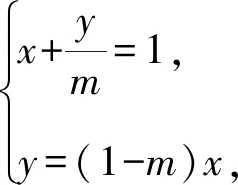
消去m可得y=(1-x)x(0≤x≤1).

评析本题属于交轨法的“入门问题”.选取点D的纵坐标为参数,进而能得到点E的坐标,所有直线都能够表示出来.对于所列方程组,可以直接把m当成已知量,解出x和y.再利用m=x,代入y=(1-m)m即可得到轨迹方程.最后,需要根据初始参数m的取值范围及运算过程中各个条件和运算式的限制,界定轨迹的范围,去掉方程中的特殊点.

2.2 相乘消参

解析设P(x,y)及M(x1,y1),N(x1,-y1),又A1(-a,0),A2(a,0),

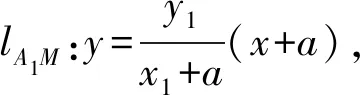
①

②

③

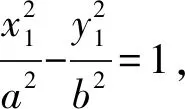
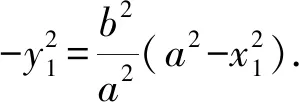
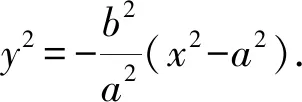
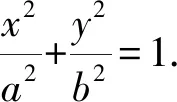
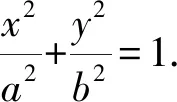
当a=b时,点P的轨迹是以原点为圆心,a为半径的圆;当a≠b时,点P的轨迹是椭圆.

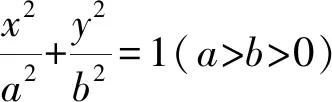
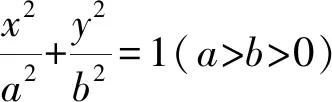
则N(acosθ,-bsinθ).

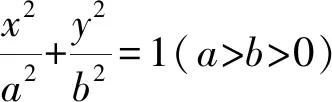
两式相乘,得

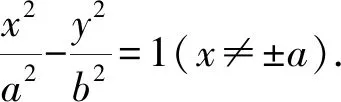
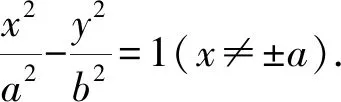
评析例2和例3属于交轨法的经典范例.其中,例2选取了点M(x1,y1)为参数,例3选取了椭圆的辐角θ为参数,再利用两直线方程相乘消去了参数.其本质是利用了有心曲线的第三定义:A,B是有心曲线上关于原点对称的两点,P(x,y)为有心曲线上异于A,B的一点,则kPA·kPB=e2-1[1].例2和例3从代数角度“佐证”了第三定义.事实上,只要两条直线斜率相乘呈现一定的代数特征(如为定值),就可以尝试使用乘法消元.当然,在使用过程中,依旧要注意参数的取值范围,以便在最终结果中去掉特殊点.

2.3 零因式消参

例4 已知抛物线y2=4x,过顶点的两弦OA,OB互相垂直,求以OA,OB为直径的两圆的另一交点的轨迹方程.

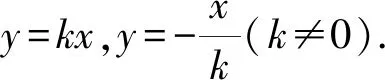
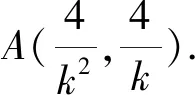
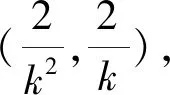
即k2(x2+y2)-4x-4ky=0.

④

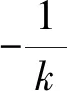
⑤

④+⑤,得(1+k2)(x2+y2-4x)=0.

因为1+k2≠0,所以x2+y2-4x=0.

所以以OA,OB为直径的两圆的另一交点的轨迹方程为x2+y2-4x=0(x≠0).

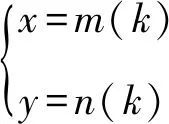
2.4 同构消参

所谓同构是指若方程f(a)=0,f(b)=0呈现出共同特征,则a,b可视为方程f(x)=0的两个根.其常应用于切线和切点弦问题,因为这类问题初始时通常会用多个参数,通过同构可以达到“多参化一”的效果.

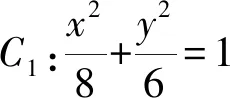
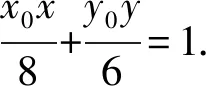
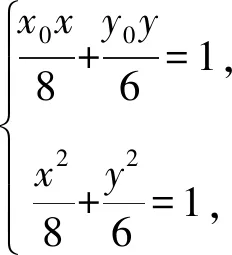
故椭圆C1在点P处的切线方程为

设点M(x1,y1),再证圆C2在点M处的切线方程为x1x+y1y=24.

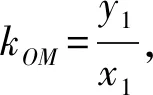
故圆C2在点M处的切线方程为

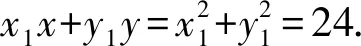
当直线OM的斜率不存在且为零时,在点M处的切线满足上式.

设点N(x2,y2),则圆C2在点N处的切线方程为x2x+y2y=24.

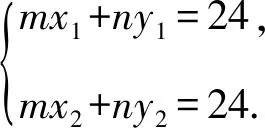
故点M,N的坐标满足方程mx+ny=24.

故直线MN的方程为mx+ny=24.

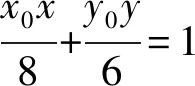
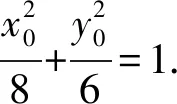
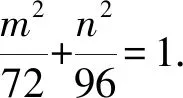
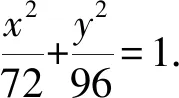
2.5 动点转移法消参

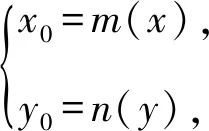
例6 如图1,已知抛物线C:y=x2,动点P在直线l:x-y-2=0上运动,过点P作抛物线C的两条切线PA,PB,且与抛物线C分别相切于A,B两点.求△APB的重心G的轨迹方程.

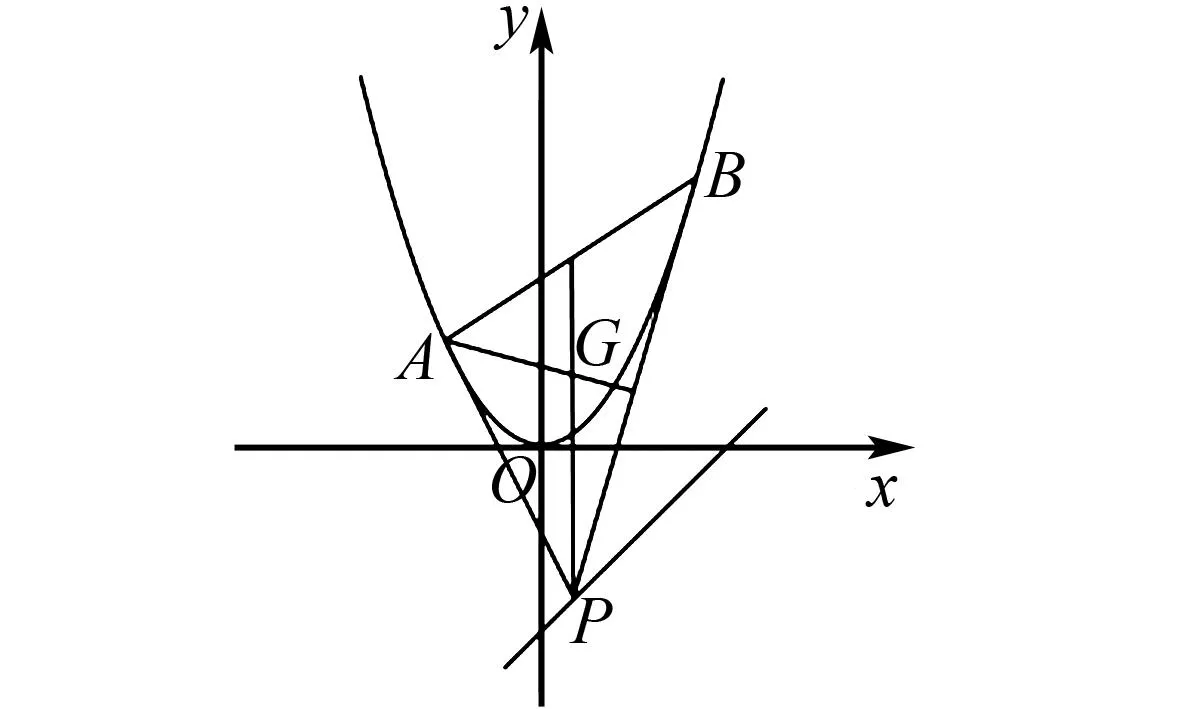
图1 例6题图

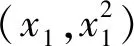
求导可得kAP=2x1.

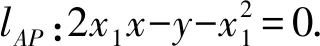
由于点P既在AP上又在BP上,

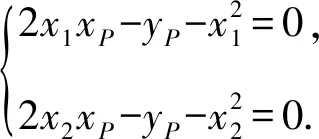
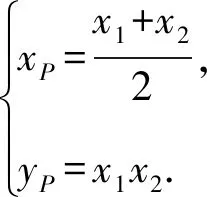
所以△APB的重心G的坐标为

⑥

⑦

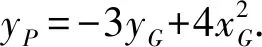
由点P在直线l:x-y-2=0上运动

所以xP-yP-2=0.

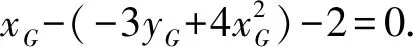
从而得到重心G的轨迹方程为

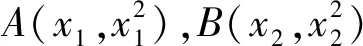
2.6 利用曲线性质消参

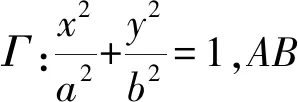
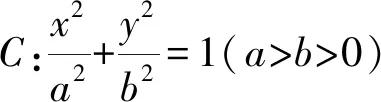
(1)求C的方程;

(2)如图2,点P,Q分别在C和直线x=4上,OQ∥AP,M为AP的中点,求证:直线OM与直线QF的交点在某定曲线上.

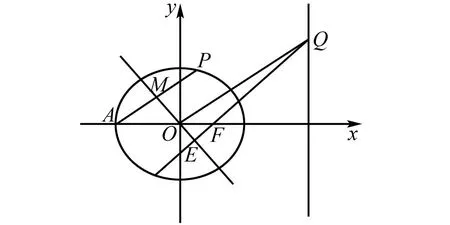
图2 例7题图

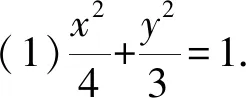
(2)显然,kAP存在且不为0,设kAP=kOQ=k,则lOQ:y=kx,故yQ=4k,即Q(4,4k).

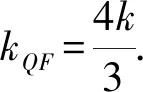
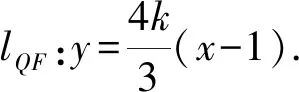
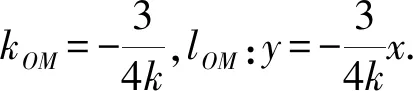
两直线方程相乘,得y2=-x(x-1).

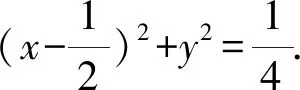
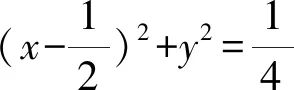
2.7 利用曲线的几何意义消参

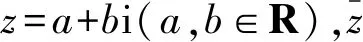
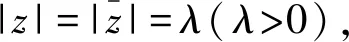
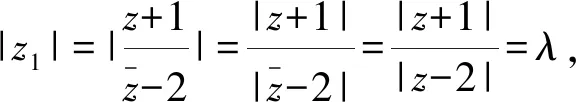
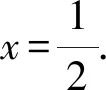
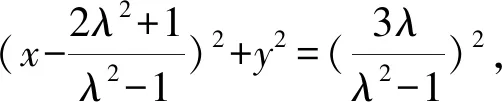
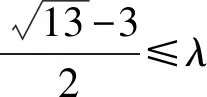
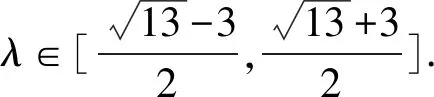
评析本题背景虽为复数,但从复数模长的几何意义上看,题目的实质是满足条件的点的轨迹,即两圆有公共点,直接利用圆的相关知识解决即可.

3 结束语

在选取参数时,除了常见的动点坐标、斜率、角度外,线段比值、截距等也都可以在相应的题目中使用[2].在具体消参过程中,要代数技巧、曲线性质和几何意义相结合,力求做到消参路径的顺畅、计算的简单、几何意义的明确.在得出轨迹方程后,需要从题目本身及消参过程中参数的条件限制去掉特殊点.从方程轨迹的几何意义再去思考题目,明晰轨迹的生成过程,从“数”和“形”两方面,进一步加深对题目的理解.