一道解析几何试题的深入探究

林国红

(广东省佛山市乐从中学,广东 佛山 528315)

圆锥曲线中的定值定点问题是高考或各类模考的热点问题之一,这类问题能够在考查圆锥曲线基础知识的同时,又能很好地考查学生的运算求解、推理论证等数学能力,以及对分类讨论、转化与化归等数学思想的理解水平.下面以一道试题为例,深入探讨一类与斜率和(积)有关的定值定点问题.

1 试题的呈现与解答

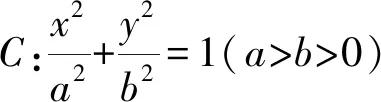
(1)求椭圆C的方程;

(2)若P为椭圆C的左顶点,A,B为椭圆C上的两点,设直线PA,PB的斜率分别为kPA,kPB,且满足kPA+kPB+kPAkPB=1.求证:直线AB过定点.

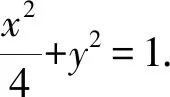
(2)由(1)可得P(-2,0),设直线AB的方程为m(x+2)+ny=1.

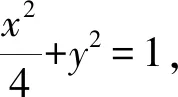
整理,得4y2+(x+2)2-4(x+2)=0.

联立直线AB,齐次化,得

4y2+(x+2)2-4(x+2)[m(x+2)+ny]=0.

化简,得

4y2-4n(x+2)y+(1-4m)(x+2)2=0.

两边同除(x+2)2,得

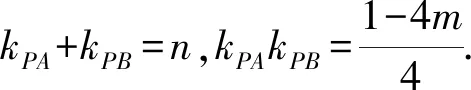
代入kPA+kPB+kPAkPB=1,得

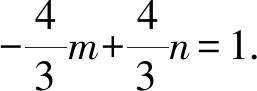
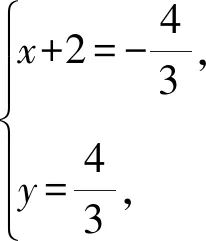
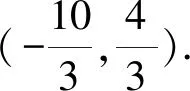
评注齐次化法在解决两直线斜率之和(积)相关的定值定点问题中运算量较少,常能达到化繁为简的效果[1].

2 问题的提出

结合试题,思考:

问题2 在问题(2)中,如果把椭圆C一般化,则直线AB是否过定点?

问题3 在问题(2)中,如果把椭圆C改为双曲线或抛物线,则直线AB是否过定点?

问题4 在问题(2)中,如果直线AB过定点,那么直线PA,PB的斜率和与斜率积有什么关系?

3 结论推广

通过探究,可得如下结论:

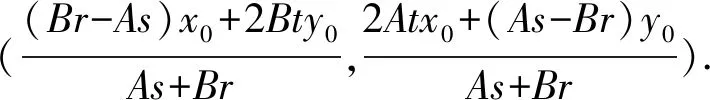
证明设直线MN的方程为

m(x-x0)+n(y-y0)=1,

由Ax2+By2=1,变形,得

A(x-x0+x0)2+B(y-y0+y0)2=1.

整理,得A(x-x0)2+B(y-y0)2+2Ax0(x-x0)+2By0(y-y0)=0.

联立直线MN,齐次化,得

A(x-x0)2+B(y-y0)2+[2Ax0(x-x0)+2By0(y-y0)]×[m(x-x0)+n(y-y0)]=0.

化简,得

(B+2Bny0)(y-y0)2+2(Anx0+Bmy0)(x-x0)(y-y0)+(A+2Amx0)(x-x0)2=0.

两边同除(x-x0)2,得

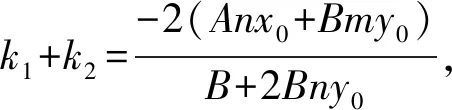
(1)当sk1k2+t(k1+k2)+r=0时,可得

整理,得

m(2Bty0-2Asx0)+n(2Atx0-2Bry0)=As+Br.

(ⅰ)若As+Br≠0,则

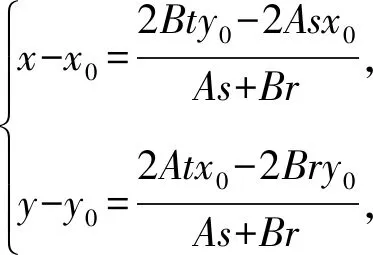
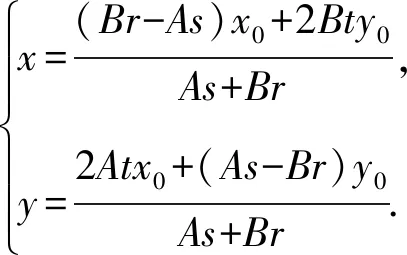
所以直线MN过定点

(ⅱ) 当As+Br=0,则

m(2Bty0-2Asx0)+n(2Atx0-2Bry0)=0.

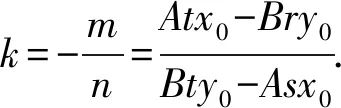
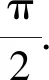
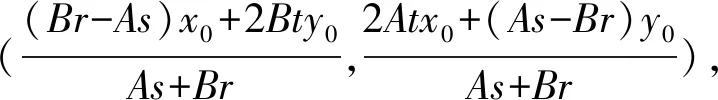
所以sk1k2+t(k1+k2)+r=0.

综合(1)(2),结论1得证.

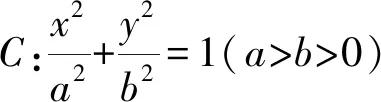
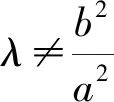
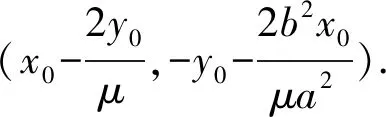
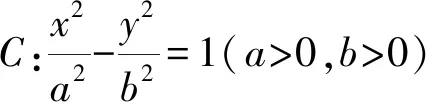
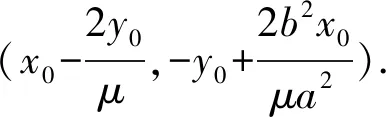
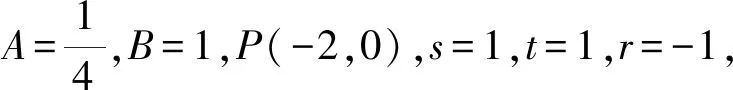
4 类比性质

双曲线、抛物线与椭圆都是圆锥曲线,很多时侯三者之间有可类比的性质,这体现了圆锥曲线性质的内在统一的和谐美.那么抛物线是不是也有类似于结论1的性质呢?经探究,得到如下结论:

证明设直线MN的方程为

m(x-x0)+n(y-y0)=1.

由y2=2px,变形,得

(y-y0+y0)2=2p(x-x0+x0).

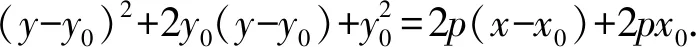
即(y-y0)2+2y0(y-y0)-2p(x-x0)=0.

联立直线MN,齐次化,得

(y-y0)2+2y0(y-y0)·[m(x-x0)+n(y-y0)]-2p(x-x0)·[m(x-x0)+n(y-y0)]=0.

化简,得(1+2ny0)(y-y0)2+(2my0-2pn)(x-x0)(y-y0)-2pm(x-x0)2=0.

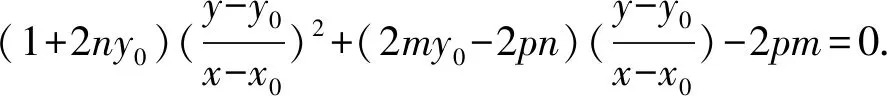
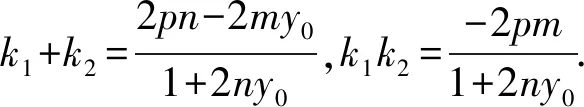
(1)当sk1k2+t(k1+k2)+r=0时,得

整理,得(2ps+2ty0)m+(-2pt-2ry0)n=r.

(ⅰ)若r≠0,则

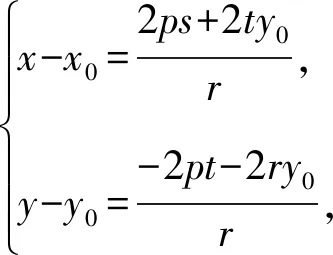
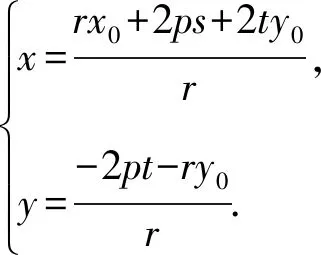
(ⅱ)当r=0,由(2ps+2ty0)m+(-2pt-2ry0)n=r,得m(2ps+2ty0)+n(-2pt)=0.

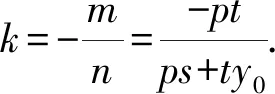
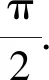
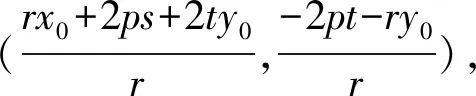
所以sk1k2+t(k1+k2)+r=0.

综合(1)(2),结论2得证.

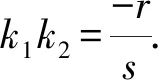
推论3 过抛物线C:y2=2px(p>0)上的定点P(x0,y0)作斜率为k1,k2的两条直线分别与抛物线C交于M,N两点.

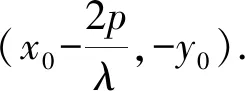
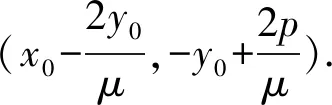
5 结束语

高中数学新课程理念之一是倡导积极主动、勇于探索的学习方式.教师可根据学生实际,通过对题目的拓展、引申、变式探究,让学生体验数学的发现和创造历程,引导他们勇于发现问题、提出问题、解决问题,进而让学生在分析、类比、猜想、证明过程中养成对数学结论背后逻辑关系的分析与思考习惯,促进学生的发展,提高学生的综合能力,从而提升学生的数学核心素养.