一道高考圆锥曲线试题多解的深度探究与启示
安中顺 余 泉
(贵州省都匀一中,贵州 都匀 558000;2.黔南民族师范学院,贵州 都匀 558000)
圆锥曲线中直线过定点的问题是近些年高考常考的一种题型,基本都是以压轴题出现,人们常用“高考常青树”来形容[1].对于这一题型学生很难拿到较高的分数,本文以2020年高考数学全国Ⅰ卷理科第20题为例,详细讨论了本题直线过定点问题多种解法中的6种特别解法.
1 题目呈现与解答
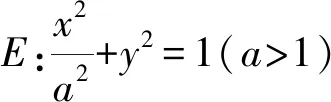
(1)求E的方程;
(2)证明:直线CD过定点.
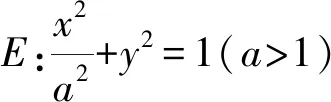
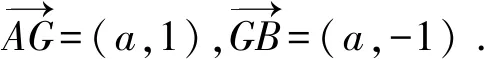
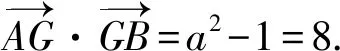
所以a2=9.

本题第(2)问中,高考参考答案解法破解难度大,需依托数学模型,强调对数学思想方法的考查,要求学生具有较高计算能力和细致、全面的思维品质.笔者从近些年的直线过定点考题中分析问题并从深度探究与教学的不同角度给出建议,用6种不同解法加以阐述.

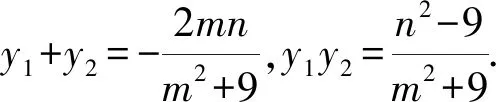


提取公因式,该等式一定可化为
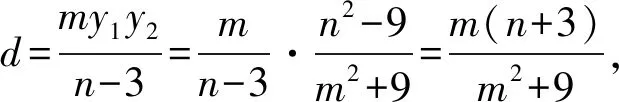

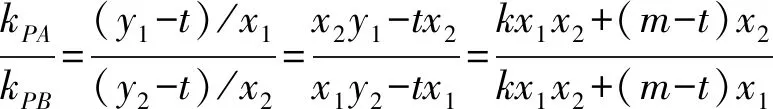
解法2设点P(6,t),直线CD的方程为x=my+n,由题意可知-3 由于直线PA的方程为tx-9y+3t=0, 直线PB的方程为tx-3y-3t=0, 过A,B,C,D四点的曲线系方程可设为 点评经过两曲线f1(x,y)=0和f2(x,y)=0交点的一系列曲线的方程为f1(x,y)+λf2(x,y)=0.如果f1(x,y)=0和f2(x,y)=0齐次,则f1(x,y)+λf2(x,y)=0表示过两已知曲线交点的一系列同构的曲线,如果f1(x,y)=0和f2(x,y)=0都是圆,则f1(x,y)+λf2(x,y)=0也是圆.综合起来,可以理解为f1(x,y)=0和f2(x,y)=0相交形成了曲线系f1(x,y)+λf2(x,y)=0. 解法3(截距式)设C(x1,y1),D(x2,y2),P(6,t),易知3kPA=3kAC=kPB=kBD. 即3x2y1-y2x1=3y2+9y1. ① x2y1-3x1y2=-3y1-9y2. ② 由①+②,得4x2y1-4x1y2=6y1-6y2. 解法4 设点P(6,t),点C(3cosα,sinα),D(3cosβ,sinβ),则 设CD过定点为M(m,0), 由kMD=kCM,得 点评对于圆锥曲线中的双斜率问题, 常规方法是联立方程结合韦达定理求解;也可以通过齐次化处理,利用齐次式解决更加方便快捷,可简化运算,降低运算难度. 齐次化方法一般适用于两直线斜率之和(或积)为常数的题型,可以解决与斜率之和(或积)有关的定点、定值或轨迹等问题.使用齐次化方法时,需要注意两个关键步骤: 步骤1:先平移坐标系, 将定点P(x0,y0)平移至原点O(0,0),平移公式x′=x-x0,y′=y-y0,其中(x′,y′)为新坐标,(x,y)为同一点旧坐标. 通过对圆锥曲线问题的深度探究,学生从“会通性通法”到“能变式解法”,再到“会创新解法”,有利于培养学生发现问题和解决问题的能力,在探究过程中让学生的综合素质得到发展.总之,对学生解压轴题能力提升的探究不是一朝一夕就能完成的,也不是仅通过几个题目的多种解法就可以强化的,它需要学生领会圆锥曲线中直线过定点或定斜率问题呈现背景的多样性.因此,学生要注重以必备知识和方法为起点,借助模型和师生合作探究挖掘更多的探究点,从圆锥曲线性质多方面进行渗透,促进学生将直线过定点或定斜率的知识掌握得更牢固.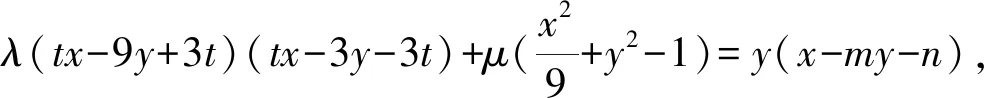

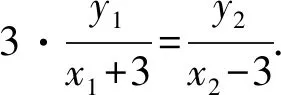
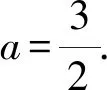

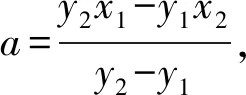


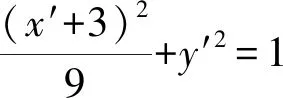

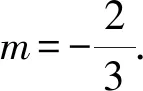
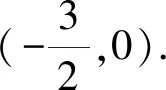


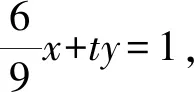
2 结束语

