立足双曲定线 长路解法漫漫——一道高考题的赏析

张 悦

(江苏省扬州市扬州大学,江苏 扬州 225009)

数学运算素养是新课程标准提出的六大核心素养之一,而圆锥曲线解题教学是培养学生数学运算素养的良好载体.它本质是一种思维模式,这种思维模式的过程包括:理解运算对象→掌握运算法则→探求运算思路→选择运算方法→设计运算程序→求得运算结果[1].在解决圆锥曲线定线问题的过程中,最常见的解题思路是联立直线和曲线后通过设出方程求解,本文在此基础上,又从几何和代数角度给出多种解题策略供读者参考.

1 真题呈现

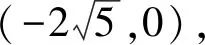
(1)求C的方程;

(2)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于M,N两点,点M在第二象限,直线MA1与NA2交于点P.证明:点P在定直线上.

2 解法赏析

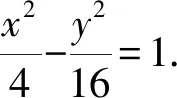
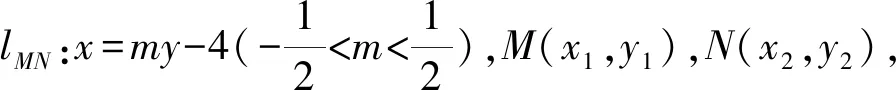
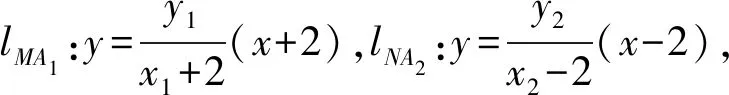
所以点P在定直线x=-1上,

解法2 (设而不求)联立直线与曲线方程

(4m2-1)y2-32my+48=0.

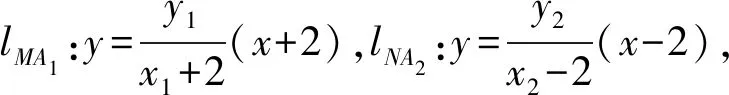
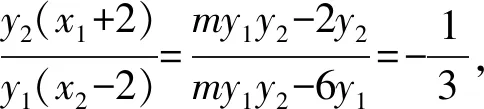
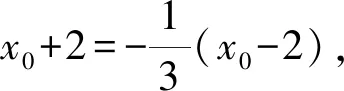
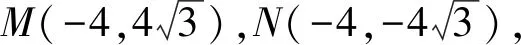
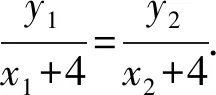
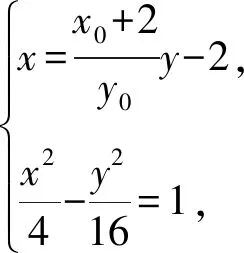
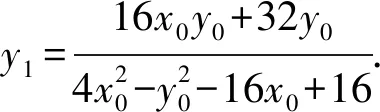
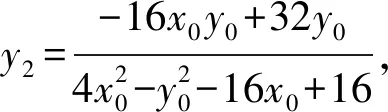
又因为点P不在双曲线上,所以x0=-1,

解法5 (“第三定义”)由M(x1,y1),N(x2,y2)在双曲线上可得到

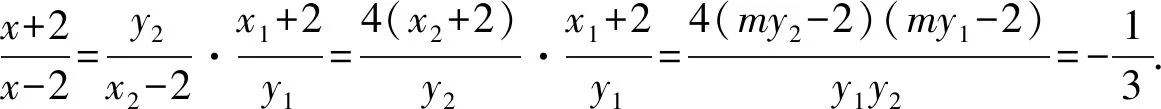
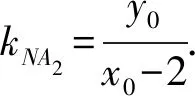
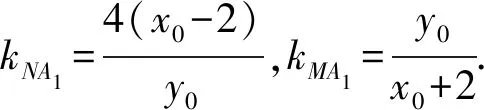
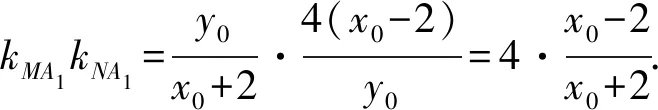
将双曲线C向右平移2个单位,得

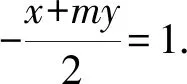
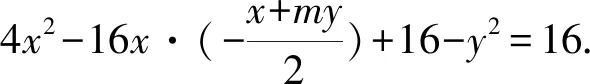
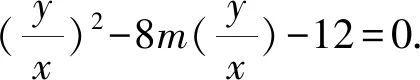
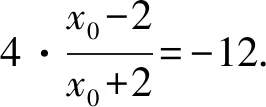
解法7 (整体换元)联立直线和双曲线有

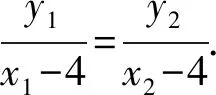
化简,得x2y1-x1y2=4(y2-y1),

①

x2y1+x1y2=(my2-4)y1+(my1-4)y2

=2my1y2-4y1-4y2.

②

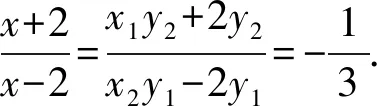
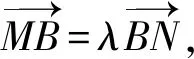
x1+λx2=-4-4λ,y1+λy2=0.

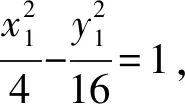
③

④

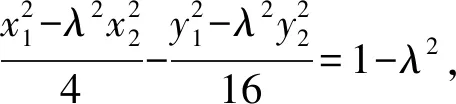
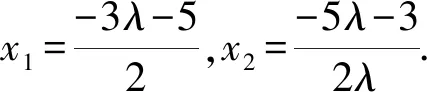
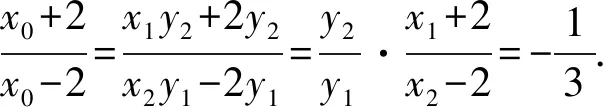
所以x=-1.

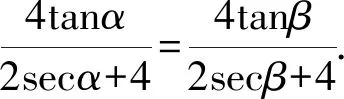
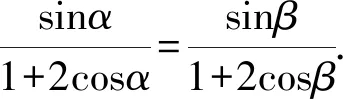
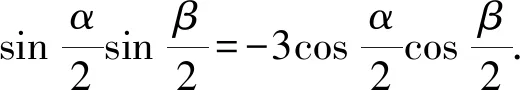
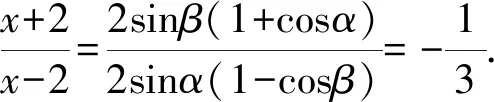
3 延伸拓展

圆锥曲线的极点和极线定义:如图1(以椭圆为例),点P是圆锥曲线外的一点,过点P引出两条割线,与圆锥曲线依次相交于E,F,G,H四点,连接EH,FG,两线交点设为点N;再连接EG和FH,两线交点设为点M,其中直线MN称为点P对应的极线;如果点P位于圆锥曲线上,则过点P的切线就为该点的极线.

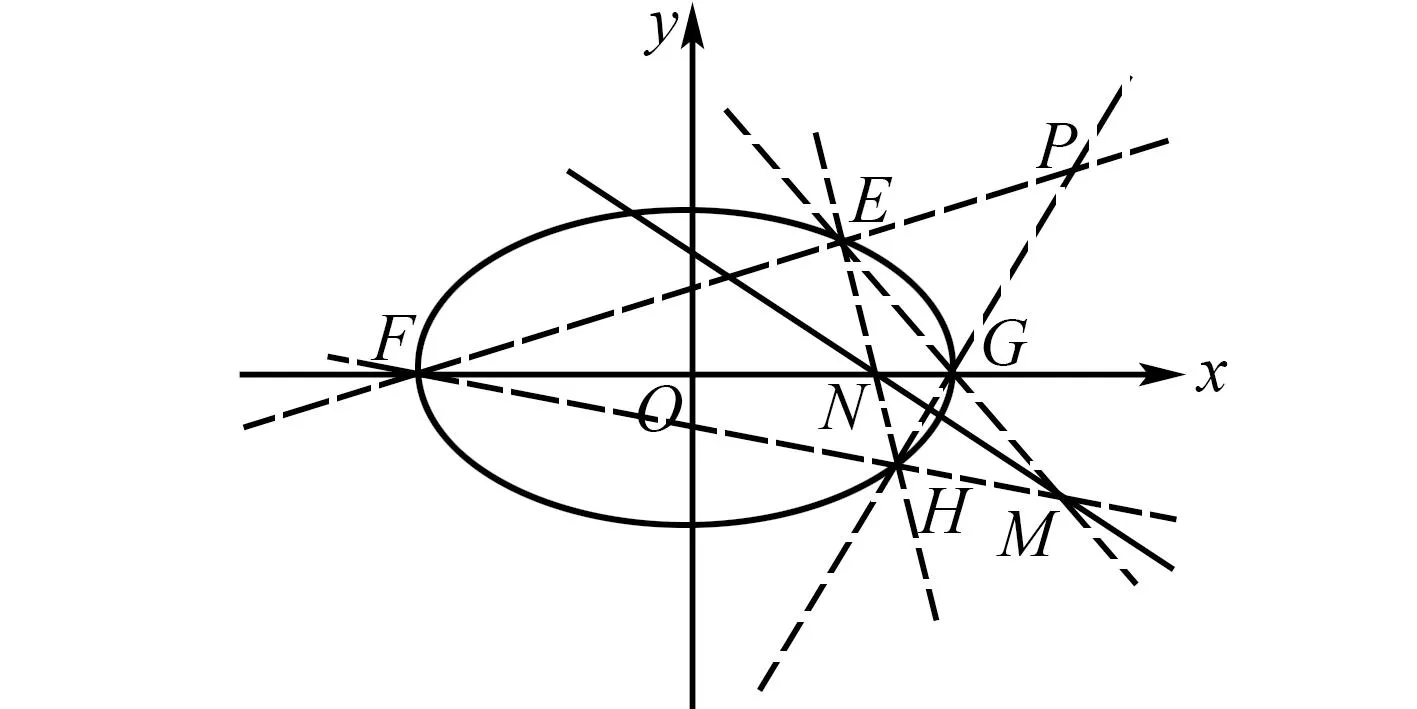
图1 椭圆示意图

笔者深入研究发现,定点(-4,0)和定直线x=-1类似于圆锥曲线中的极点和极线,那么基于定点定线和极点极线知识体系的统一性,将双曲线的探究背景置换成椭圆和抛物线,得到相应结论.

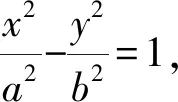
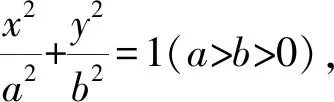
结论3抛物线(焦点在x轴):已知抛物线C的方程为y2=2px(p>0),过定点(s,0)(s≠0)的直线与C交于M,N两点,过M,N分别作抛物线的切线,两条切线相交于点P,则点P在定直线x=-s上.

4 结束语

大道至简,也如同高考定直线试题有极点极线知识背景一般,将试题抽丝剥茧后抓住核心定点对应定直线,在解析几何中可以直接利用这些结论较为快速地解题.笔者希望通过本题的多视角求解和多方面延伸,促使学生对圆锥曲线进行整体认知建构,提升数学运算核心素养.