一道2023年高考题的多解和思考
刘社新
(盐城市滨海县明达中学,江苏 盐城 224599)
以平面向量为背景的题目作为高考压轴题虽然不多,但是每次出现都很新颖,感觉似曾相识,又相去甚远,入手难,推进更难.这是因为平面向量具有代数和几何双重性,往往使题目具有迷惑性、开放性[1].
1 试题呈现
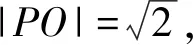
2 总体认识
本题作为选择压轴题自有其独到之处,具体表现为:首先,背景知识丰富,有圆与直线相切的位置关系,圆与直线相交的位置关系,弦中点,数量积运算和最值;其次,表象上虽属于常规题,却很有新意,融合度高,思路开阔,高度体现了高考的改革风向:注重数学思想、方法的考查.
3 解法探究
思路1 按照数量积的定义计算,从题设中寻找两个向量的模,引入角来联系向量的模与向量夹角,构造三角函数求最值[2].
解法1如图1,连接AO,DO,因为直线PA与圆O相切于点A,所以AO⊥PA.
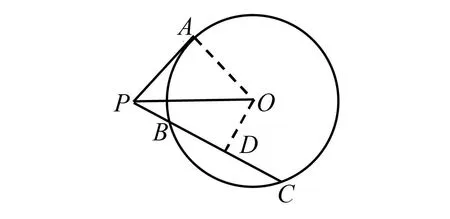
图1 解法1示意图
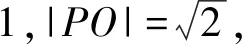
所以△PAO为等腰直角三角形.
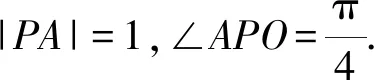
设∠OPD=β,当直线PA,PD在PO同侧时,记为β负角;当直线PA,PD在PO异侧时,记为β正角.
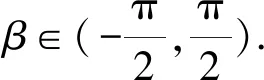
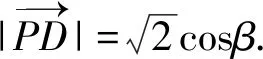
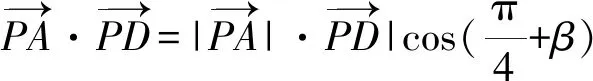
=cos2β-sinβcosβ
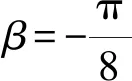

故选A.
评析本解法容易想到,但是角β的范围容易失误,误判为锐角,从而取错最值.对于正负角的考查实属精辟,也是创新,体现了学以致用的教学精髓.以前不曾在正负角这个知识上做文章,或者说,以前应用较为浅显.
思路2 用特值法固定点A和点P,为引进直线参数方程构造条件,将向量问题转化为三角问题.
解法2 不失一般性,如图2,依据题意,可令A(0,1),P(1,1).
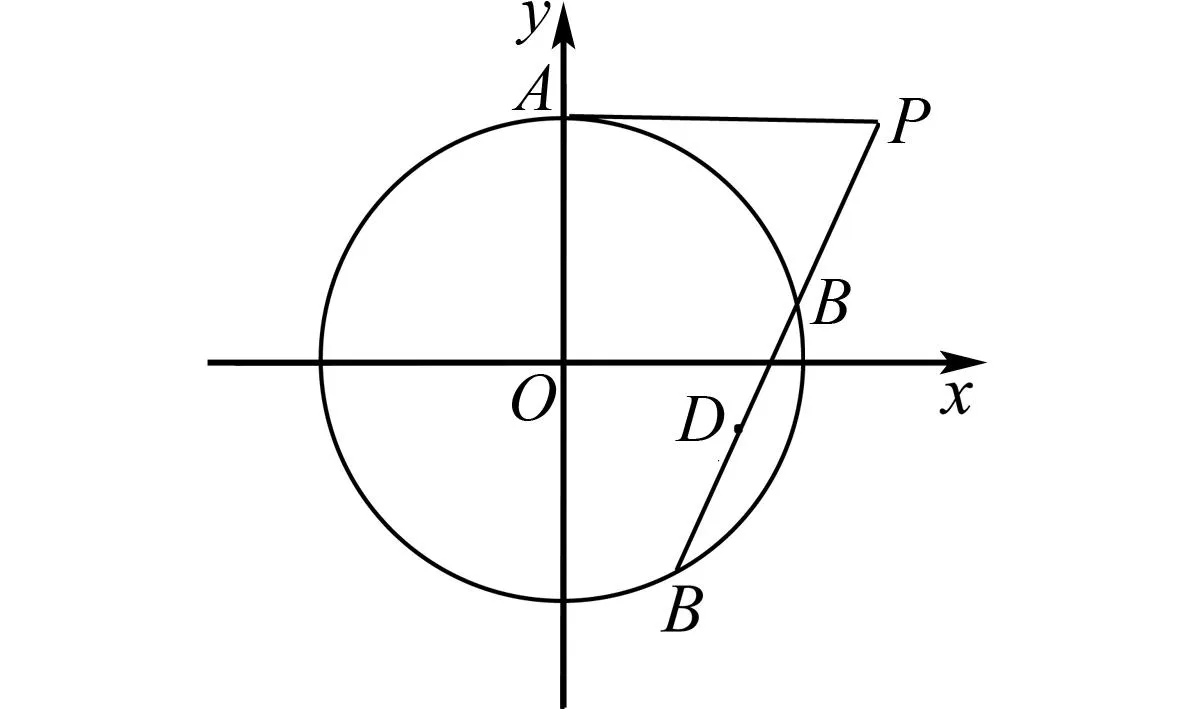
图2 解法2示意图
易得圆O:x2+y2=1,
①
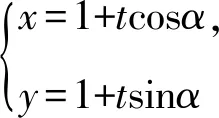
②
将②代入①整理,得
t2+2(sinα+cosα)t+1=0.
所以t1+t2=-2(sinα+cosα).
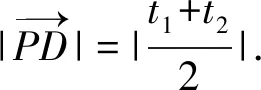
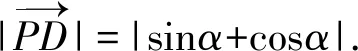
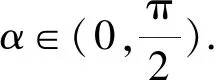
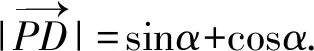
易知AP∥x轴.
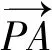
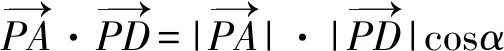
=1×(sinα+cosα)×cosα
=cos2α+sinαcosα
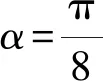

故选A.
评析本解法处理模长和夹角都显得简捷,当然概念性更强.将直线BC的倾斜角直接转化为向量的夹角,比解法1简单,也使后续运算方便许多.参数方程的引入是本解法的关键.
思路3 抓住直线与圆相切,以及圆的中点弦,利用垂径定理,易知A,P,D,O四点共圆,利用平面向量的坐标运算解题.
解法3 如图3,以线段PO所在直线为x轴,线段PO的中垂线为y轴,新的原点记为E,建立平面直角坐标系.
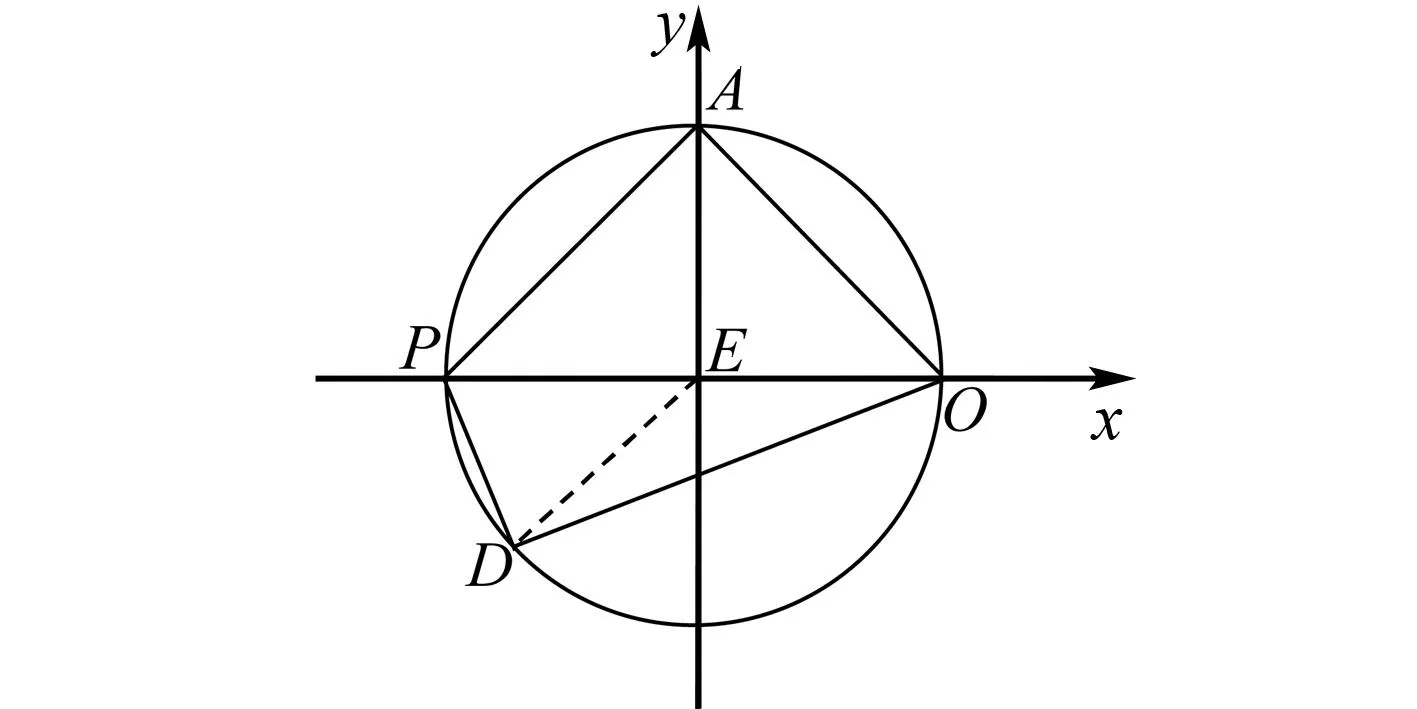
图3 解法3示意图
连接AO,因为直线PA与圆O相切于点A,
所以AO⊥PA.
因为D为BC中点,
易得A,P,D,O四点共圆,记为圆E.
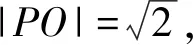
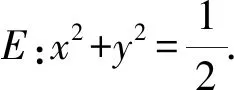
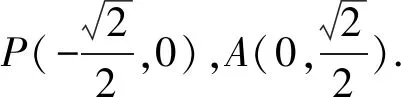
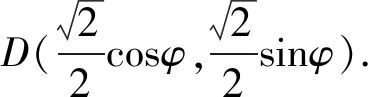
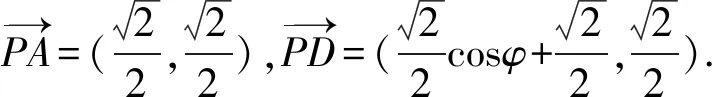
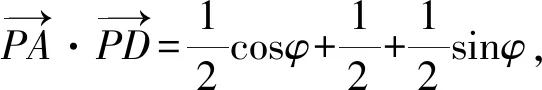
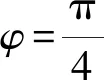
故选A.
评析这种方法变换了坐标系,被研究元素的坐标具体化、简单化,从而使相关向量坐标可视化,于是数量积就水到渠成.将抽象复杂问题简单化,需要较高的逻辑推理能力,从而简化运算.
思路4 本题中,点P的位置不影响问题的本质,因此可以特殊化,从而可以确定点A,于是可以把问题归结为动直线BC与圆O的相交关系下的函数问题.
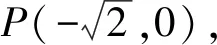
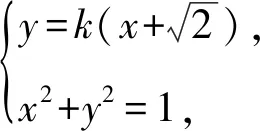
因为直线BC与圆O相交,
所以Δ=8k4-4(1+k2)(2k2-1)>0,
解得-1 故选A. 评析本解法是圆锥曲线的通解通法,借助导数求出最值,平时教学加强训练,既对小题有帮助,又对解析几何的压轴大题有支撑作用. 思路5 处理复杂函数是学生的难点,解法4中处理函数最值也可以从均值不等式入手,构造均值不等式是关键. 解法5 结合解法4, 因为-1 评析这类函数最值是常见模型,处理过程中要注意三点:一是定义域的限制,二是定值(常数)的构造,三是当均值不等式失效的情况下,及时利用对勾函数补救.这个问题可以衍生出其他类型的最值问题. 以上每种类型的处理办法不尽相同,有兴趣的同仁可以仔细研究. 参考答案:B. 突破高考压轴题要在日常教学中下功夫,尤其不能有畏难思想,比如遇到“难题”“新题”就因为害怕而放弃,因为下次可能不再遇见就侥幸过关,因为耗时较多就搁下,等等.事实上,只有加强耐挫力的培养,学生才能提高学习自信心.通过一定次数的磨砺,所谓的难题也就在感觉上变得容易.否则,学生的应试能力节节败退,高端题害怕,中档题也担心. 突破高考压轴题要在基本功上下功夫,不能搞套路化训练.因为基本功扎实了,思路就开放了,逻辑就连贯了,运算就准确了,速度也自然提升了.反之,被灌输一些套路的学生遇到新情景、新问题就只能束手就擒,无计可施,在考场上情绪激动,影响整场考试心理,这就是常说的“平时学得很好,高考没发挥出来”.本题中,求函数的最值需要学生良好的基础,无论是三角出口,还是分式函数出口都是日常教学的重点.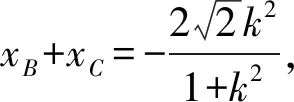
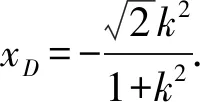
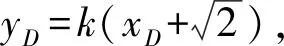

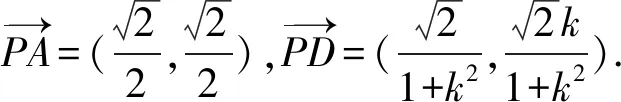
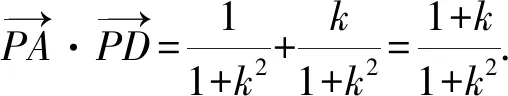

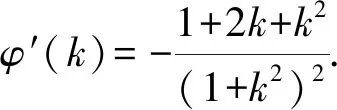
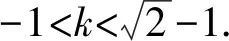
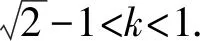
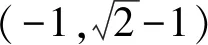
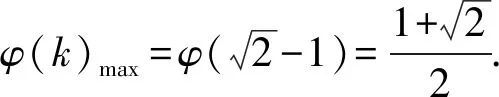
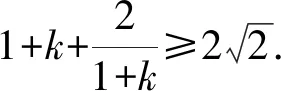
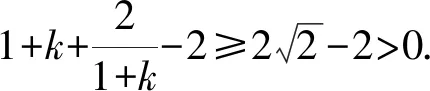
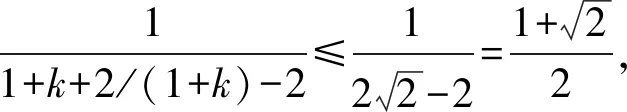
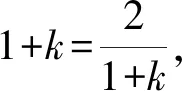
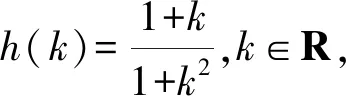
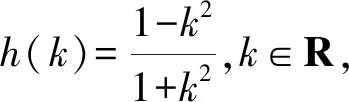
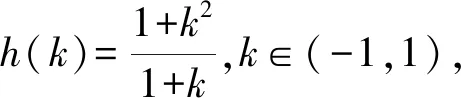
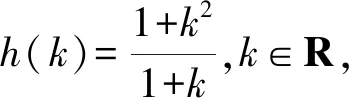
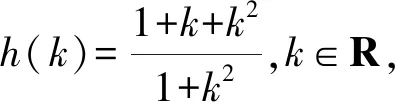
4 高考链接

5 结束语

