2023年贵阳市二模数学第12题的多解、溯源

李 勇

(贵阳市息烽县第一中学,贵州 贵阳 551100)

该试题作为一道压轴题,起点比较高.绝大多数的考生由于自身知识储备的问题,只能按套路解题,这将导致由于产生大量的运算而无法进行下去,因此绝大多数的考生这道题得不到分.其实这道题的落点是很低的,就是考查抛物线的性质,准确一点讲就是考查抛物线中过焦点的阿基米德三角形的性质,对于那些掌握了抛物线有关性质的学生来说这道题就是一道送分题,是非常简单的.

1 试题呈现

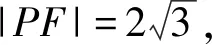
A.5 B.6 C.7 D.8

2 背景探究

此题明面上是考查抛物线的切线问题,实则考查的是过焦点的阿基米德三角形问题[1].该三角形比一般的阿基米德三角形有着更多的性质,因此常被出题人青睐.下面列举此三角形的一些常考性质.

已知抛物线C:y2=2px(p>0)的焦点为F,过焦点F的直线交抛物线C于A,B两点,以A,B两点为切点与抛物线相切的直线交于点P.设A,B的坐标分别为(x1,y1),(x2,y2),则

(1)切线PA的方程为y1y=p(x+x1),切线PB的方程为y2y=p(x+x2);

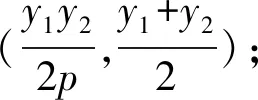
(3)直线AB的方程为(y1+y2)y-2px-y1y2=0;

(4)若点P的坐标为(x0,y0),则直线AB的方程为y0y-p(x+x0)=0;

(5)PA⊥PB,即切线PA与切线PB垂直;

(6)PF⊥AB;

(7)|PA|2=|AF|·|AB|,

|PB|2=|BF|·|AB|,

|PF|2=|AF|·|BF|;

(8)以AB为直径的圆与准线相切于点P,以AF为直径的圆与y轴相切,以BF为直径的圆与y轴相切;

(9)弦AB的中点与点P的连线与x轴平行,即弦AB的中点的纵坐标与点P的纵坐标相等;

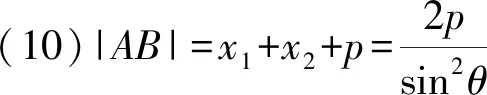
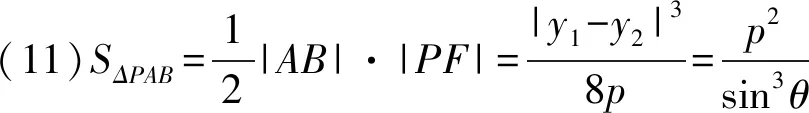
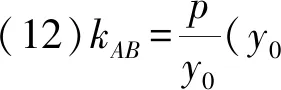
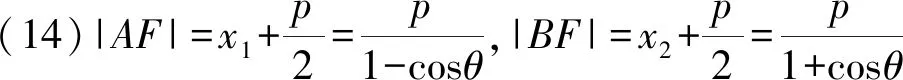
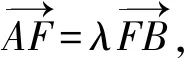
3 解法探究

设准线与x轴的交点为D.

根据阿基米德三角形的性质可知点P在准线上,如图1所示.

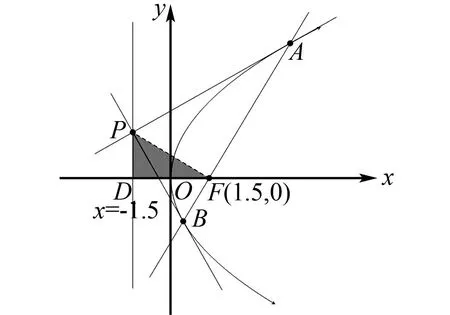
图1 试题图

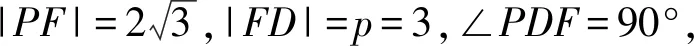
视角1[2]设A,B的坐标分别为(x1,y1),(x2,y2),由抛物线的切线性质得切线PA的方程为y1y=3(x+x1),切线PB的方程为y2y=3(x+x2).

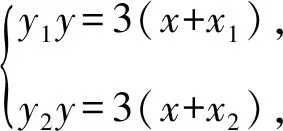
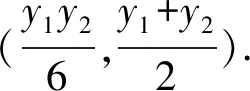
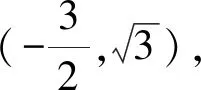
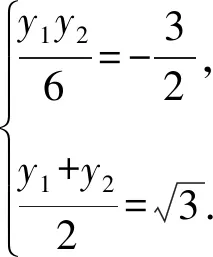
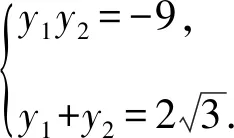
由抛物线的焦点弦的性质,得

|AB|=x1+x2+p

故选D.

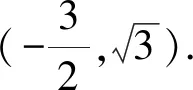
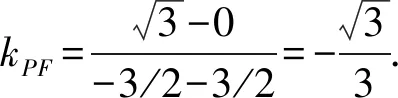
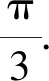
由抛物线的焦点弦的性质,得

故选D.

视角3设直线AB的倾斜角为θ.

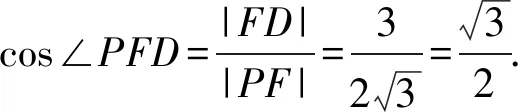
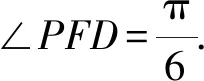
由阿基米德三角形的性质,得

由抛物线的焦点弦的性质,得

故选D.

视角4设弦AB中点的纵坐标为y0.

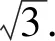
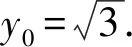
由抛物线的焦点弦的性质,得

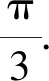
由抛物线的焦点弦的性质,得

故选D.

视角5弦AB中点的纵坐标为y0.

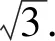
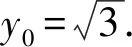
由抛物线的焦点弦的性质,得

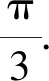
由抛物线的焦点弦的性质,得

所以|AB|=|AF|+|BF|=6+2=8.

故选D.

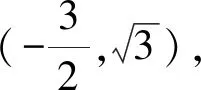
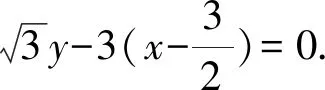
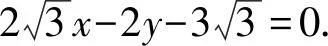
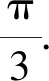
故选D.

视角7设A,B的坐标分别为(x1,y1),(x2,y2),

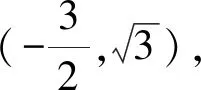
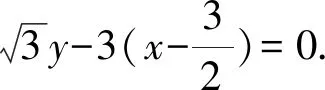
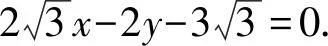
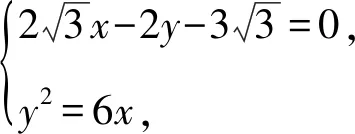
4x2-20x+9=0.

则x1+x2=5.

由抛物线的焦点弦的性质,得

|AB|=x1+x2+p=5+3=8.

故选D.

视角8设A,B的坐标分别为(x1,y1),(x2,y2),

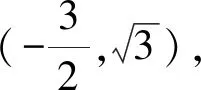
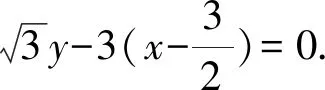
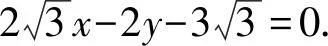
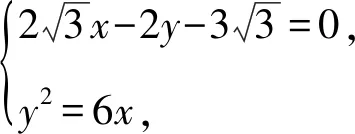
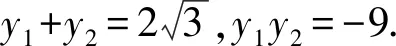
由弦长公式,得

故选D.

视角9由题意不妨设点A在第一象限,点B在第四象限,且坐标分别为(x1,y1),(x2,y2),

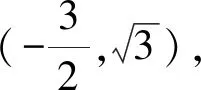
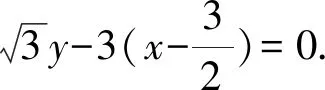
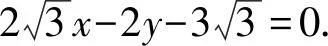
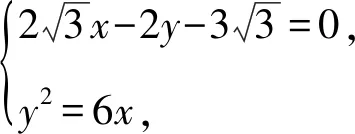
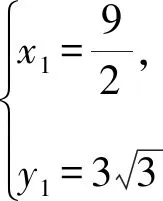
由两点间的距离公式,得

故选D.

视角10设A,B的坐标分别为(x1,y1),(x2,y2),

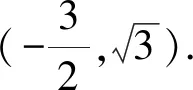
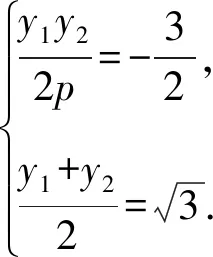
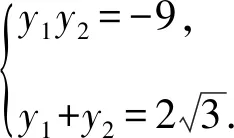
由抛物线的焦点弦的性质,得

|AB|=x1+x2+p

故选D.

视角11由题意不妨设点A在第一象限,点B在第四象限,且坐标分别为(x1,y1),(x2,y2).

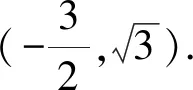
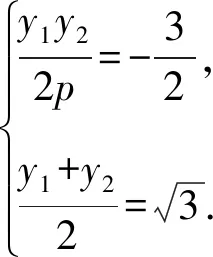
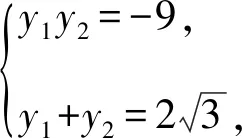
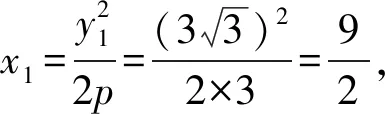
由抛物线的焦点弦的性质,得

故选D.

视角12由题意不妨设点A在第一象限,点B在第四象限,且坐标分别为(x1,y1),(x2,y2),

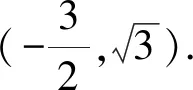
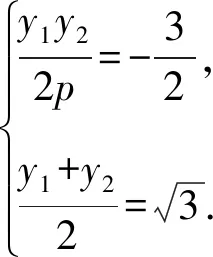
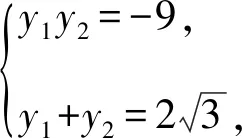
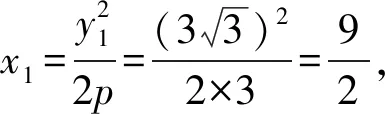
由两点间的距离公式,得

故选D.

视角13由题意不妨设点A在第一象限,点B在第四象限,且坐标分别为(x1,y1),(x2,y2).

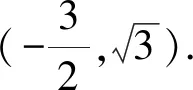
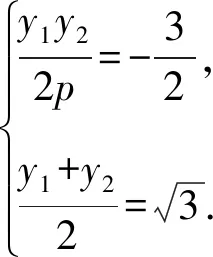
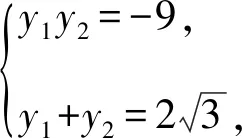
由阿基米德三角形的性质,得

由阿基米德三角形的性质,得

解得|AB|=8.

故选D.

视角14由阿基米德三角形的性质,抛物线的焦点弦的性质,得

解得|AB|=8.

故选D.

4 试题溯源

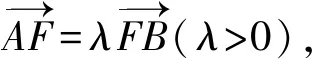
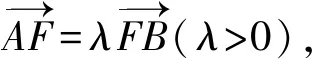
由阿基米德三角形的性质可知MF⊥AB.

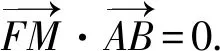
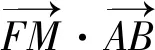
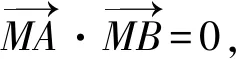
解析设AB中点的纵坐标为y0.

易知点M(-2,2)在抛物线的准线上.

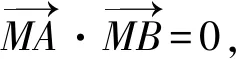
所以点M在以AB为直径的圆上.

由阿基米德三角形的性质可知点M(-2,2)是以AB为直径的圆与准线x=-2相切的切点,且线段AB中点的纵坐标为2.

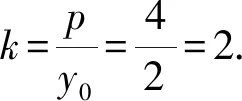
故选D.

题3 (2018年全国Ⅲ卷,理16)已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k=____.

解析易知点M(-1,1)在抛物线的准线上.

又因∠AMB=90°,则由阿基米德三角形的性质可知MF⊥AB.

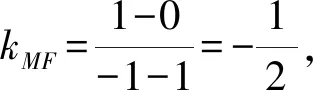
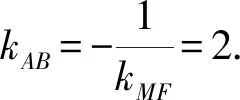
即直线AB的斜率k=2.

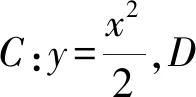
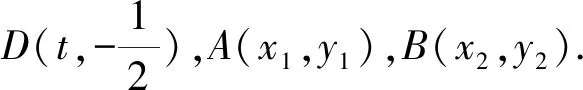
设直线AB的方程为y=kx+b,

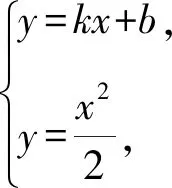
所以x1x2=-2b.

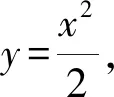
所以切线AD的方程为y-y1=x1(x-x1).

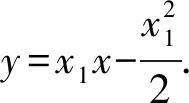
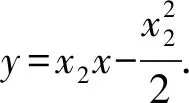
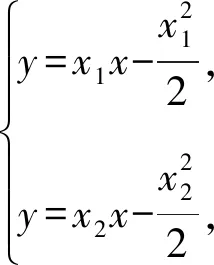
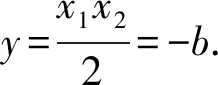
即点D的纵坐标为-b.

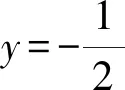
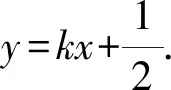
5 结束语

这道圆锥曲线问题以深刻的背景和清晰的表达,向我们呈现了一个图象鲜明、解法多样、层次多样的数学问题,本题深刻地、综合地考查了学生的直观想象、数学运算、逻辑推理等数学核心素养,有较大的难度.在平常的学习中,要特别注意对于背景结论的挖掘与反思,不能只停留在表面阶段,从几何到代数,再到运算,横向纵向多维度比较才能真正做到通一类、会一类,研究透彻一类数学问题.今后的教学应以数学问题为导向,深入挖掘,多面剖析,才能达到真正理解数学问题、提高数学能力的目的.