2023年“北大暑期学堂”数学试题及详解
李 艳
(北京市十一学校,北京100039)
2023年的测评分为两场:第一场为语文、数学、英语,总时长为3个半小时;第二场为两个选考科目,总时长为2个小时.其中,每一场都是所有考试科目的试卷一起发放一起收回,学生自行决定各科目的做题顺序以及时长;选考科目为物理、化学、历史、政治四个科目中选取两个科目,其中物理、历史必选其一.今年恢复了线下测评,因此数学试题也由去年的单项选择题改为了解答题.试题分文理科,每科都是5道题,每题20分,共100分,只要选择物理为选考科目的学生就考理科数学,其他学生考文科数学;文科和理科有3道题目是一样的,因此共有7道试题,本篇文章的前5道为文科数学试题,后5道为理科数学试题.
1 真题详解
题1(文科)在ΔABC中,过点A作∠B,∠C平分线的垂线,垂足分别为点D和点E,证明:DE∥BC.
解 析如图1,设∠B,∠C的平分线交于点I,且分别交AC,AB于点G,H,连接AI,则I为△ABC的内心,且AI平分∠A.
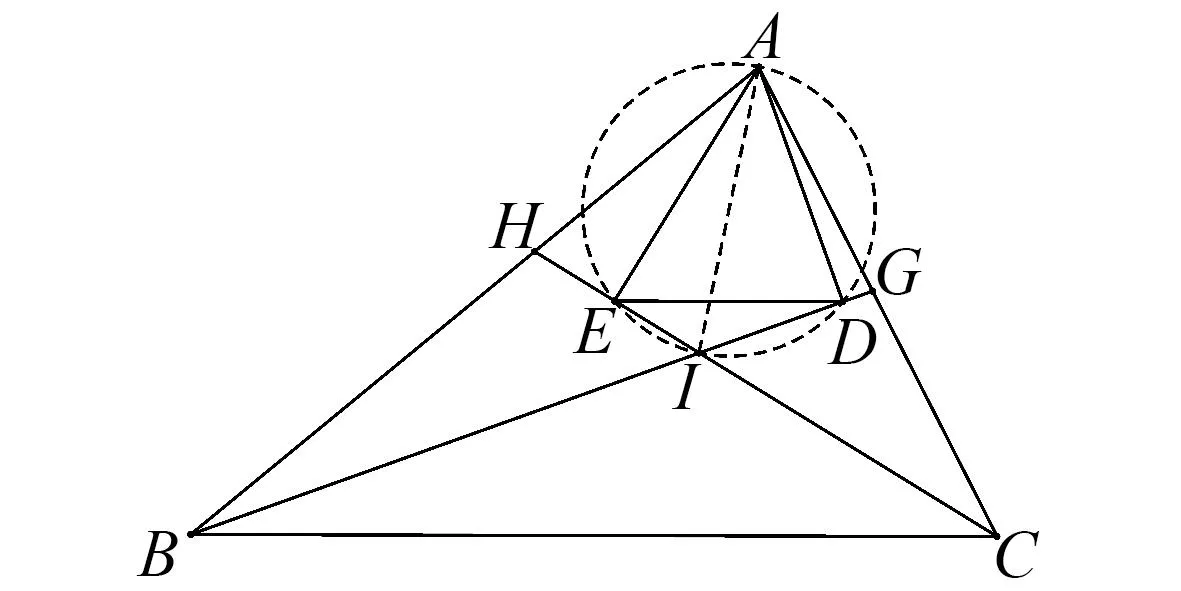
图1 题1解析图
因为AD⊥BD,AE⊥CE,所以A,D,I,E四点共圆.
所以∠DEI=∠IAD=90°-∠AID.
在△AIG中,∠AID=180°-∠IAG-∠AGI
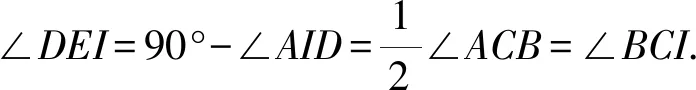
所以DE∥BC.(内错角相等,两直线平行)
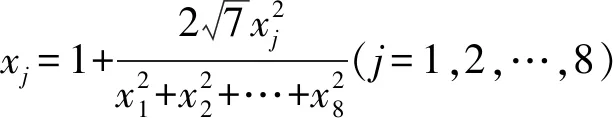
解析易知xj>1(j=1,2,…,8).
将已知的8个方程相加可得
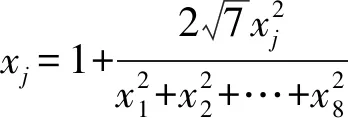
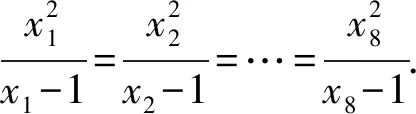
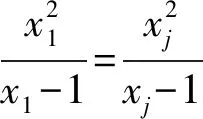
(x1-xj)(x1xj-x1-xj)=0(j=1,2,…,8).
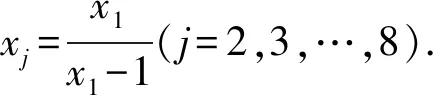
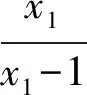
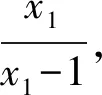
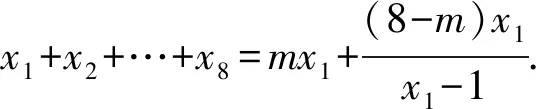
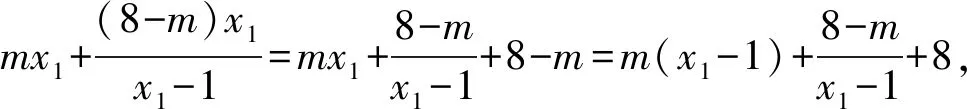
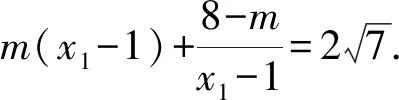
因为x1>1,由均值不等式可得
解得m≥7或m≤1,即m=1,7,8.
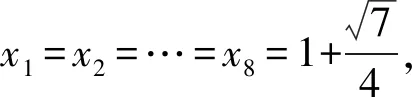
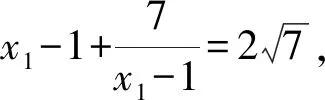
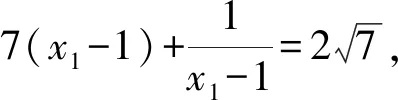
题3(文理科)设an=3(n2+n)+7,求数列{an}的前2 023项中为立方数的项的个数.
解析依题意,an≡1(mod3).
当k∈N*时,(3k)3≡0(mod3),(3k+1)3≡1(mod3),(3k+2)3≡2(mod3),
若an为某个数的立方,则有
an=(3k+1)3(k∈N*).
于是有3(n2+n)+7=27k3+27k2+9k+1.
即n2+n+2=9k3+9k2+3k.
若n≡0(mod3),则n2+n+2≡2(mod3);
若n≡1(mod3),则n2+n+2≡1(mod3);
若n≡2(mod3),则n2+n+2≡2(mod3).
综上可得n2+n+2≡1,2(mod3).
而9k3+9k2+3k≡0(mod3),故n2+n+2=9k3+9k2+3k不可能成立.
因此数列{an}的前2 023项中为立方数的项的个数为0.
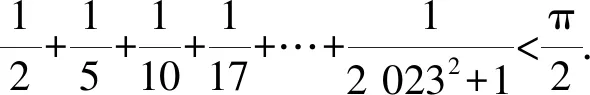
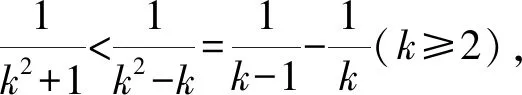
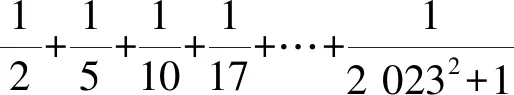
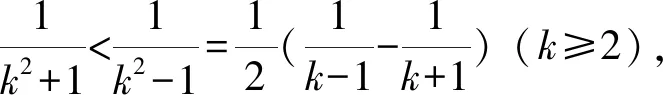
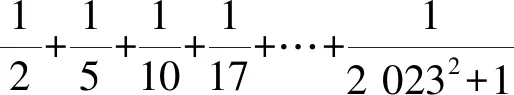
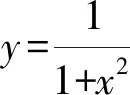
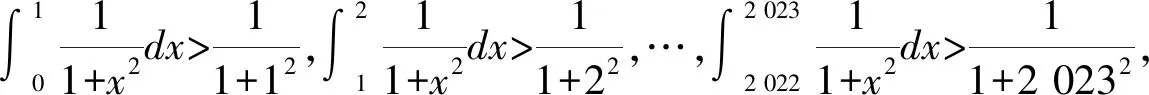
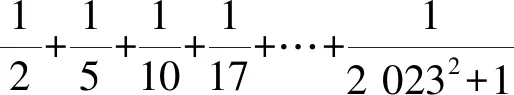
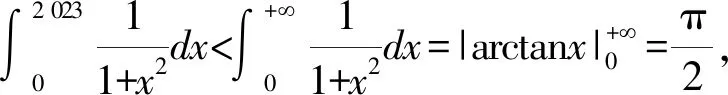
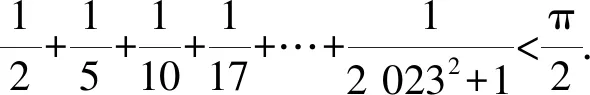
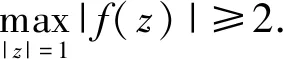
证明设f(z)=zn+an-1zn-1+…+a1z+1(ai∈C).
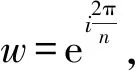
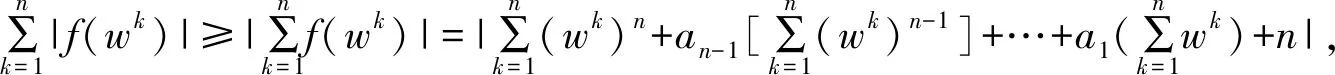
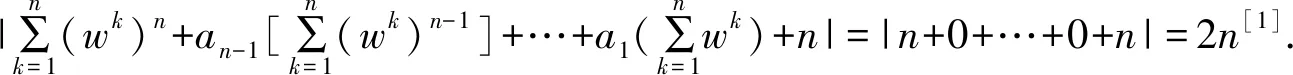
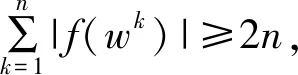
题6(理科)求由1,2,3,4,5,6六个数字构成的至少有三位数字不同且1,6不相邻的五位数个数.
解析1先算出来所有1,6不相邻的五位数个数,再减去只有1个数字和两个数字不同的且1,6不相邻的五位数的个数即可.
先考虑所有1,6不相邻的五位数的个数,分为以下几种情况:
(1)五位数中不包含1且不包含6:共有45=1 024个;
(2)五位数中只包含1或只包含6:共有
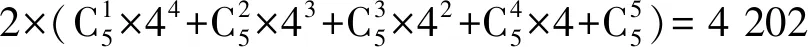
(按照这个五位数中有一个1,两个1,三个1,四个1,五个1进行分类)
(3)五位数中包含1且包含6:
若1和6共有三个,且1和6都至少有一个:共有42×3×3×2=288个;
若有一个1,三个6,或三个1,一个6:共有4×2×2=16个;
若1和6各有2个:共有4×2=8个[2];
综上可得,1,6不相邻的五位数的个数共有:
1 024+4 202+768+288+16+8=6 306个.
只有一个数字的五位数共有6个;
所以至少有三位数字不同且1,6不相邻的五位数个数共有
6 306-6-420=5 880个.
解析2设由1,2,3,4,5,6六个数字构成的且1,6不相邻的n位数个数为Sn,其中末位数字为1或6的有xn个,末位数字既不是1也不是6的共有yn个,于是有
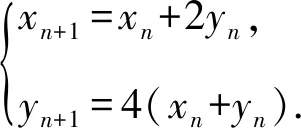
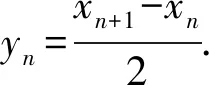
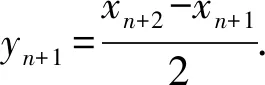
代入yn+1=4(xn+yn)中得
xn+2=5xn+1+4xn.
同理可得yn+2=5yn+1+4yn.
所以Sn+2=5Sn+1+4Sn,其中S1=6,S2=6×6-2=34.
所以S3=5×34+6×4=194,
S4=5×194+4×34=1 106,
S5=5×1 106+4×194=6 306.
所以1,6不相邻的五位数的个数共有6 306个.
以下同解析1.
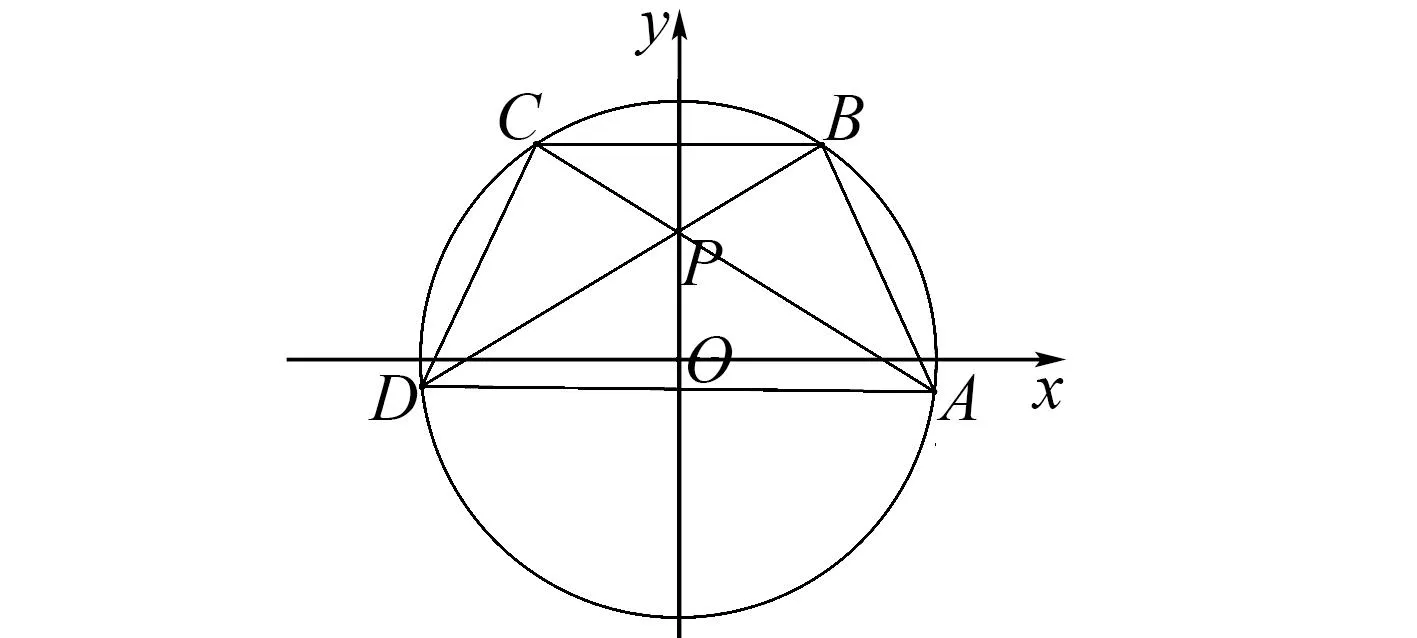
图2 题7解析图
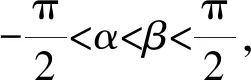
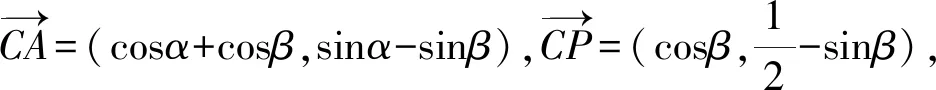
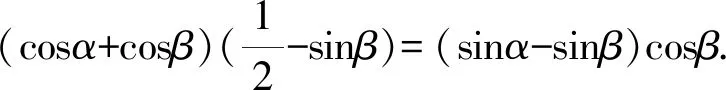
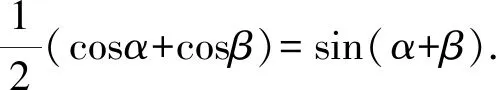
(*)
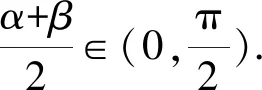
由(*)得
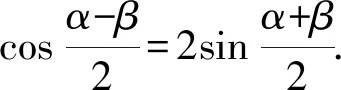
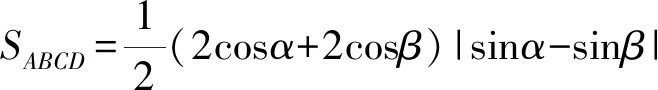
=(cosα+cosβ)(sinβ-sinα)
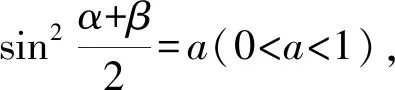
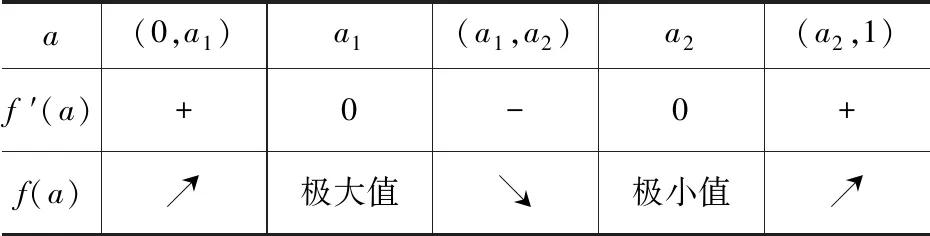
令f(a)=(1-a)2(1-4a)a(0 则f′(a)=-2(1-a)(1-4a)a-4(1-a)2a+(1-a)2(1-4a)=(1-a)(16a2-11a+1). 表1 f ′(a)和f(a)的变化情况表 因为f(1)=0, >0, 从内容来看,“北大暑期学堂”的考查内容是高中数学内容的延伸拓展,结合往年试题来看,出现比较多的模块是不等式与方程、平面几何、数论、计数、组合以及复数,并且对这些模块的知识考查比较深入灵活,超过了高考对这部分知识的考查要求.因此,想在“北大暑期学堂”的考试中取得不错的成绩还需要在平时学习中对这些知识模块的学习向深层次、揭示数学本质的过程转化[3].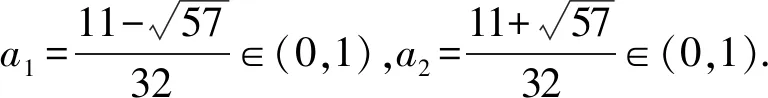
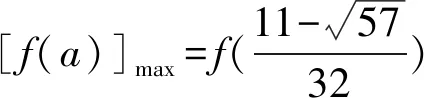
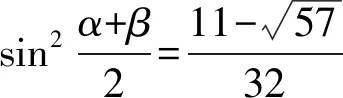
2 结束语

