坐标观点下的解析几何命题推广探究——以2023年全国乙卷理数第20题为例

金 毅

(呼和浩特市第二中学,内蒙古 呼和浩特 010000)

解析几何主要考查直观想象能力、逻辑推理能力与运算求解能力.坐标法是高中阶段解决解析几何问题的主要方法.“坐标法”的基本含义是:通过将几何关系转化为坐标,并使用代数方法对坐标进行运算,体现了解析几何中的数形结合思想[1].下面我们以2023年的一道高考题目为例,在坐标法的观点下研究其一般情形,并做推广.

1 题目呈现

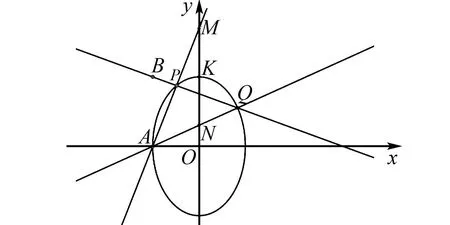
图1 全国乙卷理科数学20题

(1)求C的方程;

(2)过点(-2,3)的直线交C于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明:线段MN的中点为定点.

为了便于说明问题,不妨设点B(-2,3),M,N中点为K.本题充分考查学生的逻辑推理、直观想象和数学运算的核心素养,解决方法不唯一,可以多角度切入分析试题,定点结论简洁美观,是一道具备选拔功能的优秀试题,下面尝试对问题的一般化情况做讨论.

2 推广探究

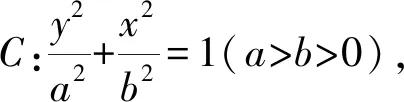
此结论证明方法较多.考虑到直线AP,AQ地位等同,知其运算方式是相似的.具体来看,当我们通过联立计算解决了点P的坐标时,点Q的坐标也可以通过类似的计算方式得出.所以,我们选择方程同构方法解决,目的是为了尽可能减少计算量.

证明设直线AP,AQ的方程分别为

y=k1(x+b),y=k2(x+b),

由韦达定理,可得

设直线PQ的方程为y-a=t(x+b),可得

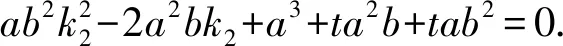
此时k1,k2可看作方程ab2x2-2a2bx+a3+ta2b+tab2=0的两个不等实数根.

对于直线AP,AQ,令x=0,可得

yP=bk1,yQ=bk2.

设MN的中点为K,

评注对于结论1,令a=3,b=2即得到乙卷理科第20题.通过此分析可以看到,几何上的相同地位暗示着相同的代数运算方式.事实上,我们证得定点的同时,发现本质上是斜率和为定值导致定点的出现,所以得到结论2.

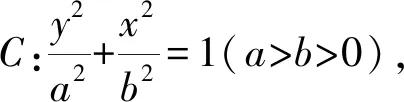
证明根据结论1,可得

故有kAP+kAQ=2kAK成立.

本结论可以推广至双曲线,于是得到结论3.

证明方法与结论1类似,此处略去.

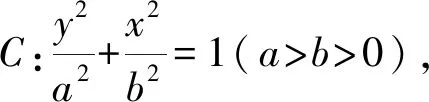
图2 结论4示意图

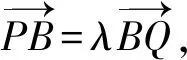
(-b-x1,a-y1)=λ(x2+b,y2-a).

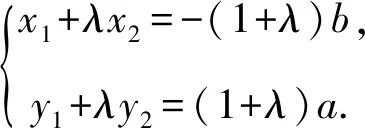
根据几何图形可知,λ≠-1.

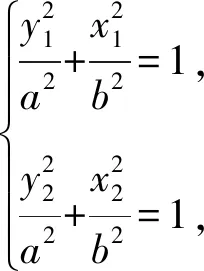
作差,得

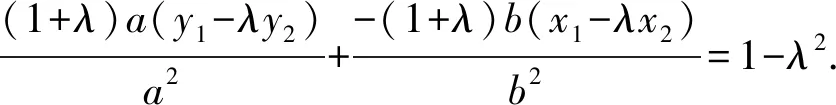
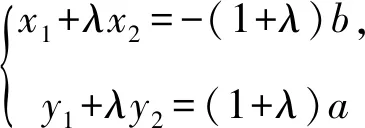
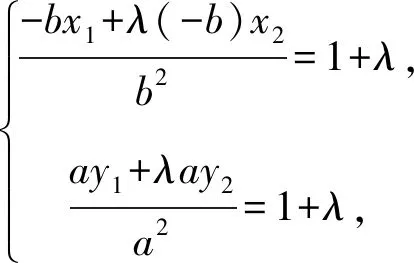
两者相加,可得

考虑表达式

①

②

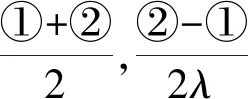
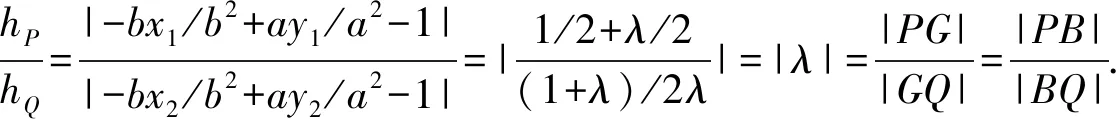
所以|PG|·|BQ|=|PB|·|GQ|.

评注我们用纯坐标法证明了此结论,避免了使用平面几何与高等几何中繁杂的推导,体现了坐标法的优势.若此结论成立,认为点B,P,G,Q为调和点列.在证明过程中,我们使用了定比点差法,点差法在代数结构上简明对称,便于我们找到等量关系,整体代换求出线段比为定值.事实上,此结论也揭示了全国乙卷20题的命题背景为调和点列.

结论4可一般化推广,我们得到结论5.

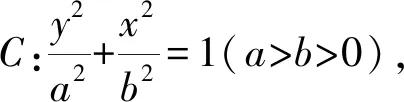
此结论的证明方式同结论4,并且对于焦点在x轴上的椭圆也成立.

调和点列的出现意味着出现调和线束,可知AB,AP,AG,AQ为调和线束.我们将调和点列的结论改进,得到结论6.

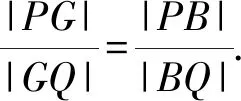
根据正弦定理,易证得

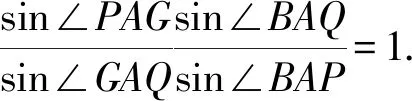
分别设调和线束AB,AP,AG,AQ的倾斜角为θ1,θ2,θ3,θ4,其斜率分别为k1,k2,k3,k4,根据三角形外角关系,得

有(k2-k3)(k1-k4)=(k3-k4)(k1-k2)成立.

也即(k2-k4+k4-k3)(k1-k4)=(k1-k4+k4-k2)(k3-k4).

即(k4-k3)(k1-k4)+(k2-k4)(k1-k4)=(k4-k2)(k3-k4)+(k1-k4)(k3-k4).

故有2(k1-k4)(k3-k4)=(k2-k4)(k1-k4)+(k2-k4)(k3-k4).

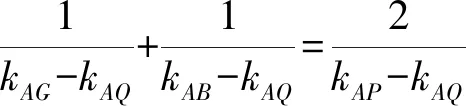
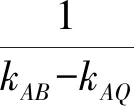
3 结束语

通过以上结论与分析可以看到,坐标法在解决解析几何问题时有非常重要的推动作用,能通过计算避免繁杂的几何推理,并且推导出来的结果更具备一般性.在运用坐标法计算时,要注意灵活运用代数中的对称、同构、替换的思路,巧妙运算,减少计算量.同时,解析几何的关系经过坐标的加工、转化之后可以出现新的数学问题.正是坐标观点的出现,使解析几何问题的呈现形式多样化,变得越来越丰富多彩,引人入胜.