高考数学复习备考策略的研究
——以2023年全国卷高考数学试题为例
董同明
(江苏省东海高级中学,江苏 连云港 222300)
1 数学复习要强调基础性
深化基础考查是高考数学命题的根本,虽然高考数学试题千变万化,但不变的是数学的基础知识、基本技能和基本思想方法.

A.-i B.i C.0 D.1
试题分析本题考查复数的代数形式、复数代数形式的运算、共轭复数的概念等基础知识和基本方法.由题意首先计算复数z的值,然后利用共轭复数的定义确定其共轭复数即可.
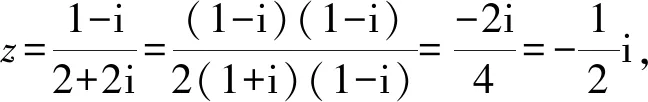

故选A.
2 数学复习要突出综合性
作为选拔性考试的高考,综合性就成为高考数学命题的重要特征.高考数学命题依据课程标准,落实“综合性”考查要求,彰显学科核心素养,突出对主干、重点知识、内容及关键能力的考查,考查综合应用知识的能力.高考复习备考要重视知识点的交叉,学会从一个知识点向另一个知识点转化的方法,即转化条件、转化结论.学会在不同的知识点之间建立起桥梁,学会对各个知识点进行挖掘、扩展,既深入思考又广开思路,这是复习备考的核心问题.
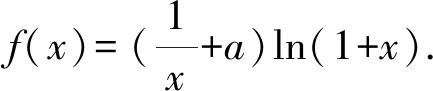
(1)当a=-1时,求曲线y=f(x)在点(1,f(1))处的切线方程;

(3)若f(x)在(0,+∞)上存在极值,求a的取值范围.
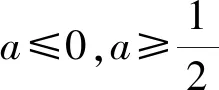
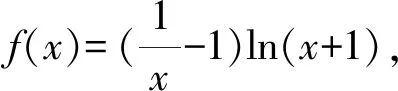
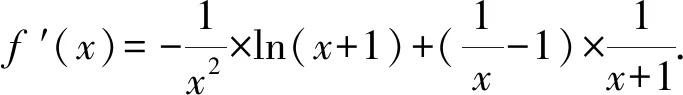
据此可得f(1)=0,f′(1)=-ln2.
函数在(1,f(1))处的切线方程为
y-0=-ln2(x-1).
即xln2+y-ln2=0.
(2)由函数的解析式可得
由对称性可知

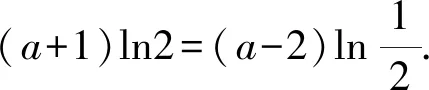
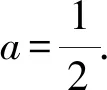
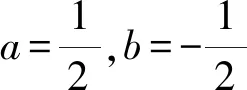

(3)由函数的解析式可得
由f(x)在区间(0,+∞)上存在极值点,则f′(x)在区间(0,+∞)上存在变号零点.

-(x+1)ln(x+1)+(x+ax2)=0.
令g(x)=ax2+x-(x+1)ln(x+1),
f(x)在区间(0,+∞)存在极值点,等价于g(x)在区间(0,+∞)上存在变号零点,
当a≤0时,g′(x)<0,g(x)在区间(0,+∞)上单调递减,此时g(x) 令m(x)=1-x+lnx(0 所以函数m(x)在定义域内单调递增.所以m(x) 令h(x)=lnx-x2+x(x>0),则 当x∈(0,1)时,h′(x)>0,h(x)单调递增,当x∈(1,+∞)时,h′(x)<0,h(x)单调递减,故h(x)≤h(1)=0. 即lnx≤x2-x(取等条件为x=1). 所以g′(x)=2ax-ln(x+1)>2ax-[(x+1)2-(x+1)]=2ax-(x2+x), g′(2a-1)>2a(2a-1)-[(2a-1)2+(2a-1)]=0,且注意到g′(0)=0. 根据零点存在性定理可知:g′(x)在区间(0,+∞)上存在唯一零点x0. 当x∈(0,x0)时,g′(x)<0,g(x)单调递减,当x∈(x0,+∞)时,g′(x)>0,g(x)单调递增,所以g(x0) 所以g(x)=ax2+x-(x+1)ln(x+1) 所以函数g(x)在区间(0,+∞)上存在变号零点,符合题意. 数学应用已经渗透到现代社会及人们日常生活的各个方面,而应用数学解决问题是学生学科核心素养的综合体现.数学模型搭建了数学与外部世界联系的桥梁,是数学应用的重要形式.因此,高考命题重视应用数学模型解决实际问题,强化对“应用意识”的考查,既体现课程标准的要求,也是考查学生学科素养的重要手段. 例3(新高考Ⅱ卷第19题)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如图1所示的患病者和未患病者该指标的频率分布直方图: 图1 频率分布直方图 利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为p(c);误诊率是将未患病者判定为阳性的概率,记为q(c).假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率. (1)当漏诊率p(c)=0.5%时,求临界值c和误诊率q(c); (2)设函数f(c)=p(c)+q(c),当c∈[95,105]时,求f(c)的解析式,并求f(c)在区间[95,105]的最小值. 试题分析(1)根据题意由第一个图可先求出c,再根据第二个图求出c≥97.5的矩形面积即可解出; (2)根据题意确定分段点100,即可得出f(c)的解析式,再根据分段函数的最值求法即可解出. 解析(1)根据题意可知,左边图形第一个小矩形的面积为5×0.002>0.5%,所以95 q(c)=0.01×(97.5-95)+5×0.002=0.035=3.5%. (2)当c∈[95,100]时,f(c)=p(c)+q(c)=(c-95)×0.002+(100-c)×0.01+5×0.002=-0.008c+0.82≥0.02; 当c∈(100,105]时,f(c)=p(c)+q(c)=5×0.002+(c-100)×0.012+(105-c)×0.002=0.01c-0.98>0.02. 故f(c)在区间[95,105]的最小值为0.02. 培养学生的创新精神、创新意识和创新能力是高中数学新课程的重要任务,而在数学探究中发现问题、提出问题,并应用数学知识、思想方法分析问题和解决问题是这种创新性的最好表现.高考命题重视对情境创新性的考查,这就要求我们在高考复习备考中重视和加强对数学创新型问题的研究,并引导学生加强对创新问题的训练,以适应高考命题的要求. 试题分析根据直线与圆的位置关系,求出弦长|AB|,以及点C到直线AB的距离,结合面积公式即可解出. 教育部考试中心发布的高考评价体系由“一核”“四层”“四翼”组成,其中:“四翼”即基础性、综合性、应用性、创新性为考查要求[1].高考数学复习备考要强化对实现“四翼”考查要求策略的研究,把复习备考的着眼点放在数学的“问题本质”和能力培养上,将本质性的东西弄熟吃透了,阅读理解能力及数学抽象、逻辑推理和数据分析、直观想象和数学建模等数学核心素养提高了,相应的问题便迎刃而解.


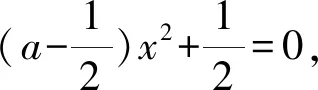
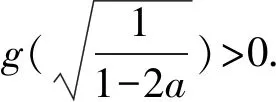
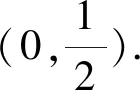
3 数学复习要关注应用性

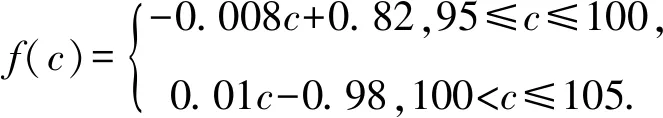
4 数学复习要重视创新性
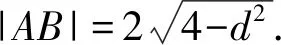
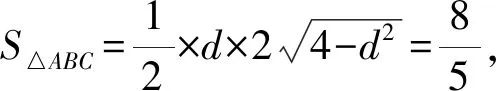
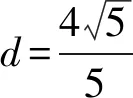



5 结束语

